|
|
|
LUMINI SI UMBRE IN COSMOS - Obiectul luminat de o singura sursa a. Umbre multiple
Sa consideram, mai intai, cazul unui corp (sferic) luminat de doua surse punctiforme.
Figura
1.17
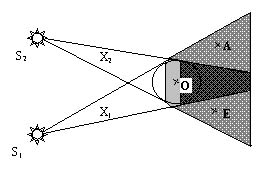
Figura 1.17 ne da o imagine a situatiei, reprezentata, pentru simplitate, in planul determinat de sursele S1, S2 si centrul O al corpului sferic dat.
Se vede ca fiecarei surse ii corespunde un 'con de umbra', dar aceste conuri nu mai sunt, in intregime, conuri 'de intuneric'! Intr-adevar, punctul A, aflat in 'conul de umbra' x1, primeste totusi lumina de la sursa S2, fiind lipsit numai de lumina sursei S1. Asemanator se petrec lucrurile si in punctele din conul x2, (de ex., punctul E).
Ne dam seama imediat ca intuneric deplin este doar in domeniul care apartine simultan conurilor x1 si x2 (portiunea dublu hasurata din fig. 1.17). in restul celor doua conuri nu avem de a face cu o umbra propriu-zisa ci cu o umbra atenuata de lumina unei alte surse.
Rezulta ca un corp iluminat de doua surse punctiforme de lumina creaza doua conuri de umbra atenuata; intersectia acestor conuri da nastere unui con de umbra propriu-zisa pentru corpul respectiv.
Ce se intampla, in acest caz, cu umbra corpului? Ea va depinde, in mod esential, de locul unde se plaseaza ecranul pe care se 'creeaza' umbra si, de regula, nu avem o singura umbra ci doua, dar ambele sunt 'umbre atenuate'.
Gradul de atenuare depinde de intensitatile celor doua surse; metoda iluminarii cu mai multe surse este utilizata in situatiile in care umbrele nete (propriu-zise) sunt suparatoare; exemplele cele mai frecvente le intalnim in lumea spectacolelor - pe scena teatrului sau in studiourile de film si televiziune.
Lasam in seama cititorului sa studieze diferite configuratii ale umbrelor multiple (atenuate) pe ecrane plasate in diferite pozitii si pentru diferite asezari ale surselor si ale obiectului iluminat. Reintorcandu-ne la situatia redata in figura 1.17, mai retinem faptul ca:
Din interiorul conului de umbra nu poate fi vazuta nici una din surse, ambele fiind ocultate de obiect;
Din punctele aflate intr-unul din conurile de umbra atenuata se poate vedea doar una din surse, cealalta fiind ocultata de obiect.
Sa mai analizam un aspect: in figura 1.17, distanta dintre surse este mai mare decat diametrul corpului luminat; ne dam seama usor ca, daca distanta dintre surse scade, conul de umbra este tot mai lung. Daca distanta dintre cele doua surse este egala cu diametrul corpului, atunci generatoarele conului de umbra devin paralele, iar conul de umbra se alungeste la nesfarsit, transformandu-se intr-un cilindru de umbra. in sfarsit, daca distanta dintre surse este mai mica decat diametrul corpului, conul de mbra devine divergent, astfel incat umbra se va obtine, inconjurata de umbra (sau lumina, daca preferam) atenuata, la orice distanta de corp, in partea opusa surselor.
Cititorul poate analiza singur, pe baza acelorasi principii geometrice simple, multe alte situatii in care intervin surse punctuale: cazul a mai mult de doua surse, cazuri in care sursele nu ne afla toate la aceeasi distanta de obiect, cazuri in care sursele nu au toate aceeasi intensitate luminoasa etc..
b. Penumbra
Ce se intampla daca avem - din nou - o singura sursa, dar aceasta nu este punctiforma? intrebarea noastra este justificata de faptul ca, intr-adevar, in multe cazuri, nu mai putem face abstractie de dimensiunile surselor luminoase (de exemplu, in cazul tuburilor fluorescente, in cazul Soarelui etc.).
Vom cauta sa reducem cazul surselor cu dimensiuni apreciabile la cazul producerii umbrelor prin iluminarea cu surse punctuale, considerand ca orice punct de pe suprafata sursei date se comporta ca o sursa punctuala independenta.
Evident, nu putem construi conurile de umbra atenuata ale tuturor punctelor sursei, acestea fiind in numar infinit; vom cauta numai sa delimitam zona din spatiu unde nu poate ajunge nici o raza luminoasa, precum si zona in care pot ajunge unele, dar nu toate razele luminoase pornite din punctele sursei. Prima din aceste zone este zona de umbra a corpului, iar cea de a doua se mai numeste 'zona de penumbra'.
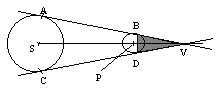Figura1.18
Vom analiza cazul cel mai simplu, al unui corp opac sferic luminat de o sursa sferica; in practica, acesta este cazul planetelor si al satelitilor din sistemul solar, care primesc lumina de la Soare. Cu gandul la aceste corpuri, vom lua sursa mai mare decat obiectul opac, Soarele fiind mult mai mare decat orice alt corp din sistemul solar. Reprezentam mersul razelor de lumina doar intr-un plan oarecare ce trece prin centrele celor doua sfere (fig. 1.18); evident, in oricare din aceste plane situatia este aceeasi.
Sa cautam, mai intai, conul de umbra al corpului; pentru aceasta, 'mergem' pe axa centrelor (dreapta SP), de la punctul P, spre partea opusa lui S. Primele puncte prin care 'trecem' nu primesc nici o raza de lumina din vreun punct al sursei; ultimul punct in care nu ajunge nici o raza de lumina este punctul V, in care se intalnesc tangentele comune 'exterioare' (AB si CD) ale celor doua sfere. Mai mult, dupa ce trasam aceste tangente, putem verifica usor ca in nici un punct al 'domeniului' VBD nu poate patrunde nici o raza de lumina! Am gasit sectiunea axiala a conului de umbra (triunghiul VBD)
Pentru a localiza penumbra, vom proceda oarecum 'indirect': cautam sa delimitam zonele formate din puncte in care iluminarea nu este diminuata deloc, adica din puncte in care pot ajunge raze luminoase provenite de oriunde de pe sursa. Evident, o astfel de zona trebuie sa cuprinda intreaga sursa, dar sa nu includa nici o portiune din corpul opac.
Figura
1.19
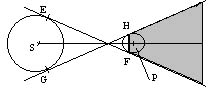
O astfel de impartire a planului figurii (fig. 1.19) se poate face printr-o dreapta care sa fie tangenta la ambele corpuri, dar sa lase sursa de o parte, iar corpul opac de cealalta parte a ei; este vorba, evident, de fiecare din tangentele comune 'interioare' ale celor doua corpuri (EF si GH). Portiunea hasurata din fig. 1.19 reprezinta, deci, sectiunea axiala a conului de penumbra; se verifica imediat (grafic) ca, pentru orice punct din aceasta zona, exista raze luminoase care nu pot 'patrunde' pana acolo.
Figura
1.20
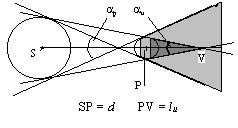
Reunind cele doua reprezentari, obtinem, in figura 1.20, imaginea conurilor de umbra si de penumbra in cazul unei surse luminoase sferice si a unui corp opac sferic.
Se poate remarca faptul ca, pentru doua corpuri date (unul luminos si celalalt opac), configuratia conurilor este mereu aceeasi, nedepinzand de distanta dintre corpuri. Distanta dintre corpuri influenteaza doar gradul de 'alungire' al conurilor, adica unghiurile din varfurile conurilor de umbra si de penumbra. Cititorul poate verifica singur aceasta, pastrand constante dimensiunile corpurilor si luand diferite distante intre sursa si obiect.
Relatiile care exista intre razele Rs si Rc ale celor doua corpuri (Soare si obiect), distanta dintre centre si caracteristicile conurilor de umbra si penumbra se pot deduce pe baza triunghiurilor din figura 1.20. Cu notatiile din aceasta figura, se obtin imediat: lungimea conului de umbra (lu), unghiul conului de umbra (a u) si unghiul conului de penumbra (a p):
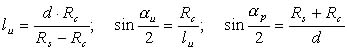Formula (1.26)
c. Probleme
Problema 1.2.3. Sa se determine forma terminatorului unui obiect sferic luminat de doua surse punctuale identice, aflate la distante egale de obiect.
Problema 1.2.4. in ce conditii terminatorul unui obiect nu exista?
Problema 1.2.5. Sa se construiasca conurile de umbra si de penumbra ale unui obiect sferic de raza mai mare decat a sursei (sferice) care il lumineaza.
