
|
|
|
GIROCOMPASUL1
1.1. Generalitati. Definitii.
Girocompasul este unul2 dintre aparatele de navigatie folosite pentru determinarea cursului3 navei.
Functionarea acestui aparat se bazeaza pe exploatarea celor doua proprietati fundamentale ale giroscopului cu trei grade de libertate (§1.3), inertia (§1.5) si precesia (§1.7).
Giroscopul cu trei grade de libertate este un sistem format dintr-un rotor (tor giroscopic) si o suspensie care asigura un punct fix pe axa de simetrie a rotorului.
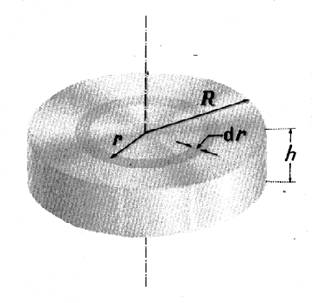
pentru calculul momentului de inertie al unui cilindru plin
R - raza cilindrului plin
r - raza stratului inelar
dr - grosimea stratului inelar
h - inaltimea cilindrului
![]()
1 - este cunoscut si sub denumirea de compas giroscopic.
2 - pentru orientarea pe mare, se mai foloseste, dar cu erori mult mai mari, compasul magnetic. Din punct de vedere cronologic, compasul magnetic a fost utilizat inainte de aparitia girocompasului.
3 - termen folosit in navigatia maritima (in limba engleza heading); exprima simultan atat directia cat si sensul de deplasare al navei. Se foloseste frecvent termenul marinaresc drumul navei.

1.2. Momentul de inertie al torului giroscopic
J = r2 dm (1.0)
unde:dm este masa elementului de volum4 situat la distanta
r fata de axa de simetrie (fig.G1), iar
dm = 2prhr dr
unde:h este inaltimea cilindrului avand densitatea
r uniforma, rezultand:
R
4
![]() J = 2prh r3 dr = 2prh R4
J = 2prh r3 dr = 2prh R4
0
1 2
![]() adica: J = mR2(1.1)
adica: J = mR2(1.1)
momentul de inertie al torului giroscopic ideal5 este evident:
J = mR2(1.2)
adica de doua ori mai mare decat al cilindrului plin.
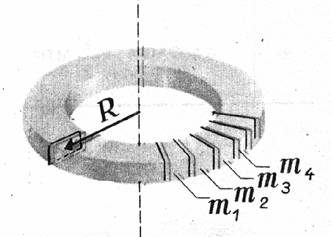
Intr-adevar, momentul de inertie al unui inel subtire, de masa m si raza medie R fata de axa sa, se poate calcula impartind inelul in n segmente, fiecare la distanta R fata de axa (fig.G2), obtinand:
i = n
i = 1
adica: J = mR2(q.e.d.)
![]()
4 - elementul de volum se alege sub forma unui strat inelar de grosime dr (fig.G1).
5 - torul giroscopic ideal este de forma unui strat inelar de grosime infinitezimala, de raza R si inaltime h, incarcat cu o masa apreciabila m (se poate imagina un cilindru gol avand aceeasi raza, aceeasi inaltime si a carui aceeasi masa m este continuta numai de suprafata sa cilindrica laterala - masa este repartizata la periferia cilindrului)
R - raza medie a torului mi - masa elementara
Fig.G2
Din motive care tin de limitarile tehnologice actuale, constructia rotorului giro nu este chiar de forma torului giroscopic ideal, ci una ca cea prezentata in figura G3, in care masa principala6 (masa torului propriu-zis) este concentrata spre periferie, in raport cu axa de simetrie a rotorului.
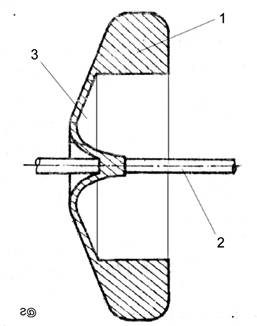

6 - masa secundara este mult mai mica decat cea a intregului rotor si este continuta de "fusta" sustinatoare a torului giroscopic.
1.3. Gradele de libertate ale rotorului giroscopic
Pentru a-i putea exploata principalele proprietati, inertia si precesia, rotorului giroscopic i se da numai posibilitatea de efectuare a miscarilor de rotatie in jurul celor trei axe de coordonate. Astfel numarul gradelor de libertate este N = 3 (fig.G4a, b), adica:
torul se poate roti liber in jurul axei de simetrie x - x', axa principala (de rotatie proprie) a giroscopului;
torul isi poate modifica zenitul, rotindu-se in jurul axei y -y';
torul isi poate modifica azimutul, rotindu-se in jurul axei z - z'
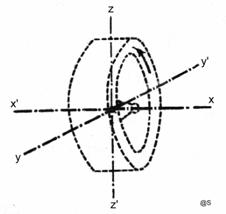
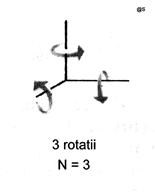
a) b)
fig.G4
Originea sistemului de axe de coordonate se numeste, in acest caz, centrul giroscopului si este in acelasi timp centrul de masa (greutate) al rotorului giro.
1.4. Suspensia giroscopului cu trei grade de libertate
In principiu, suspensia este asigurata de un sistem cardanic care consta in doua elemente mobile:
- elementul cardanic orizontal, care se poate roti in jurul axei y - y'
- elementul cardanic vertical, care se poate roti in jurul axei z - z'.
Miscarea principala de rotatie (engl: spin rotation) este posibila datorita existentei unei perechi de lagare, continute de elementul cardanic orizontal, in care se poate roti cu frecari neglijabile, axul rotorului giro.
Miscarea de rotatie in jurul axei y - y', fata de orizontul adevarat al locului (engl: tilt rotation), este posibila datorita unei alte perechi de lagare continute de elementul cardanic vertical, in care se poate roti elementul cardanic orizontal.
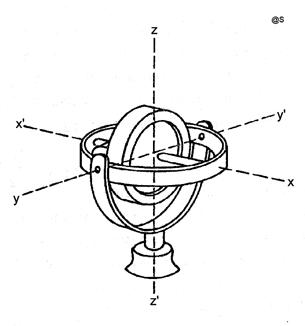
Miscarea de rotatie in jurul axei z - z', fata de meridianul adevarat al locului, (engl: heading rotation) este posibila datorita lagarelor (fig.G6) sau lagarului (fig.G7) din suportul suspensiei cardanice.
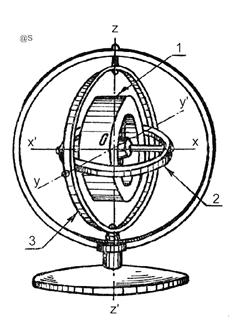 |

Ambele variante de suspensie cardanica ofera acelasi numar de grade de libertate (N = 3), permitand miscari de rotatie in jurul celor trei axe de coordonate.

1.5. Momentul cinetic al giroscopului
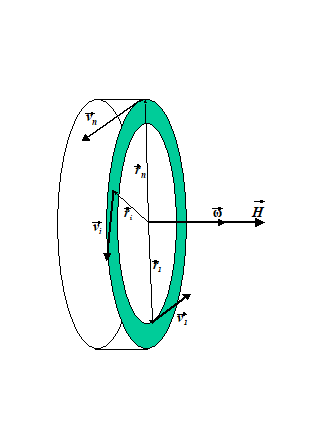
Fiecare particula de masa mi, situata la distanta ri de axa principala de rotatie (fig.G8), are viteza liniara vi, tangenta la traiectoria circulara de raza ri, incat momentul cinetic al giroscopului este:
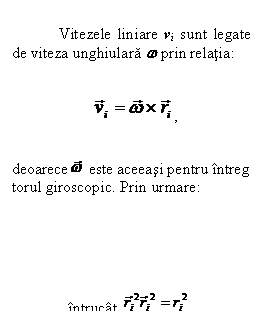
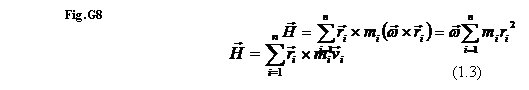
Introducand momentul de inertie definit prin relatia (1.2), rezulta:
![]() (1.4)
(1.4)
1.6. Inertia giroscopului
Legea inertiei afirma ca in lipsa vreunei interactiuni, un corp solid rigid isi pastreaza momentul impulsului (cinetic), adica:
![]() (1.5)
(1.5)
In cazul unui giroscop liber, aceasta inseamna
ca produsul ![]() ramane constant,
sub conditia ca valoarea vitezei unghiulare sa ramana
constanta, suportul vectorului
ramane constant,
sub conditia ca valoarea vitezei unghiulare sa ramana
constanta, suportul vectorului ![]() pastrandu-si
neschimbata directia in spatiu.
pastrandu-si
neschimbata directia in spatiu.
Asadar, torul giroscopic caruia i s-a imprimat o viteza unghiulara considerabila si constanta, isi mentine axa principala de rotatie paralela cu ea insasi, indicand aceeasi directie in spatiu.
Observatia este valabila daca asupra giroscopului cu trei grade de libertate nu actioneaza nici o forta avand un suport exterior centrului giroscopului.
Proprietatea poarta numele de inertie giroscopica.
Aceasta proprietate face ca axa principala a giroscopului, care are de fapt o pozitie invariabila in spatiu, sa prezinte o miscare aparenta fata de reperele terestre, din cauza miscarii diurne a Pamantului.
1.6.1. Miscarea aparenta a giroscopului aflat la polii terestri
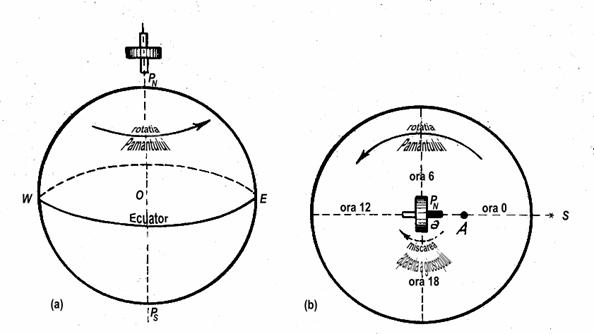
In fig.G9(a) axa principala de rotatie a giroscopului este continuta in axa de rotatie a Pamantului si nu efectueaza nici o miscare aparenta, pentru un observator terestru.
Daca axa principala a giroscopului aflat la pol este orizontala pentru observator si orientata initial spre astrul S (fig.G9-b), capatul a va descrie, in 24 ore siderale, in raport cu punctul A de pe Pamant, o rotatie completa (360 ) in sens invers trigonometric.
![]()
Fig.G9. Miscarea aparenta a giroscopului aflat la Polul Nord
1.6.2. Miscarea aparenta la Ecuator (fig.G10)
Axa principala a giroscopului este in momentul initial paralela cu orizontul si orientata pe directia N-S (a). Deoarece axa giroscopului este paralela cu axa Pamantului, acest paralelism se va mentine de-a lungul celor 24h ale rotatiei terestre complete si in tot acest timp nu se va observa nici o miscare aparenta a giroscopului. Axa ramane in meridianul locului, paralela cu orizontul.
In cazul (b) axa principala a giroscopului este, la momentul t = 0h, paralela cu orizontul, insa orientata pe directia E-W, deci perpendiculara pe planul meridianului si pe axa terestra. Pentru observatorul de la fata locului, capatul a se ridica treptat deasupra orizontului, iar dupa 6h ajunge la zenit. La momentul t =12h, axa principala devine iarasi paralela cu orizontul, insa avand capatul a orientat spre vest. Dupa inca 6h capatul a se afla orientat spre centrul Pamantului (axa principala este iarasi paralela cu axa terestra).
La momentul t = 24h, giroscopul se afla in pozitia initiala, avand executata o miscare aparenta (c) de 360 intr-un plan perpendicular pe planul meridianului locului.
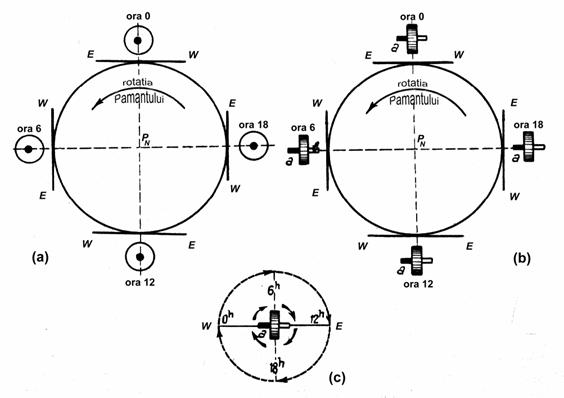
Fig.G10 Miscarea aparenta a giroscopului la Ecuator
1.6.3. Miscarea aparenta a giroscopului la o latitudine oarecare
Giroscopul si observatorul se gasesc la o latitudine oarecare j, iar axa principala este paralela cu orizontul si orientata pe directia N-S, la momentul t = 0 (fig.G11). In felul acesta, axa principala face cu axa Pamantului, la momentul initial, un unghi de valoare egala cu latitudinea (j
Odata cu rotirea Pamantului de la vest spre est, are loc si rotirea planului meridianului si a planului orizontului locului. Are loc in acest fel, o miscare aparenta a axei principale de rotatie a giroscopului - capatul a se deplaseaza spre dreapta meridianului (spre est) si se ridica deasupra orizontului. La momentul t = 6h, axa principala va face unghiul a cu directia N-S si unghiul j atat cu planul meridianului, cat si cu planul orizontului. La t = 12h, axa principala se gaseste din nou in meridian, dar sub un unghi de 2j fata de planul orizontului. La t = 18h, axa principala ocupa o pozitie simetrica fata de cea avuta la t = 6h.
Axa principala a giroscopului descrie deci, un unghi solid cu valoarea 2j

Fig.G11 Miscarea aparenta a giroscopului la o latitudine oarecare
1.7. Precesia giroscopului
Definitie: Polul giroscopului este un punct de pe axa principala de rotatie, din care rotirea torului se observa in sens trigonometric (fig.G12).
Daca asupra axei principale a giroscopului se aplica o forta exterioara F oarecare, axa principala se va roti intr-un plan perpendicular pe suportul fortei, sensul miscarii fiind dat de regula burghiului drept. Aceasta miscare poarta numele de miscare de precesie.
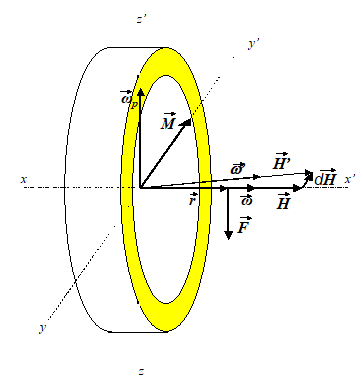
Fig.G12 Precesia giroscopului
Daca se lasa sa actioneze un moment exterior M, de exemplu prin atarnarea unei greutati de masa m la distanta r de punctul de suspensie, atunci:
![]() (1.6)
(1.6)
iar giroscopul (varful vectorului se roteste intr-un plan perpendicular pe suportul fortei F. Fenomenul poarta denumirea de precesie regulata; cauza acestei precesii este continuta in teorema momentului cinetic (1.7) conform careia actiunea momentului unei forte al carei suport nu contine centrul geometric si de masa al giroscopului, produce o variatie in timp a momentului cinetic:
![]() (1.7)
(1.7)
Variatia dH se produce pe directia momentului M al fortei F, adica perpendicular pe suportul vectorului moment cinetic H. In intervalul de timp dt, vectorul moment cinetic se roteste cu unghiul:
![]() (1.8)
(1.8)
catre H' (fig.G12), avand loc miscarea de precesie a giroscopului.
Pentru viteza unghiulara a precesiei:
![]()
rezulta din (1.8) si (1.4 - H = J):
![]() (1.9)
(1.9)
in scriere vectoriala:
![]()
Observatie:
Relatia (1.9) este valabila numai atat timp cat >>p; in caz contrar, viteza unghiulara rezultanta nu mai are directia lui H, astfel ca nu mai poate fi folosita relatia (1.4). Cand devine prea mica, miscarea de precesie devine instabila.
Daca asupra unui giroscop nesupus actiunii vreunei alte forte, se exercita un moment de rotatie M de durata, cu directie constanta (diferit de fig.G12, unde directia momentului fortei se roteste impreuna cu precesia), atunci, conform (1.7), H este indreptat spre directia lui M.
Acest efect este folosit la compasul giroscopic: lasand un giroscop sa se miste liber, de ex. intr-un lagar plutitor, doar intr-un plan orizontal, rotatia Pamantului exercita un moment de rotatie asupra giroscopului, care actioneaza paralel cu suportul vitezei unghiulare a Pamantului. Astfel axa giroscopului se indreapta permanent in directia polului nord geografic (navigatie inertiala).
Momentele cinetice orbitale ale atomilor si momentele cinetice proprii ale nucleelor atomice si ale particulelor elementare, ca urmare a momentelor lor magnetice, capata in camp magnetic momente de rotatie care duc, ca si in cazul giroscopului, la miscari de precesie:
rezonanta electronica de spin;
rezonanta nucleara.