Flotabilitatea navei

Flotabilitatea navei

Flotabilitatea este proprietatea navei de a pluti la suprafata apei sau de a se mentine in imersiune la o anumita adancime impusa.

Flotabilitatea studiaza plutirea libera a navei.

Plutirea libera exclude actiunea momentelor exterioare de inclinare.

Pentru studiul teoretic al flotabilitatii se defineste urmatorul sistem de axe de coordonate:

originea sistemului de axe de coordonate ¤;

axa longitudinala 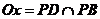, cu sensul pozitiv spre prova;

axa transversala ¤, cu sensul pozitiv spre bordul Tb;

axa verticala ¤, cu sensul pozitiv de la PB in sus.

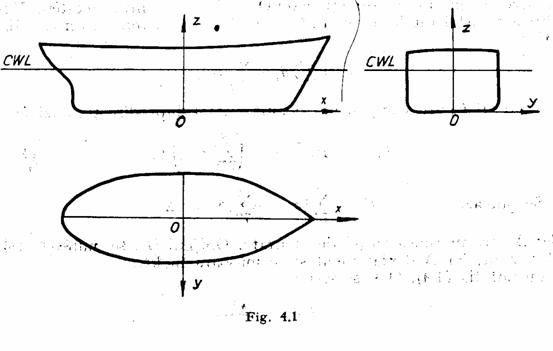
1.1.  Fortele ce actioneaza asupra navei aflata in pozitie de repaus si conditiile de echilibru corespunzatoare acestei pozitii

Asupra navei aflata in pozitie de repaus actioneaza doua categorii de forte: de greutate si de presiune.

Fortele de greutate.

Fortele de greutate se datoreaza actiunii campului gravitational asupra navei.

Forta de greutate are punctul de aplicatie in G, denumit centru de greutate.

Centrul de greutate este definit de punctul de aplicatie al rezultantei fortelor de greutate corespunzatoare maselor elementare din componenta masei navei.

Centrul de greutate G are coordonatele:

abscisa a centrului de greutate definita de distanta de la G la planul yOx;

ordonata a centrului de greutate definita de distanta de la G la planul xOz. Pentru a se asigura o plutire dreapta in plan transversal, inca din faza de constructie, se impune o distributie a greutatilor la bord astfel incat .

Fortele de presiune.

Fortele de presiune se datoreaza presiunii hidrostatice exercitate de apa pe suprafata udata a corpului navei.

Centrul de aplicatie al fortei de presiune este in centrul de carena B.

Centrul de carena B este centrul geometric al volumului carenei navei.

Pozitia centrului de carena este definita de coordonatele:

abscisa a centrului de carena definita de distanta de la B la planul yOz;

ordonata a centrului de carena definita de distanta de la B la planul xOz. In cazul plutirii drepte in plan transversal, volumul carenei este simetric fata de planul xOz si B se afla chiar in acest plan, deci .

Se noteaza cu K proiectia lui B pe PB si se numeste punct de chila.

Echilibrul static presupune ca suma fortelor care actioneaza asupra navei sa fie nula, adica , care este prima conditie de echilibru static a navei si care impune ca marimea fortei de greutate sa fie egala cu marimea fortei de presiune sau, altfel spus, deplasamentul sa fie egal cu impingerea Arhimede.

Echilibrul static impune ca suma momentelor fortelor ce actioneaza asupra navei sa fie nula, adica , care este a doua conditie de echilibru static a navei si care impune ca fortele ce actioneaza asupra ei sa aiba acelasi suport.

Aceste doua relatii reprezinta ecuatiile de echilibru corespunzatoare plutirii drepte a navei.

1.2.  Tipuri de plutiri, parametrii si ecuatiile de echilibru corespunzatoare acestor plutiri

Prin plutire se intelege mentinerea navei intr-o anumita pozitie in raport cu suprafata libera a apei.

Cazul general de plutire a navei corespunde inclinarii atat in plan transversal cat si in plan longitudinal.

Fie si unghiurile de inclinare in plan transversal si longitudinal ale plutirii.

Unghiul de inclinare transversala sau unghiul de banda este unghiul facut de o plutire inclinata in plan transversal cu PB si se considera pozitiv cand nava se inclina spre bordul Tb.

Unghiul de inclinare longitudinala sau unghiul de asieta este unghiul facut de o plutire inclinata in planul longitudinal cu PB si se considera pozitiv cand nava se inclina spre prova.

Inclinarea navei spre prova se numeste aprovare, iar cea spre pupa apupare.

Dand anumite valori particulare unghiurilor si se obtin patru tipuri de plutiri.

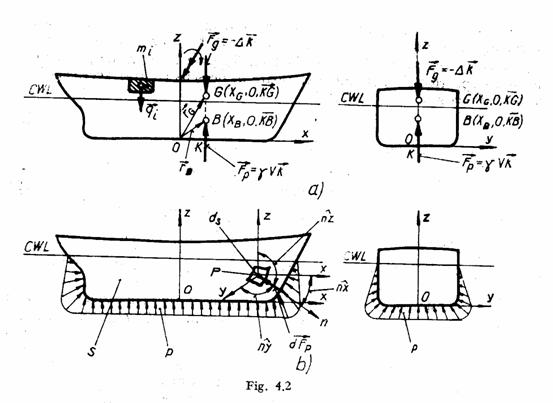
Plutirea dreapta ()

Plutirea dreapta WL este plutirea al carei plan este normal pe PD si paralel cu PB.

Pozitia acestei plutiri fata de PB este definita printr-un singur parametru:

T_¤

Ecuatii de echilibru corespunzatoare plutirii drepte: .

Plutirea inclinata in plan transversal ()

Plutirea inclinata in plan transversal este plutirea al carei plan este normal pe ¤ dar nu este paralel cu PB.

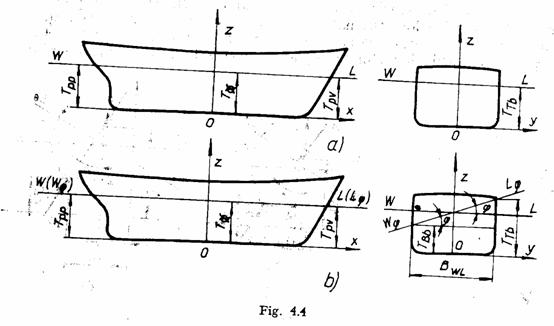
Pozitia acesteia in raport cu PB este definita de urmatorii parametri:

T_¤

Ecuatiile de echilibru sunt:

.

Plutirea inclinata in plan longitudinal ()

Plutirea inclinata in plan longitudinal este plutirea al carei plan este normal pe PD dar nu este paralel cu PB.

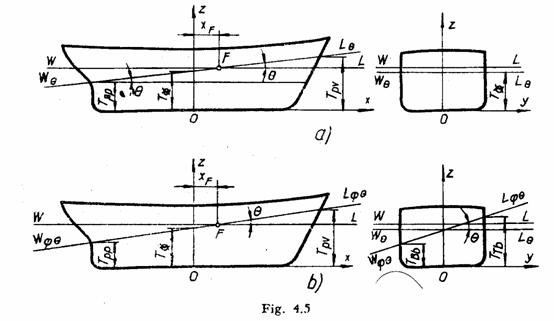
Plutirea se intersecteaza cu WL dupa o axa transversala ce trece prin centrul geometric al plutirii WL.

Pozitia plutirii in raport cu PB este determinata de parametrii:

T_¤

.

Ecuatiile de echilibru sunt:

.

Plutirea inclinata in ambele planuri ()

Plutirea inclinata in plan transversal si longitudinal este plutirea al carei plan nu este paralel cu PB.

Pozitia acestei plutiri in raport cu PB este definita de urmatorii parametri:

T_¤

.

Ecuatiile de echilibru sunt:

.

1.3.  Calculul marimii fortei de greutate si coordonatelor centrului de greutate. Deplasament. Deplasament deadweight. Tonaj.

Calculul marimii fortei de greutate. Deplasament. Deplasament deadweight. Tonaj.

Forta de greutate a navei , unde este o masa elementara, iar este forta de greutate elementara dispusa dupa directia axei Oz.

Marimea greutatii totale a unei nave poarta denumirea de deplasament.

.

Deplasamentul navei goale , in care:

- greutatea corpului etans;

- greutatea suprastructurilor si rufurilor;

- greutatea masinilor principale si instalatiilor aferente;

- greutatea amenajarilor si instalatiilor auxiliare de bord.

Deplasamentul deadweight

- greutatea incarcaturii utile sau a marfii transportate;

- greutatea rezervelor de combustibil, ulei si apa tehnica, necesare functionarii masinilor principale si auxiliare de la bord pentru raza de autonomie a navei;

- greutatea rezervelor de alimente, apa potabila, necesare echipajului, precum si a rezervelor de materiale de intretinere si piese de schimb;

- greutatea echipajului ambarcat la bord si a pasagerilor daca e cazul.

Deplasamentul deadweight este definit de marimea tuturor greutatilor variabile si consumabile, inclusiv a echipajului si pasagerilor, corespunzatoare navei la plina incarcare.

Tonajul brut TB este o marime calculata conventional, care reflecta volumul total inchis de corpul navei inclusiv suprastructurile.

Tonajul net TN este o fractiune din tonajul brut care reflecta capacitatea economica a navei, calculata conventional in functie de volumul spatiului de incarcare si de numarul de pasageri.

Unitatea de masura pentru tonaj este tona registru TR cu cele doua denumiri specifice: tona registru brut TRB si tona registru net TRN.

O tona registru reprezinta volumul a 100 de picioare cubice engleze sau 2,831 m³.

Calculul coordonatelor centrului de greutate

Punctul de aplicatie al fortei de greutate este centrul de greutate .

Se considera nava reprezentata in PD si ¤ si punctul G in care este aplicata forta de greutate a navei de marime Δ. Fie de asemenea o masa elementara cu centrul in punctul asupra careia actioneaza forta elementara de greutate de marime .

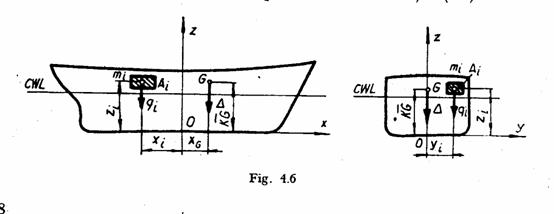
Momentul static al marimii fortei de greutate elementare fata de planul yOz este:

.

Coordonatele sunt:

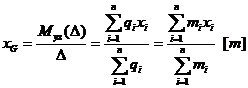
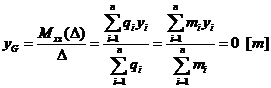
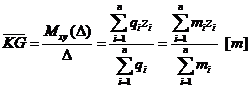
Acest mod de calcul presupune cunoasterea valorilor maselor elementare ce compun masa totala a navei, precum si a pozitie centrelor acestora in raport cu sistemul de axe de coordonate Oxyz.

1.4.  Calculul analitic de carene drepte

Calculul analitic de carene drepte consta in stabilirea relatiilor analitice de calcul pentru trei categorii de elemente.

a.     Elementele geometrice care definesc suprafata plutirii drepte. Din aceasta categorie fac parte:

aria a suprafetei plutirii drepte;

coordonatele ale centrului geometric F al suprafetei plutirii drepte;

momentele de inertie ale suprafetei plutirii drepte fata de axele centrale (longitudinala si transversala) de inertie.

b.     Elementele geometrice care definesc suprafata cuplei teoretice. Din aceasta categorie fac parte:

ariile ale suprafetei jumatatii de cupla si intregii cuple teoretice;

momentele statice ale suprafetei jumatatii cuplei teoretice fata de axele Oz si Oy.

c.      Elementele care definesc carena dreapta. Din aceasta categorie fac parte:

volumul carenei V;

coordonatele ale centrului de carena B.

Calculul ariei suprafetei plutirii drepte

Se considera suprafata de arie definita de conturul navei in planul unei plutiri drepte. Fie aria unui dreptunghi elementar de dimensiuni . Atunci:

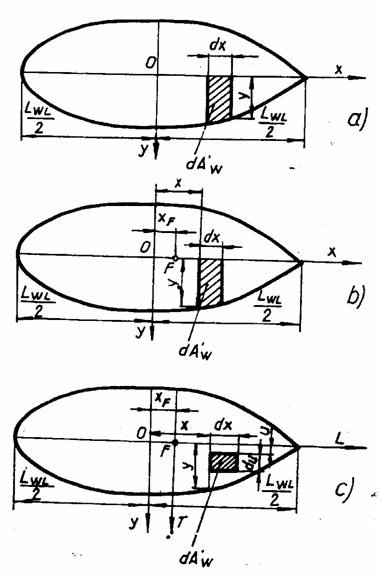
Integrand pe intervalul se obtine aria pentru jumatate din suprafata plutirii.

,

iar aria intregii suprafete a plutirii drepte este:

,

unde .

Calculul coordonatelor centrului geometric al suprafetei plutirii drepte

Se considera suprafata de arie definita de conturul navei in planul unei plutiri drepte, raportata la sistemul de axe de coordonate xOy. Pozitia centrului geometric F al suprafetei plutirii drepte este definita de coordonatele si .

Fie aria unui dreptunghi elementar de dimensiuni , situat la distanta fata de axa Oy ( fiind infinit de mic s-a considerat distanta de la centrul geometric al dreptunghiului elementar pana la axa Oy, ). Momentul static al suprafetei de arie fata de axa Oy este:

.

Integrand pe intervalul si inmultind relatia obtinuta cu 2 se obtine momentul static al suprafetei de arie fata de axa Oy:

,

in care:

Conform definitiei,

.

.

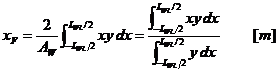Calculul momentelor de inertie ale suprafetei plutirii drepte fata de axele centrale (longitudinala si transversala) de inertie

Se considera suprafata de arie , definita de conturul navei in planul unei plutiri drepte. Fie aria dreptunghiului elementar de dimensiuni situat la distanta x fata de axa Oy si la distanta u fata de axa Ox. Axa centrala longitudinala de inertie L trece prin centrul geometric F al suprafetei plutirii si se suprapune cu Ox. Momentul de inertie al suprafetei de arie fata de L este:

.

Integrand dupa Ox pe intervalul si dupa Oy pe intervalul , se obtine momentul de inertie pentru jumatate din suprafata plutirii drepte fata de L:

,

iar momentul de inertie pentru intreaga suprafata a plutirii drepte este:

,

in care: .

Fie acum momentul de inertie al suprafetei de arie fata de axa Oy:

.

Integrand dupa Ox pe intervalul si dupa Oy pe intervalul , se obtine momentul de inertie pentru jumatate din suprafata plutirii fata de axa Oy:

,

iar momentul de inertie pentru intreaga suprafata a plutirii drepte este:

unde: .

Axa centrala transversala de inertie T, trece prin F si este paralela cu Oy. Se aplica teorema lui Steiner si se obtine relatia analitica de calcul a momentului de inertie al suprafetei plutirii drepte fata de axa T:

.

Calculul volumului carenei

Pentru nava reprezentata in PD se considera ca aria suprafetei definite de conturul navei in acest plan si plutirea dreapta WL este volumul carenei V. Relatia analitica de calcul a volumului carenei se poate stabili in doua moduri: prin integrare pe lungime si prin integrare pe inaltime.

Fie volumul prismei elementare definite de si situata la distanta x fata de planul yOz. Atunci:

,

in care: este aria imersa a sectiunii transversale situate la distanta x fata de planul yOz.

Integrand pe intervalul se obtine:

,

in care: .

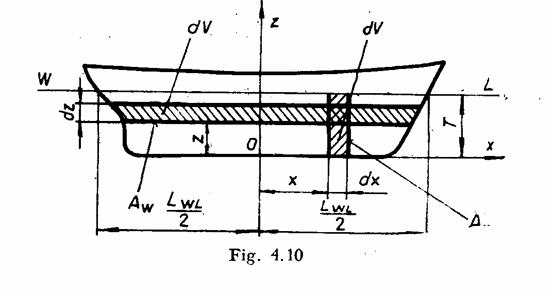
Fie acum volumul prismei elementare definite de si situate la distanta z fata de planul xOz. Atunci:

.

Integrand pe intervalul se obtine:

,

in care: .

In concluzie se poate scrie:

,

unde: .

Calculul coordonatelor centrului de carena

Pozitia centrului de carena B este definita de coordonatele: .

Fie volumul al prismei elementare situate la distanta x fata de planul yOz. Momentul static al lui fata de yOz este:

Integrand pe intervalul se obtine:

.

Conform definitiei:

.

Din cele doua relatii de mai sus, rezulta:

,

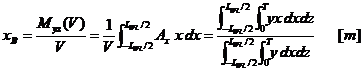in care: .

Fie acum volumul al prismei elementare situate la distanta z fata de planul xOy. Momentul static al lui fata de xOy este:

.

Integrand pe intervalul se obtine:

.

Conform definitiei:

.

Din cele doua relatii de mai sus, rezulta:

,

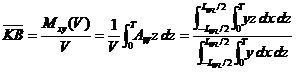in care: .

v    Calculul practic de carene drepte

Geometria complexa a corpului navei nu permite determinarea valorilor exacte ale integralelor si din acest motiv se recurge la utilizarea unor metode aproximative de integrare asa cum este metoda trapezelor.

Calculul ariilor suprafetelor plutirilor drepte, ariilor suprafetelor cuplelor teoretice si volumului carenei corespunzatoare CWL

Graficul functiei prezinta urmatoarelor trei proprietati:

aria suprafetei aflate sub graficul functiei reprezinta la scara ;

abscisa a centrului geometric al suprafetei aflate sub graficul functiei este egala cu abscisa a centrului de carena;

coeficientul de finete al suprafetei aflate sub graficul functiei este egal cu coeficientul de finete longitudinal prismatic al carenei.

Graficul functiei prezinta trei proprietati:

aria A a suprafetei definite de graficul functiei , axa Oz si CWL reprezinta la scara ;

cota centrului geometric al suprafetei definite de graficul functiei , axa Oz si CWL este egala cu cota a centrului de carena;

Coeficientul de finete al suprafetei definite de graficul functiei , axa Oz si CWL este egal cu coeficientul de finete vertical prismatic al carenei.

Calculul volumului carenei si deplasamentului navei corespunzator plutirii drepte

Graficul functiei are doua proprietati:

graficul acestei functii admite axa Oz ca tangenta in origine, deoarece originea este un punct de extrem;

daca prin punctul se duce o dreapta orizontala care intersecteaza Oz in E si tangenta la graficul functiei care intersecteaza Oz in F, atunci valoarea raportului este egala cu coeficientul de finete vertical prismatic pentru pescajul corespunzator lui A.

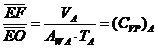
Calculul abscisei centrului plutirii si abscisei centrului de carena

Graficele functiilor au urmatoarea proprietate:

punctele de intersectie ale graficelor functiilor sunt puncte de extrem (minim sau maxim) pentru functia .

Calculul cotei centrului de carena

Graficul functiei prezinta urmatoarea proprietate:

graficul functiei admite axa Oz ca tangenta in origine.

Calculul momentelor de inertie ale suprafetei plutirii drepte fata de axele centrale (longitudinala si transversala) de inertie

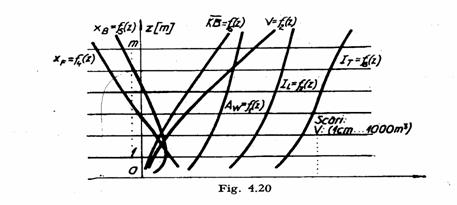
Graficele functiilor se traseaza folosind doua tabele.

Desenul care include graficele functiilor ce au pe z ca variabila independenta se numeste diagrama de carene drepte.

v    Calculul de carene inclinate

Deseori, pozitia navei in raport cu suprafata libera a apei este definita de o plutire oarecare (inclinata atat in plan longitudinal cat si in plan transversal). Pentru studiul conditiilor de echilibru in astfel de situatii este necesar sa se calculeze volumul carenei si coordonatele centrului de carena.

Se considera o nava inclinata in plan longitudinal si transversal cu unghiul θ, respectiv φ, reprezentata prin sectiunea sa in PD si in plan transversal situat la distanta x fata de ¤. Pentru plutirea rezulta volumul carenei si coordonatele ale centrului de carena.

Fie volumul prismei elementare definita de , , situata la distanta x fata de planul ¤. Atunci: .

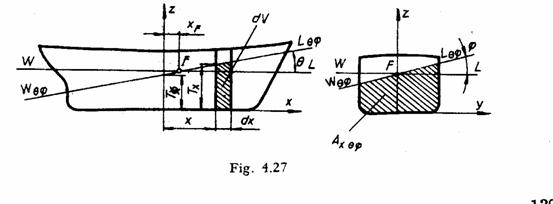
Integrand pe intervalul , se obtine: , unde este aria sectiunii transversale imerse, situate la distanta x fata de planul yOz.

Pentru calculul coordonatelor centrului de carena este necesar in prealabil sa se determine momentele statice ale volumului carenei fata de planurile: .

;

;

,

in care sunt momentele statice ale suprafetei transversale imerse de arie , fata de axele .

Calculul de carene inclinate prin metoda trapezelor

Pentru determinarea , se considera sectiunea transversala situata la distanta x fata de planul yOz, avand trasate pe ea graficele functiilor: .

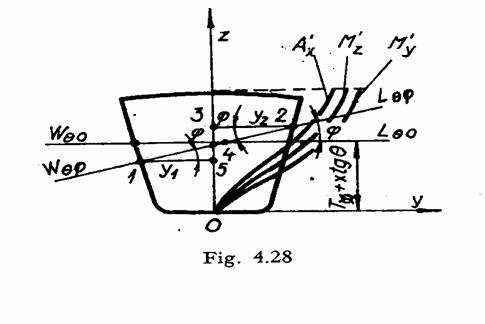
Fie proiectia pe planul sectiunii transversale a plutirii inclinate in plan longitudinal cu unghiul θ. Ea este definita de parametrul:

_¤.

Se obtine:

;

;

_¤,

unde:

- momentul static al suprafetei de ariei , fata de axa Oz;

- momentul static al suprafetei de arie , fata de axa Oz;

1.5.  Ambarcarea (debarcarea) de greutati

Operatiunile de ambarcare (debarcare) de greutati sunt intalnite in mod frecvent in practica exploatarii navelor.

Ambarcarea (debarcarea) de greutati mici

Greutatea mica este considerata acea greutate care ambarcata la bord produce o modificare de pescaj astfel incat bordurile pot fi considerate verticale pe toata lungimea navei.

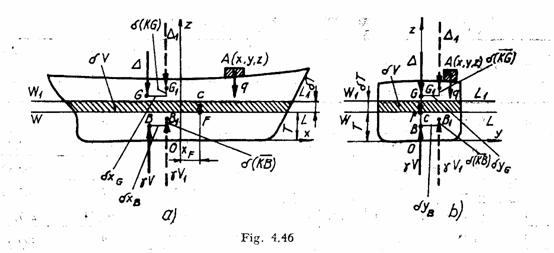
Se considera o nava reprezentata prin sectiunile sale in PD si ¤. Pozitia initiala a navei este definita de plutirea dreapta WL careia ii corespund:

deplasamentul Δ aplicat in centrul de greutate ;

impingerea Arhimedica aplicata in centrul de carena .

Ecuatiile de echilibru static corespunzatoare pozitiei initiale a navei sunt:

;

.

Fie q marimea greutatii care se ambarca in punctul de pe nava. Ambarcarea lui q determina:

modificarea pescajului mediu;

modificarea pozitiei centrului de carena;

modificarea pozitiei centrului de greutate.

Modificarea pescajului mediu

In urma ambarcarii greutatii de marime q, deplasamentul navei creste astfel:

.

Acestui deplasament i se opune impingerea arhimedica:

.

Conform primei conditii de echilibru, avem:

sau

Astfel:

,

in care: este volumul de apa suplimentar dezlocuit de nava ca urmare a ambarcarii lui q si se calculeaza cu relatia:

,

unde: este aria suprafetei plutirii drepte initiale, iar este modificarea pescajului mediu.

Marimii q i se asociaza semnul + la ambarcare, respectiv semnul - la debarcare.

Modificarea pozitiei centrului de carena

In urma ambarcarii greutatilor se modifica volumul carenei, motiv care determina deplasarea centrului de carena din punctul initial in punctul . Deplasarea centrului de carena rezulta din deplasarile elementare . Cauza aparitiei acestor deplasari este volumul suplimentar cu centrul geometric .

Se calculeaza momentele statice ale volumelor si fata de planul transversal ce trece prin B si se egaleaza:

.

In mod analog se determina deplasarile si respectiv coordonatele :

;

.

.

Modificarea pozitiei centrului de greutate

In urma ambarcarii greutatii de marime q, considerata concentrata in punctul , centrul de greutate al navei se deplaseaza din in . Deplasarea centrului de greutate rezulta din deplasarile elementare . Aceste deplasari elementare se determina egaland momentele statice ale marimii greutatii ambarcate fata de cele trei planuri (transversal, longitudinal si orizontal) ce trec prin G, cu momentele statice ale noului deplasament aplicat in fata de aceleasi planuri.

Astfel, pentru determinarea lui se scrie

.

Analog se determina , respectiv :

.

Pentru ca plutirea rezultata in urma operatiunii de ambarcare (debarcare) sa fie dreapta este necesar sa se respecte a doua conditie de echilibru static care presupune:

.

Astfel ca avem:

.

La ambarcarea (debarcarea) greutatii de marime q, inclinarile longitudinale si transversale pot fi evitate daca punctul de ambarcare (debarcare) este dispus pe o verticala ce trece prin centrul plutirii initiale.

Ambarcarea (debarcarea) de greutati mari

Greutatea mare este considerata acea greutate care ambarcata la bord produce o modificare de pescaj astfel incat bordurile nu pot fi considerate verticale pe toata lungimea navei.

Modificarea pescajului mediu si pozitiei centrului de carena in cazul ambarcarii (debarcarii) greutatilor mari se determina cu ajutorul diagramei de carene drepte. In acest scop se utilizeaza graficele functiilor: si se procedeaza astfel:

tinand cont de scara graficului functiei , se masoara, pe axa absciselor, segmentul care materializeaza deplasamentul initial Δ, iar prin punctul rezultat din intersectia verticalei duse la capatul acestui segment cu graficul functiei, se traseaza o dreapta orizontala ce defineste pe axa Oz pescajul initial T;

segmentele masurate pe dreapta orizontala definita mai inainte, intre axa Oz si graficul functiei respectiv , definesc la scarile celor doua functii coordonatele initiale ale centrului de carena;

dupa ambarcarea greutatii de marime q, deplasamentul navei devine: ;

se masoara pe axa absciselor, la scara graficului functiei , segmentul ce materializeaza deplasamentul , caruia ii corespund: ;

variatia pescajului mediu si deplasarile centrului de carena sunt:

.

1.6.  Influenta greutatii specifice a apei asupra pescajului

Greutatea specifica a apei depinde de continutul de saruri si de temperatura, deci ea variaza de la o zona de navigatie la alta.

Trecerea navei dintr-o zona de navigatie in alta, insotita de schimbarea greutatii specifice a apei, duce la modificarea pescajului. In continuare se determina variatia pescajului navei ca urmare a trecerii dintr-o apa cu greutate specifica , intr-o apa cu greutate specifica .

Intrucat pe timpul trecerii deplasamentul navei nu se modifica, rezulta:

.

Conform primei conditii de echilibru se scrie:

.

Astfel, avem:

.

Daca , atunci si avem: .

.

unde este coeficientul de finete vertical prismatic corespunzator situatiei initiale.

La trecerea navei intr-o apa cu greutate specifica mai mica variatia pescajului este pozitiva, iar pescajul creste.

La trecerea navei intr-o apa cu greutate specifica mai mare variatia pescajului este negativa, iar pescajul scade.

1.7.  Rezerva de flotabilitate. Marca de bord liber. Scari de pescaje.

Rezerva de flotabilitate este definita de volumul corpului etans situat deasupra plutirii de plina incarcare. Ea depinde de inaltimea bordului liber.

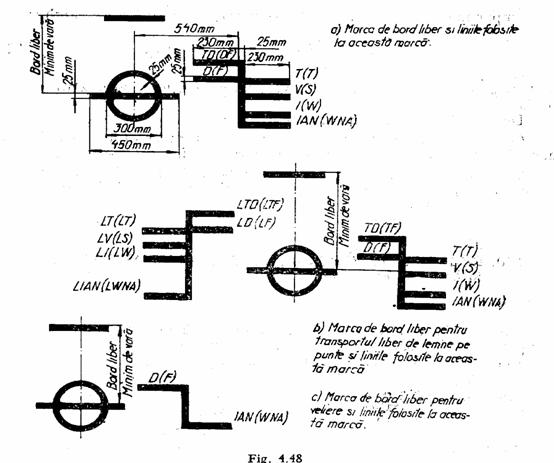
Marca de bord liber este un inel de 25 mm grosime si 300 mm diametru exterior taiat de o banda orizontala de 25 mm latime si 450 mm lungime, a carei margine superioara trece prin centrul inelului. Centrul inelului trebuie sa fie situat la jumatatea lungimii de calcul la o distanta pe verticala de la marginea superioara a liniei puntii egala cu bordul liber minim de vara.

Marca de bord liber este insotita de scara liniilor de incarcare.

Scara liniilor de incarcare este definita de liniile orizontale avand 25 mm latime si 230 mm lungime, care reglementeaza bordul liber pentru principalele zone de navigatie.

Notatiile inscrise in dreptul liniilor ce definesc scara de incarcare au urmatoarele semnificatii:

V (S) este linia de incarcare de vara (summer freeboard) si corespunde benzii care taie inelul marcii;

I (W) este linia de incarcare de iarna (winter freeboard);

IAN (WNA) este linia de incarcare de iarna in Atlanticul de Nord (winter North Atlantic freeboard);

T (T) este linia de incarcare tropicala (tropical freeboard);

D (F) este linia de incarcare de vara in apa dulce (fresh water freeboard);

TD (TF) este linia de incarcare tropicala in apa dulce (tropical fresh water freeboard).

La navele care transporta lemn pe punte, scara liniilor de incarcare obisnuita este dublata de o scara a liniilor de incarcare pentru lemn, dispusa in partea stanga a marcii de bord liber.

Inelul, liniile si literele trebuie sa fie de culoare alba sau galbena daca se aplica pe fond inchis si neagra pe fond deschis.

Scarile de pescaj sunt gradatiile aplicate pe bordaj la prova si pupa navei care permit citirea pescajului la extremitati.

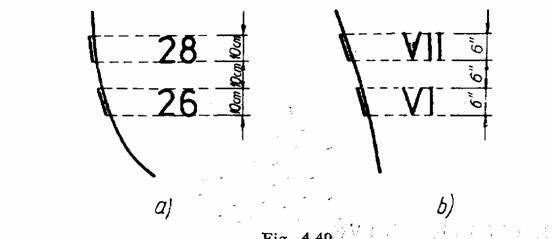
Se intalnesc doua sisteme de marcare a scarilor de pescaje:

sistemul international care prevede marcarea pescajului din 2 in 2 dm, cu cifre arabe avand inaltimea de 1 dm;

sistemul englez care prevede marcarea pescajului in picioare engleze, cu cifre romane avand inaltimea de 6 toli, adica de o jumatate de picior.