
|
|
|
ECOLOGIA POPULATIILOR
Statistica utilizata in ecologia populatiilor
Media este cea mai utilizata variabila statistica. Aceasta, datorita atat simplitatii de calcul cat si datorita modului intuitiv in care este explicata si perceputa.
Media reprezinta suma tuturor valorilor dintr-o serie, impartita la numarul acestor valori.
Iata un exemplu:
Intr-o haita de lupi sunt masurate masele indivizilor respectivi:
Lupul alfa cantareste 13 kg
Lupoaica beta cantareste 11 kg
Patru membri maturi ai haitei cantaresc fiecare cate 8 kg
Doi pui din primavara anului masuratorii cantaresc fiecare cate 3 kg.
Un pui cantareste 2 kg.
Total 9 indivizi
Media indivizilor este de: 13 kg + 11 kg + 4 x 8 kg + 2x 3 kg + 1 x 1kg = 63 kg /9 indivizi = 7 kg/individ.
Dar media respectiva poate insela usor: din cei 9 indivizi studiati, numai 3 sunt sub media respectiva!
Cum aflam atunci cat cantareste un individ mediu din specia Canis lupus?
Raspunsul este: folosind mediana.
Ori de cate ori vom dori sa stim "cat cantareste un individ mediu" sau "care este lungimea chelicerelor la un individ mediu", nu vom utiliza media, ci vom cauta un instrument statistic ce sa ne spuna ceva despre un individ situat "la mijloc"
Aranjand indivizii in ordinea descrescatoare a masei, situatia haitei noastre de Canis lupus arata in felul urmator:
|
Nr. individului |
Masa (kg) |
|
1 |
13 |
|
2 |
11 |
|
3 |
8 |
|
4 |
8 |
|
5 |
8 (mediana) |
|
6 |
8 |
|
7 |
3 |
|
8 |
3 |
|
9 |
1 |
Asta inseamna ca haita are acum 9 indivizi. Individul aflat la mijlocul listei ordonate descrescator (adica, individul numarul 5) are 8 kg. Aceasta este valoarea medianei.
Comparand media cu mediana pentru un set de date, putem sa ne facem o idee despre cat de imprastiate sunt acele date. Cu cat difera mai mult media de mediana, cu atat acele date sunt mai inegal raspindite.
Sa reluam exemplul haitei noastre. In vara, puiul cel mai mic- cel de 1 kg, dispare fiind bolnav iar haitei i se ataseaza un adult de 24 kg, provenit dintr-o haita ce a profitat de un vanat abundent in acel sezon.
Iata cum arata acum structura haitei noastre:
|
Nr. individului |
Masa (kg) |
|
+ 1 |
24 (lupul atasat haitei) |
|
2 |
13 |
|
3 |
11 |
|
4 |
8 |
|
5 |
8 (mediana) |
|
6 |
8 |
|
7 |
8 |
|
8 |
3 |
|
9 |
3 |
|
- 9 |
1 (cel mai tanar membru al haitei a fost rapus de o boala) |
Media= 9 kg/individ. Mediana = 8 (aceeasi cu cea de dinaintea evenimentelor).
Daca am utiliza media pentru a ilustra masa medie a unui individ, am ajunge la concluzia ca masa respectiva se apropie de 9 kg.
Stim insa foarte bine ca exemplarul atasata haitei a carui masa foarte mare a condus la modificarea cu un kg a mediei reprezinta o exceptie - un incident in viata haitei repective si chiar o exceptie pentru specia de Canis lupus.
In acelasi timp, mediana = 8 kg este mult mai aproape de ceea ce stim din descriere despre caracteristicile haitei in cauza, si anume ca un individ mediu are, de regula, 8 kg, rar apropiindu-se de 10-11 kg, nicidecum de cele 19 ale noului individ atasat.
Un indicator statistic precis al imprastierii valorilor intr-un set este abaterea standard despre care vom vorbi mai tarziu.
Acum, schimbarea situatiei haitei, reflectata in medie si - evident - in schimbarea diferentei dintre medie si mediana, duce la o intrebare naturala: cum putem avea o idee cantitativa despre aceasta schimbare, judecand comparativ sitautia de plecare si cea creata prin disparitia puiului si atasarea noului individ?
Prin exprimarea procentuala, in primul rand.
Haita studiata a consumat o biomasa de mamifere mici, in cursul anului de studiu, egala cu 900 kg/an.
Haita din care a provenit individul atasat a consumt tot atat- 900 kg/an.
E acelasi lucru? Asa s-ar parea. Dar sa vedeam cum a fost anul trecut (inaintea anului de studiu):
Haita studiata a consumat 450 kg/an, in timp ce haita de provenienta a noului individ- 675 kg/an.
In ordine, sunt diferite. Dar cat de diferite? Raspunsul este in exprimarea procentuala a abundentei hranei intre cei doi ani:
a) pentru haita studiata: (900-450)/450= 450/450= 100%
b) pentru haita de origine a noului individ: (900-675)/675 = 225/675= 33%
Deducem de aici ca haitei studiate i-a mers mult mai bine - hrana ei a crescut cu 100%, in timp ce haita de origine a avut o hrana mai abundenta cu numai 33%.
Cu toate acestea, individul atasat, este mai greu si intelegem ca a avut mult mai multa hrana disponibila. Cum rezolvam aceasta contradictie?
Prin exprimarea per capita.
D. EXPRIMAREA PER CAPITA, RATE DE CRESTERE SI COMPARATII
Anul trecut, haita studiata avea 9 indivizi, in timp ce haita noului individ avea 25.
Cata hrana a fost consumata de fiecare individ in parte? Adica, per capita?
a) haita studiata: 450 kg/an / 9 indivizi = 50 kg/an.individ
b) haita de origine a noualui individ: 675 kg/an /11 indivizi = 61 kg/an.individ.
In ordine, acest lucru inseaman ca haita de origine a dus-o mult mai bine din punct de vedere al hranei, exprimat in biomasa consumata per capita.
Cum stau lucrurile in anul de studiu?
Haita de origine a crescut de la 11 la 15 indivizi, in urma abundentei hranei.
a) haita studiata: 900 kg/an / 9indivizi= 100 kg/an.individ
b) haita de origine: 900kg/an / 15 indivizi = 60 kg/an.individ
Vrem insa sa vedem ceea ce au simtit lupii, si anume tendintele abundentei hranei intre cei doi ani, pentru cele doua haite. Cum?
Comparam schimbarile in abundenta hranei per capita, intre cei doi ani. Rezulta urmatoarele:
a) Haita studiata: de la 50 kg/an.individ in anul terecut, hrana per capita a crescut la 100 kg/an.individ= crestere de (100 kg/an.individ - 50 kg/an .individ)/ 50 kg/an.individ = 100%
b) Haita de origine a noului individ: scadere de (60 kg/an.individ - 61 kg/an.individ)/ 61 kg/an.individ = - 1,6%
Acum ne explicam de ce noul individ s-a desprins de haita de origine (hrana sa disponibila a scazut procentual fata de anul trecut) si de ce a fost primit in haita studiata (hrana disponibila a crescut puternic).
Doar o astfel de comparatie intre ratele de crestere/scadere a abundentei hranei per capita ne-a putut da o imagine reala despre cauzele modificarilor numerice in cele doua haite.
Trecerea acelui individ de la o haita la alta a condus, dupa cum am vazut, si la modificari in imprastierea valorilor maselor indivizilor in haita. Cum sa masuram insa aceste imprastieri, sau altfel spus- abateri de la medie, intr-un mod care sa fie inteles de toata lumea? Adica standard.
Statisticienii au construit un astfel de instrument: Abaterea Standard.
Datele dintr-un set prezinta o imprastiere determinata fata de medie. Altfel spus, numarul de indivizi cu o anume valaore a masei este cu atat mai mic cu cat ne indepartam de valoarea medie.
Aceasta este o situatie comuna, o distributie a datelor numita normala, de forma urmatoare:
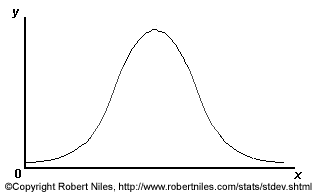
Pe axa x avem caracteristica studiata- de exemplu masa individului din populatia de Canis lupus. Pe y se afla numarul de indivizi caruia ii corespunde o valaore data a masei individuale.
Nu toate distributiile normale arata insa la fel. Cu cat curba este mai strinsa, cu atat valorile caracteristicii sunt mai grupate mai strans in jurul mediei, se abat mai putin de la aceasta. Adica, abbaterea standard este mai mica. Cu cat curba este mai aplatizata, cu atat valorile sunt ma imprstiate. Adica, abaterea standard este mai mare.
Aceasta prezentare intuititiva ascunde un calcul mult mai complicat.
Pentru a intelege insa pe ce bazeaza acel calcul si - de fapt- ce masoara abaterea standard, sa analizam urmataorea figura (exemplu adaptat dupa Robert Niels):
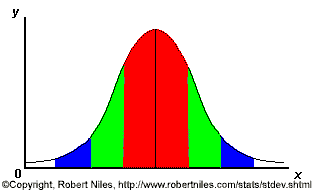
a) In zona rosie, abaterea standard fata de medie acopera 68% din totalul indivizilor.
b) In zona verde, abaterea standard fata de medie acopra 95% din totalul indivizilor
c) In zona albastra, abaterea standard acopera 99% din toalul indivizilor.
Daca am avea de-a face cu o curba mai aplatizata, zona rosie - de exemplu- ar trebui sa fie mult mai lata pentru a putea acoperi 95% din indivizi, adica abaterea standard ar fi mai mare.
De ce e importanta abaterea standard?
Sa luam exemplul celor 2 haite.
In haita studiata, in anul curent, media masei era de 8 kg. In haita din care provenea individul nou, media era de 9 kg. La o prima vedere, am fi tentati sa credem ca haita a doua este alcautuita din indivizi de talie mai mare decat prima.
Dar.
In haita studiata avem 4 indivizi de masa medie, din totalul de 9. In cea de-a doua, doar exemplarul plecat este de talie mare, ceilalti 14 fiind de mase mai mici.
Aceasta insemana ca haita studiata are mai mai multi indivizi apropiati de talia medie decat cea de origine a exemplarului atasat. Statistic, spunem ca respectiva caracteristica este mai grupata in haita studiata decat in celalta, sau ca abatereastandard este mai mare. Grafic, curba distributiei normale la haita studiata este mai aplatizata decat la cealalta.
In ordine, dar cum se calculeaza abaterea standard?
Valorile caracteristicii se aranjeaza intr-un tabel de forma uramtoare:
masa (kg)
Masa medie
(masa- masa medie)
(masa-masa medie)2
13
7
6
36
11
7
4
16
8
7
1
1
8
7
1
1
8
7
1
1
8
7
1
1
3
7
-4
16
3
7
-4
16
1
7
-6
36
Total:
124
Total/n:
13,78
Total/(n-1):
15,50
√(total/n)
3,711842909
√(total/(n-1)
3,937003937
Poate fi o metoda comoda pentru seturi reduse de date, dat in ecologia populatiilor lucram cu seturi mult mai mar ide date: sute- mii- chiar zeci de mii de valori.
In Excel avem:
= STDEV(A1:Z99) ; unde A1:Z99 este setul de date (notatiile pot sa difere usor in functie de versiunea Excel folosita), daca dorim sa folosim metoda prin impartire la "n-1"
si
=STDEVP (A1:Z99); daca dorim sa folosim metoda prin imparitere la "n"
EXEMPLU DE CALCUL
In doua lacuri au fost studiate 2 populatii de trichoptere, seturile de date din probe prezentandu-se dupa cum urmeaza[1]
Anul I de studiu:
Lacul A:
|
Exemplar |
Lungime (mm) |
|
1 |
5 |
|
2 |
4,5 |
|
3 |
4 |
|
4 |
4 |
|
5 |
3,5 |
Lacul B:
|
Exemplar |
Lungime (mm) |
|
1 |
7 |
|
2 |
6 |
|
3 |
4 |
|
4 |
3 |
|
5 |
2,5 |
Anul II de studiu:
Lacul A:
|
Exemplar |
Lungime (mm) |
|
1 |
7 |
|
2 |
5 |
|
3 |
4 |
|
4 |
4 |
|
5 |
3,5 |
Lacul B:
|
Exemplar |
Lungime (mm) |
|
1 |
6 |
|
2 |
5 |
|
3 |
4 |
|
4 |
4 |
|
5 |
2 |
|
6 |
1 |
|
7 |
1 |
Abundenta dusmanilor naturali (pesti) a fost urmatoarea:
|
Numarul de unitati pradatoare echivalente[2] |
Lacul A |
Lacul B |
|
Anul I |
100 |
40 |
|
Anul II |
50 |
80 |
Sa se calculeze media, mediana, schimbarile procentuale in dusmani per capita si abaterile standard si sa se interpreteze ecologic rezultatele.
Rezolvare:
a) media si mediana
|
Lungimea, mm |
Lacul A |
Lacul B |
||
|
Media |
Mediana |
Media |
Mediana |
|
|
Anul I |
4,20 |
4,00 |
4,50 |
4,00 |
|
Anul II |
4,70 |
4,00 |
3,29 |
4,00 |
b) dusmani Per capita
Dusmani/individ
Lacul A
Lacul B
Anul I
20,00
8,00
Anul II
10,00
11,43
c) schimbari procentuale
Dusmani/individ
Lacul A
Lacul B
Anul I -> Anul II
-50,00%
+42,86%
d) abaterea standard
Lacul A, Anul I
Lungmea (mm)
Lungimea medie
Lungimea- Lungimea medie)
Lungimea-Lungimea medie)2
5
4,2
0,8
0,64
4,5
4,2
0,3
0,09
4
4,2
-0,2
0,04
4
4,2
-0,2
0,04
3,5
4,2
-0,7
0,49
Total:
1,30
Total/n:
0,26
Total/(n-1):
0,33
√(total/n)
0,509901951
√(total/(n-1)
0,570087713
Lacul B, Anul I
Lungmea (mm)
Lungimea medie
Lungimea- Lungimea medie)
Lungimea-Lungimea medie)2
7
4,5
2,5
6,25
6
4,5
1,5
2,25
4
4,5
-0,5
0,25
3
4,5
-1,5
2,25
2,5
4,5
-2
4
Total:
15,00
Total/n:
3,00
Total/(n-1):
3,75
√(total/n)
1,732050808
√(total/(n-1)
1,936491673
Lacul A, anul II
Lungmea (mm)
Lungimea medie
Lungimea- Lungimea medie)
Lungimea-Lungimea medie)2
7
4,7
2,3
5,29
5
4,7
0,3
0,09
4
4,7
-0,7
0,49
4
4,7
-0,7
0,49
3,5
4,7
-1,2
1,44
Total:
7,80
Total/n:
1,56
Total/(n-1):
1,95
√(total/n)
1,24900
√(total/(n-1)
1,39642
Lacul B, anul II
Lungmea (mm)
Lungimea medie
Lungimea- Lungimea medie)
Lungimea-Lungimea medie)2
6
3,29
2,71
7,3441
5
3,29
1,71
2,9241
4
3,29
0,71
0,5041
4
3,29
0,71
0,5041
2
3,29
-1,29
1,6641
1
3,29
-2,29
5,2441
1
3,29
-2,29
5,2441
Total:
23,43
Total/n:
4,69
Total/(n-1):
5,86
√(total/n)
2,16466
√(total/(n-1)
2,42016
[1] In studiile populationale reale, nuamrul de indivizi colectati este mult mai mare: de ordinul sutelor si miilor; aici avem un exemplu didactic, pentru usurinta calculelor
[2] Pestii consuma cantitati diferite de trichoptere (larve) in functie de specie si de marimea individului- aici am considerat "o unitate echivalenta" de pradator, penrtu a simplifica exercitiul