|
|
|
Legea conservarii sarcinii electrice
Experienta
arata ca un sistem de corpuri electrizate, daca nu schimba
energie (lucru mecanic, caldura etc.) cu nici un alt sistem si
campul electric pe care il produce nu variaza in timp (adica in orice
punct al acestui sistem 
ceea ce -de fapt-
inseamna ca sistemul se afla in regim electrostatic), suma
sarcinilor electrice ale tuturor corpurilor sistemului considerat este
constanta.
Daca,
global sau local, starea de electrizare a corpurilor variaza in timp
(adica atunci cand 
sau/si 
) sistemul de corpuri capata o stare denumita
electrocinetica, stare pusa in evidenta de efecte cu totul
specifice (care au fost descrise in § 1.2.1, aliniatul "Starea
electrocinetica"). Pentru descrierea cantitativa a starii
electrocinetice a corpurilor s-au introdus -in teoria macroscopica a
campului electromagnetic- marimile: intensitatea curentului electric de
conductie i (global) si,
local, densitatea de curent 
(v. § 1.2.1).
Legea
conservarii sarcinii electrice exprima legatura care exista
intre marimile de stare electrocinetica a corpurilor (i si ) si marimile de stare electrica a corpurilor
(q si 
), lege care se verifica experimental in orice
situatie, fara exceptie, si apare -formal identic-
si in alte teorii ale fenomenelor electromagnetice (cum ar fi cea
relativista si cea cuantica, precum si in teoria electronica).
In fond, legea conservarii sarcinii electrice nu numai ca da o
forma cantitativa unui fapt calitativ (adica faptului ca
variatia in timp a starii electrice a corpurilor duce la o noua
stare calitativa a corpului, cea electrocinetica), ci realizeaza
si o armonizare semantica relativa la marimile de stare a
corpurilor, definind ca orice variatie in timp a sarcinii electrice
din interiorul unei suprafete inchise inseamna existeta unui
curent electric prin acea suprafata si -mai precis- viteza de
variatie in timp a sarcinii electrice inseamna, cantitativ,
intensitatea curentului electric de conductie.
Legea conservarii sarcinii electrice se poate exprima atat printr-un model global (relativ la orice suprafata inchisa dintr-un camp electromagnetic), cat si prin unul local (referitor la orice punct din camp).
Modelul global (integral) al legii conservarii sarcinii electrice
Fie
o suprafata inchisa Σ, oricare dintr-un camp
electromagnetic W, in interiorul careia se
afla o sarcina electrica qS atunci viteza de variatie in timp a acestei sarcini
electrice rezulta din existenta unui curent electric de
conductie prin Σ, a carui intensitate instantanee (adica in
fiecare moment t): 
este egala cu
viteza de scadere a sarcinii electrice 
ceea ce se exprima prin modelul:
(1.90) 
Conform definitiei derivatei, se poate scrie:
(D) 
in care 
adica o
variatie in timpul 
a sarcinii electrice,
ca functie de timp, q(t); daca variatia sarcinii
este 
adica 
inseamna ca
sarcina electrica din interiorul suprafetei Σ creste si atunci curentul electric relativ la
suprafata Σ:
(I) 
,
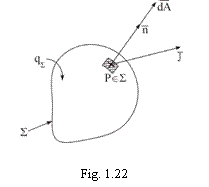are sensul
spre interiorul suprafetei Σ, cu
alte cuvinte (v. fig. 1.22) la sensul de referinta al versorului
normalei locale 
la Σ, totdeauna spre exterior, vectorul
densitatii de curent in 
are sensul spre
interiorul lui 
ceea ce face ca
integrala precedenta (I) sa dea rezultatul 
si derivata (D)
rezulta pozitiva. In caz contrar, daca 
adica
inseamna ca sarcina electrica 
scade, deci derivata (D) are semnul minus, deci curentul electric relativ la Σ dat
de integrala (I) are sensul spre
exteriorul lui Σ, ceea ce inseamna ca in produsul 
este pozitiv, sensul
vectorului densitatii de curent 
fiind de la punctul 
spre exterior (fig.
1.22).
In
acest fel se explica, numai prin utilizarea modelelor si
semnificatiei date de teoria macroscopica (fenomenologica)
marimilor de stare sarcina electrica, intensitatea curentului de
conductie si densitatea de curent, dintre care primele doua sunt
marimi primitive, semnul minus din modelul (1.90) al legii
conservarii sarcinii electrice. (In teoria electronica, intensitatea
curentului electric i este
considerata ca limita raportului dintre suma algebrica a sarcinilor
electrice 
ale particulelor microscopice libere - electroni negative, pozitroni+, ioni si anioni, etc.
- care trec prin sectiuni ale corpului conductor sau prin vid intr-un
interval de timp si durata 
a acestuia, adica
. In acest caz este nevoie de alegerea unui sens de
referinta arbitrar pentru curentul i in functie de sensul de deplasare al particulelor cu
sarcina pozitiva sau cu sarcina negativa, de obicei
alegandu-se sensul de miscare al sarcinilor pozitive, deci invers sensului
de miscare al electronilor. Astfel, daca sensul + al lui i corespunde sensului de trecere prin
suprafata 
a particulelor cu
sarcina +, sensul minus al legii 1.90 rezulta de la sine.)
Dimensional, legea (1.90) arata:
sau 
(1.91)
ceea ce justifica ecuatia dimensionala (1.85).
Introducandu-se
expresia lui 
, din relatia (I), in membrul stang al legii (1.90)
si expresia lui 
in functie de
densitatea de volum a sarcinii electrice
din relatia (1.6), legea conservarii electrice are si forma:
care este tot o forma
globala (integrala) a legii si in care integrala de volum din
membrul din dreapta egalitatii se extinde asupra volumului 
delimitat de
suprafata inchisa S
Modelul local (de punct) al legii conservarii sarcinii electrice
Pentru
determinarea acestui model, se pleaca de la forma integrala 
a legii
conservarii sarcinii electrice in care:
membrul din
stanga referitor la fluxul vectorului prin S se inlocuieste, pe baza formulei (9.20) a lui
Gauss-Ostrogradski (v. § 9.1.2), cu integrala de volum extinsa la 
a divergentei lui
, adica:
(GO)
membrul din dreapta, presupunand -in cazul general-
ca particule prin suprafata S sau chiar S, se deplaseaza in campul electromagnetic cu o
viteza de translatie 
, ceea ce inseamna ca densitatea de volum a
sarcinii electrice este o functie de
timp t si de punct 
adica este 
sau -intr-un sistem de
referinta cartezian atasat corpurilor- este 
se inlocuieste cu
derivata substantiala in raport cu timpul 
a unui camp scalar (v.
§ 9.1.2., relatia 9.48) -numita si derivata integralei de volum
in raport cu timpul-, adica:
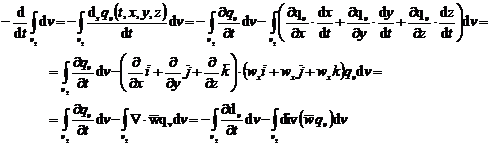(DS)
Egalandu-se,
conform modelului , expresiile din membrul drept al relatiilor (GO)
si (DS) rezulta:
care este o alta
forma a modelului integral (global, relativ la un volum , delimitat de o suprafata inchisa S, oricare din campul W) al legii conservarii sarcinii electrice. Ea pune
in evidenta faptul ca variatia sarcinii electrice locale in
timp este datorata atat curentului de conductie (prin ) cat si celui de convectie local (prin 
).
Deoarece
expresia este valabila
pentru orice volum din domeniul W, se obtine imediat:
(1.92) 
,
care este modelul local al legii conservarii sarcinii electrice, scris adesea si sub forma:
Modelul (1.92) este valabil numai in domeniile de continuitate si netezime (adica fara suprafete de discontinuitate).
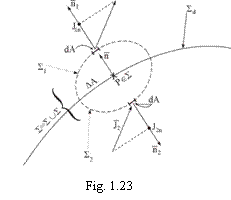
In
cazul suprafetelor de
discontinuitate 
(fig. 1.23), se alege
un punct oarecare 
si o
suprafata elipsoidala (inchisa) S cu centrul in P,
impartita in doua suprafete semielipsoidale 
si 
, de o parte si de alta a suprafetei de
discontinuitate , astfel ca 
(v. fig. 1.23).
In
conditiile din figura 1.23, curentul 
prin mica
suprafata elipsoidala va fi:
(ID) 
,
iar daca suprafata elipsoidala se
restrange la limita spre mica suprafata 
, cu 
, "lipindu-si" suprafetele semielipsoidale de 
, dinspre o parte si alta a suprafetei de
discontinuitate 
(adica 
, cu ), integrala (ID) devine:
(I
) 
si deoarece conform conventiei clasice,
versorii normalei la 
se iau cu sensul spre
exterior: 
, expresia lui din (I
) devine:
(IJ) 
.
La limita, cand 
sarcina electrica
, din interiorul suprafetei S este sarcina aflata chiar pe suprafata , ce devine - daca are densitatea de suprafata
a sarcinii electrice 
:
(Q) 
,
daca este suficient de
mica astfel incat 
= const. in 
.
Atunci, inlocuindu-se in (1.90) membrul din stanga cu
expresia lui data de (IJ) si 
cu expresia lui (Q),
legea conservarii sarcinii electrice ia forma (in conditiile
aratate in figura 1.23):
sau:
(1.93) 
,
care este forma locala a
legii conservarii sarcinii electrice intr-un punct P de pe o suprafata de discontinuitate, punct in care
densitatea de suprafata a sarcinii electrice este 
.
Introducandu-se
notiunea "divergenta de suprafata a unui vector" (aici
a lui 
) prin definitia:
,
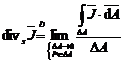astfel ca cei doi membrii ai legii (1.90), in
conditiile suprafetei de discontinuitate din figura 1.23, se
pot scrie in formele:
dA si 
dA.
Atunci legea (1.90) devine:
sau 
dA,
adica:
sau 
(1.93')
cu conditia ca suprafata de discontinuitate sa fie
imobila. Expresia (1.93') reprezinta o alta forma a legii
conservarii sarcinii electrice pe suprafetele de discontinuitate.
In cazul particular al unei suprafete de
discontinuitate fara sarcina electrica 
sau fara
variatia ei in timp (
) si imobila legea (1.93) devine:
sau 
sau 
, (1.94)
ceea ce inseamna ca in acest caz (cu 
), componentele normale 
si 
se conserva prin
suprafetele de discontinuitate neelectrizate sau in regim static.
