Johannes Kepler - Biografie, Demonstratie

Johannes Kepler

1.           Biografie

Astronom, mecanician si matematician german, nascut la Weil der Stadt, Wurttemberg, unul dintre fondatorii astronomiei moderne. Studiile si le-a facut la seminarul teologic protestant din Tubingen. A fost profesor de astronomie si morala la Graz. Intreaga sa activitate l-a definit ca un tenace si abil calculator, un mare vizionar si om de stiinta, dotat cu o bogata imaginatie. Mai toate preocuparile sale stiintifice, teoretice sau de ordin practic, ce sunt legate de domeniul astronomiei, pasiunea lui de o viata, care avea sa-i asigure celebritatea. In 1593 a elaborat lucrarea Prodromus in care a cautat sa determine distantele dintre planete si soare pe baza considerarii corpurilor geometrice perfecte avand convingerea, ca si Pitagora, ca Universul este perfect. Tycho Brahe l-a ales drept colaborator la observatorul din Praga si la moartea acestuia in 1601 va deveni astronom al imparatilor Rudolf II, Mathias II si Ferdinand II intre anii 1601-1630. Utilizand multitudinea de informatii pretioase ramase de la Tycho Brahe ca si din observatiile comune in special asupra planetei Marte, Kepler va anunta in 1609 primele sale doua legi fundamentale privind miscarile planetare in lucrarea ramasa si ea celebra Astronomia nova, al caror continut este urmatorul: L1) Planetele descriu eclipse, Soarele fiind plasat intr-unul din focare. L2) Razele vectoare ale planetelor descriu arii egale in timpuri egale. Dupa detronarea lui Rudolf II in 1612, Kepler primeste din partea noului imparat sarcina de a impune calendarul gregorian, ceea ce il conduce la a intra in conflict atat cu biserica catolica cat si cu cea protestanta. Cu toate neplacerile unui astfel de conflict, deloc de neglijat in general si mai ales pentru acele vremuri, Kepler isi continua cercetarile sale si in 1619, gratie bogatei sale fantezii creatoare, descopera relatia dintre axele mari ale orbitelor planetare si timpul de revolutie al planetelor si publica legea a treia ce ii poarta numele in lucrarea Harmonices mundi libri V la Linz, al carei continut este: L3) Patratele timpurilor de revolutie ale planetelor sunt proportionale cu cuburile semiaxelor mari. Tot in acele vremuri a investigat paralaxa si teoria eclipselor. A alcatuit tabele cu efemeridele planetelor. Dupa izbucnirea razboiului de 30 de ani, este nevoit sa paraseasca Linzul, fiind o vreme, astronom si astrolog al; generalului Wallenstein. In afara cercetarilor de astronomie care i-au adus si bucurii si necazuri, dar i-au asigurat nemurirea in lumea stiintei, Kepler a obtinut alte rezultate valoroase. In anul 1612, an foarte bogat in recoltele de struguri, Kepler, aflat la Linz, s-a interesat de regulile practice de determinare a volumului butoaielor cu vin si in 1615 publuca lucrarea Noua metoda de masurare a butoaielor cu vin. In 1616 va publica o editie populara a acesteia sub titlul Extras din stavechea arta de a masura a lui Arhimede etc. Desi Kepler nu dispunea de o teorie dezvoltata asupra infinitului mic, el a folosit in cartea amintita aceasta notiune in acelasi fel in care, cu un secol mai tarziu, va fii utilizata diferentiala in geometrie. El impartea suprafetele si corpurile in portiuni elementare pe care le suma. Calauzindu-se dupa noua sa idee Kepler a fost primul care a depasit rezultatele obtinute de antici in aceasta directie. A determinat in total marimile a 87 de corpuri noi. In plus cercetarile lui Kepler asupra formei butoaielor ce reda cea mai mare capacitate la cel mai mic consum material, l-au condus spre probleme de maxim si la probleme izoperimetrice, in a caror analiza va urma calea indicata de Pappus in cartea V din Culegerea sa. A stabilit formulele pentru calculul laturilor triunghiului sferic in functie de unghiuri. A studiat poligoanele si poliedrele regulate stelate, publicand rezultatele in 1619. A aratat ca dintre toate paralelipipedele inscrise intr-o sfera, cubul are volumul maxim(1615). A studiat si aplicat in cercetarile sale astronomice concepte ale teoriei conicelor. Astfel a introdus notiunea de excentricitate, a privit asimptotele hiperbolei ca tangente la infinit, a aratat ca parabola este limita unei elipse cand unul dintre focare tinde catre infinit(1609).A avut contributii in optica, mai ales relativ la lunete, construind una in 1611. A studiat lumina, a introdus conceptul de raza de lumina, a explicat reflexia si refractia si a formulat teoria telescoapelor.A elaborat un numar insemnat de lucrari de astronomie, astrologie, matematica precum: Calendarum und Prognosticum, Prodromus dissertationum cosmographicamm continens mysterium ccosmographicum., De fundamentis astrolegiae certioribus, Judicium de trigono igneo, Ad vitellionem paralipomena quibus astronomiae pars optica traditur si multe altele.

2    .demonstratie

In urma observatiilor astronomice J. Kepler a stabilit in anul 1619 legile care descriu miscarea planetelor in jurul Soarelui. Acestea, numite si legile lui Kepler, sunt urmatoarele:

planetele se misca pe elipse ce au Soarele situat intr-unul dintre focare.

raza vectoare a planetei descrie arii egale in intervale de timp egale (legea ariilor).

patratele perioadelor de revolutie sunt direct proportionale cu cuburile semiaxelor mari,adica:

T² = CR³,

unde  prin perioada de revolutie T se intelege timpul in care planeta descrie o elipsa completa.

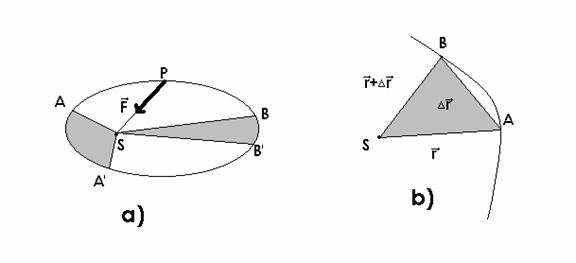
Daca raza vectoare a planetei descrie ariile SAA' si SBB' in intervale egale de timp, conform legii a doua a lui Kepler, aceste arii sunt egale.

In cele ce urmeaza vom trata Soarele si planetele ca pe niste puncte materiale, avand in vedere ca dimensiunile lor sunt neglijabile in comparatie cu distantele ce le separa.

In anul 1687 I. Newton a reusit sa explice legile miscarii planetelor presupunand ca Soarele exercita o forta de atractie asupra planetelor. Aceasta forta de atractie se manifesta ca o forta centripeta ce obliga fiecare planeta in parte sa se miste dupa o curba inchisa, de forma unei elipse. Newton a demonstrat ca daca se admite ca forta de atractie F din partea care actioneaza asupra planetei P este proportionala cu produsul dintre masele acestora si invers proportionala cu patratul distantei r dintre ele, fiind indreptata catre Soare dupa directia PS, atunci pot fi explicate cele trei legi ale lui Kepler. S-a presupus deci ca forta este data de relatia:

unde M_S este masa Soarelui, M_P este masa planetei iar k o constanta de proportionalitate.

Sa cautam, sa demonstram legile lui Kepler. Pentru a scrie pe sub forma vectoriala, sa consideram vectorul indreptat de la S la P si sa avem in vedere ca forta are directia lui , dar sensul contrar acestuia. Prin urmare:

Momentul acestei forte fata de punctul S este:

Folosind ecuatia , rezulta ca momentul cinetic este constant in timp, pastrand aceeasi marime, directie si sens in tot timpul miscarii. Din produsul vectorial se observa ca si , ceea ce inseamna ca vectorii si sunt perpendiculari in tot cursul miscarii pe vectorul constant , adica si , deci si traiectoria, se afla in planul perpendicular pe , plan care trece prin S. Traiectoria miscarii este o curba care se gaseste in acelasi plan.

Determinarea formei geometrice a acestei traiectorii plane necesita calcule mai complicate care arata ca traiectoria este fie o elipsa, fie o parabola, fie o hiperbola, dupa cum viteza initiala a corpului aflat sub actiunea fortei este mai mare sau mai mica.

In cazul planetelor, viteza initiala corespunde conditiilor de miscare pe elipse. In concluzie, forta explica prima lege a lui Kepler.

Sa consideram acum o portiune din traiectorie. Aria a triunghiului hasurat este data de modulul vectorului:

Impartind cu intervale de timp , in care Pamantul s-a deplasat din A in B, obtinem:

si daca presupunem foarte mic (= 0) rezulta:

deoarece pentru foarte mic arcul AB coincide cu coarda (in limita = 0). este tocmai aria suprafetei maturate de raza vectoare in intervalul de timp . Deoarece = const., pentru orice interval de timp putem scrie:

Se vede imediat din ultima relatie ca in unitatea de timp, indiferent de pozitia instantanee a planetei pe traiectorie, raza vectoare a acestuia descrie o suprafata de aceeasi marime, .

Prin urmare, in intervale de timp egale, raza vectoare a planetei descrie arii egale, am obtinut deci si a doua lege a lui Kepler.

Deoarece demonstratia legii a treia a lui Kepler este mai dificila din punct de vedere matematic, vom simplifica lucrurile, presupunand ca traiectoria planetei este circulara (aceasta situatie corespunde satelitilor artificiali care se misca pe orbite circulare). Egaland forta de atractie cu forta centripeta, obtinem:

unde am avut in vedere ca distanta de la planeta la Soare este egala cu raza R a cercului. Rezulta de aici relatiile:

deci

Notand constanta cu c, obtinem a treia lege a lui Kepler:

deoarece, in miscarea circulara, distanta de la un punct oarecare de pe circumferinta pana la centru este egala cu raza cercului. Cercul poate fi considerat ca un caz particular de elipsa cu semiaxele egale intre ele si egale cu raza R a cercului.

Daca tinem seama de dimensiunea Soarelui si planetelor, toata expunerea de mai sus ramane valabila, prin intelegand insa vectorul ce uneste centrul Soarelui cu centrul planetei.

Dupa cum se remarca din relatia F_ext = F₀ cos ω t, directia fortei de atractie trece intotdeauna prin centrul Soarelui. O astfel de forta, a carei directie trece printr-un punct fix se numeste forta centrala.

Pe langa atractia Soarelui, planeta noastra este supusa si atractiei din partea celorlalte planete din sistemul solar. Dintre toate acestea, cea mai importanta este insa forta de atractie a Lunii, care este totusi de 127 de ori mai mica decat atractia solara (mai exact ). Fortele de atractie a Soarelui si a Lunii sunt dirijate respectiv dupa directiile ce unesc centrul Pamantului cu centrul celor doua corpuri ceresti, situate la distantele D si respectiv d (fig. 3).

Forta totala care actioneaza asupra Pamantului este:

deci, in miscarea M de revolutie, Pamantul are acceleratia: