Sintezele lui newton

SINTEZELE LUI NEWTON

Sintezele lui Newton

Kepler propusese trei Legi ale miscarii planetelor bazate pe datele lui Brahe. Se presupunea ca aceste Legi sunt valabile numai in cazul miscarii planetelor; nu se mentiona nimic despre celelalte miscari din Univers. Era clar ca aceste legi erau valabile, dar nimeni nu cunostea o explicatie a acestora.

Newton a schimbat toate acestea.La inceput, el a demostrat ca miscarea obiectelor pe Pamant poate fi descrisa de cele trei noi Legi ale miscarii. Newton a aratat ca cele trei Legi ale miscarii planetelor ale lui Kepler nu erau altceva decat cazuri particulare ale propriilor sale legi (se presupunea ca intre toate corpurile din Univers care poseda masa exista forte de atractie gravitationala). De fapt, Newton a mers chiar mai departe: el a aratat ca Legile miscarilor planetelor ale lui Kepler erau numai aproximativ corecte, si a facut corecturile cantitative care cu observatii detaliate s-au demonstrat a fi valabile.

Atractia universala. Camp gravitational.

In urma observatiilor astronomice, J.Kepler a stabilit in anul 1916 legile care descriu miscarea planetelor in jurul Soarelui. Acestea, numite si legile lui Kepler, sunt urmatoarele:

planetele se misca pe elipse ce au Soarele situat intr-unul dintre focare;

raza vectoare a planetei descrie arii egale in intervale de timp egale.

patratele perioadelor de revolutie sunt direct proportionale cu cuburile semiaxelor mari, adica

T² = CR³

unde prin perioada de revolutie T se intelege timpul in care planeta descrie o elipsa completa.

P B B

Dr A

B' r + Dr

r

A

A' S

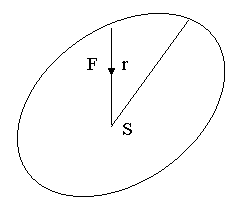
Daca raza vectoare a planetei descrie ariile SAA' si SBB' in intervale egale de timp, conform legii a doua a lui Kepler, aceste arii sunt egale.

In cele ce urmeaza vom trata Soarele si planete ca pe niste puncte materiale, avand in vedere ca dimensiunile lor sunt neglijabile in comparatie cu distantele ce le separa.

In anul 1687 I. Newton a reusit sa explice legile miscarii planetelor presupunand ca Soarele exercita o forta de atractie asupra planetelor.Aceasta forta de atractie se manifesta ca o forta centripeta ce obliga fiecare planeta in parte sa se miste dupa o curba inchisa de forma unei elipse. Newton a demonstrat ca daca se admite ca forta de atractie F din partea Soarelui care actioneaza asupra planetei P este proportionala cu produsul dintre masele acestora si invers proportionala cu patratul distantei r dintre ele, fiind indreptata catre Soare dupa directia PS, atunci pot fi explicate cele trei legi ale lui Kepler. S-a presupus deci ca forta este data de relatia

M_s m_p

F = K

r²

unde M_s este masa Soarelui, m_p este masa planetei iar K este o constanta de elasticitate.

Sa cautam sa demonstram legile lui Kepler .

Pentru a scrie pe F sub forma vectoriala, sa consideram vectorul r indreptat de la S la P si sa avem ca forta are directia lui r , dar sensul contrar al acestuia. Prin urmare

M_s m_p rM_sm_p

F = -K = -K r

r²r r³

Momentul acestei forte fata de punctul S este

M_sm_p

M_F = r X F = -Kr X r = 0

r₃

Folosind ecuatia, DL₀ /Dt = 0, rezulta ca momentul cinetic L = r x p este constant in timp, pastrand aceeasi marime, directie si sens in tot timpul miscarii.

Din produsul vectorial L= r X p se observa ca L r si L p, ceea ce inseamna ca vectorii r si p sunt perpendiculari in tot cursul miscarii pe vectorul constant L, adica r si v, deci si traiectoria, se afla in planul perpendicular pe L, plan care trece prin S. Traiectoria miscarii este o curba care se gaseste in acelasi plan.

Determinarea formei geometrice a acestei traiectorii plane necesita calcule mai complicate care arata ca traiectoria este fie o elipsa, fie o parabola, fie o hiperbola , dupa cum viteza initiala a corpului aflat sub actiunea fortei este mai mare sau mai mica. In cazul planetelor viteza initiala corespunde conditiilor de miscare pe elipse.

In concluzie, forta de atractie explica prima lege a lui Kepler.

Sa consideram acum o portiune din traiectorie. Aria DS a triunghiului ASB

este data de modulul vectorului

1

DS =r X Dr

2

Impartind cu intervalul de timp Dt, in care Pamantul s-a deplasat din A in B, obtinem

si daca presupunem Dt foarte mic (Dt 0), rezulta

Deoarece pentru Dr foarte mic arcul AB coincide cu coarda AB (in limita Dt 0), DS=1/2m_pLDt este tocmai aria suprafetei masurate de raza vectoare in intervalul de timp Dt. Deoarece L=constant, pentru orice interval de timp Dt putem scrie

Se vede imediat din ultima relatie ca in unitatea de timp, indiferent de pozitia instantanee a planetei pe traiectorie, raza vectoare a acesteia descrie o suprafata de aceeasi marime, DS/Dt=L/2m_p

Prin urmare, in intervale de timp egale, raza vectoare a planetei descrie arii egale; am obtinut deci si a doua lege a lui Kepler.

Deoarece demonstratia legii a treia a lui Kepler este mai dificila din punct de vedere matematic, vom simplifica lucrurile, presupunand ca traiectoria planetei este circulara ( aceasta situatie corespunde satelitilor artificiali care se misca pe orbite circulare ). Egaland forta de atractie cu forta centripeta obtinem

M_sm_p

K =m_pw²R

R²

unde am avut in vedere ca distanta de la planete la Soare este egala cu raza R a cercului. Rezulta de aici relatiile:

4p² 4p²

KM_s=w²R³=, deci T²=

T²R³ KM_sR³

Notand costanta 4p²/KM_s cu C, obtinem a treia lege a lui Kepler

T²=CR³,

deoarece, in miscarea circulara, distanta de la un punct oarecare de pe circumferinta pana la centru este egala cu raza cercului. Cercul poate fi considerat ca un caz particular de elipsa cu semiaxele egale intre ele si egale cu raza R a cercului.

Daca tinem seama de dimensiunile Soarelui si planetelor, toata expunerea de mai sus ramane valabila, prin r intelegand insa vectorul ce uneste centrul Soarelui cu centrul planetei.

Dupa cum se remarca , directia fortei de atractie trece intotdeauna prin centrul Soarelui. O astfel de forta, a carei directie trece printr-un punct fix, se numeste forta centrala.

Pe linga atractia Soarelui, planeta noastra este supusa si atractiei din partea celorlalte planete din sistemul solar. Dintre toate acestea, cea mai importanta este insa forta de atractie F_L din partea Lunii, care totusi de 127 de ori mai mica decat atractia solara ,mai exact

Fortele de atractie F_s a Soarelui si F_L a Lunii sunt dirijate respectiv dupa directiile ce unesc centrul Pamantului cu centrele celor doua corpuri ceresti, situate la distantele D si, respectiv, d.

Forta totala care actioneaza asupra pamantului este

M_S m_p m₁ m_p

F = F_s + F_L =K D+K d

D³d³

deci, in miscarea sa de revolutie, Pamantul are acceleratia

Conform principiului al treilea al mecanicii, Pamantul actioneaza asupra Soarelui cu o forta (-Fs ) si asupra Lunii cu o forta (-F_L ) .Aceste forte care au punctele de aplicatie in centrul Soarelui, si, respectiv in centrul Lunii, se comporta ca niste forte centrifuge.

Newton a generalizat relatiile, considerand ca intre orice pereche de corpuri din univers se manifesta o forta de atractie de forma

unde m₁ si m₂ sunt masele celor doua corpuri, iar r₁₂ este distanta ce separa centrele lor. Constanta K se numeste constanta atractiei universale, fiind aceeasi pentru toate perechiile de corpuri care se atrag.

Considerand doua corpuri care de mase egale cu unitatea, situate la o distanta r₁₂, egala cu unitatea, obtinem : F=K. Constanta K este numeric egala cu forta de atractie dintre doua mase unitate, ce se gasesc la distanta egala cu unitatea una fata de cealalta. In sistemul SI valoarea sa masurata este K = 6,66 10^-11 Nm² /kg.

L

d F_L

P

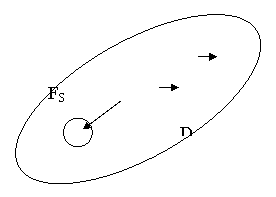
Datorita valorii mici a lui K, forta de atractie dinre doua corpuri de pe suprafata Pamantului este mica, determinarea ei experimentala este dificila. Atractia Pamantului este insa importanta, datorita masei mari a acestuia. Forta cu care Pamantul atrage un corp determina in principal greutatea acelui corp. Pentru un corp de masa m, situat la suprafata Pamantului, neglijand efectele de rotatie diurne a Pamantului se poate scrie egalitatea

deci acceleratia gravitatiei g₀ , la suprafata Pamantului, este

Masurand pe g ₀ , si stiind ca raza R a Pamantului este cam de 6400 km, putem obtine masa Mp a planetei noastre,

Cand corpul de masa m se gaseste la altitudinea h de suprafata Pamantului, distanta de la corp la centrul Pamnantului este R+h, relatia devine

unde g ₀ reprezinta acceleratia gravitatiei la altitudinea h.

Se obtine

Relatia de mai dus ne arata ca acceleratia gravitatiei scade cu altitudinea. aceasta inseamna ca greutatea unui corp nu este de fapt constanta, asa cum eram obisnuiti sa o consideram, ci variaza cu altitudinea. Totusi, pentru corpuri care cad pe Pamant de la o inaltime h, mult mai mica decat raza Pamantului R, putem considera pe g_h constant in tot timpul caderii. Intr-adevar, termenul 1/1+h /R 1- h/R, pentru h/R << 1, deci

unde am neglijat din nou termenul in h²/R². Introducand ultima relatie obtinem

g_h = g ₀ (1-2h/R).

Folosind ultima formula, sa calculam acceleratia gravitatiei la inaltimea h=1 km, avind in vedere ca R 6400 km:

g _h = 1km = g₀ (1-2/6400) = g ₀ (1-1/3200).

Daca neglijam pe 1/3200 fata de 1, nu facem o eroare prea mare, astfel ca putem considera ca g_h = 1 km g₀ si deci acceleratia gravitatiei, ca si greutatea, sunt practic constante in tot cursul caderii corpului de la altitudinea de 1 km. Daca h < R, insa de acelasi ordin de marime, nu mai pot fi neglijati termenii continand puteri superioare ale lui h/R, nu mai este valabila dezvoltarea.

Daca in fiecare punct dintr-o anumita regiune a spatiului se exercita o forta, spunem ca in acea regiune exista un camp de forte. Astfel forta de atractie a Pamantului se exercita in fiecare punct in jurul sau. Spunem atunci ca Pamantul creeaza un camp de forte gravitationale sau, mai pe scurt, un camp gravitational sau gravific.

Dupa cum am vazut, toate corpurile din Univers exercita forte de atractie asupra celorlalte corpuri. Din acest motiv trebuie sa consideram ca fiecare corp da nastere unui camp gravific intr-o anumita regiune a spatiului. Putem spune ca masa fiacarui corp exprima nu numai proprietatile sale inertiale, dar si proprietatile sale gravifice.

Asupra unui corp de masa m ce se gaseste in punctul M actioneaza forta gravifica :

M

M_pm

F = -K r M

r³

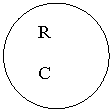
Dupa cum se observa din figura, vectorul r este dirijat de la C la M. Marimea acestei forte nu depinde numai de masa m_p a Pamantului ce creeaza campul gravific, ci si de marimea a masei corpului ce se gaseste in camp. Vrem sa introducem o marime care sa caracterizeze doar proprietatile campului gravific al Pamantului, fara sa depinda de caracteristicile corpurilor ce se afla in acest camp. O astfel de marime ne-ar permite sa comparam inte ele diferite campuri gravifice. Pentru aceasta consideram actiunea diverselor campuri asupra aceleiasi mase, luata drept masa etalon. Cu cat forta care actioneaza asupra masei etalon este mai mare, cu atat campul respectiv este mai intens. Conventional s-a luat drept masa etalon unitatea de masa, adica m=1kg in SI. Marimea

se numeste intensitatea campului grafic al masei m_p ; cu cat modulul acestui vector este mai mare, cu atat actiunea campului asupra unei mase este mai puternica.

Din definitia data se vede ca T are aceeasi expresie ca si acceleratia gravitatiei g, semnificatia sa fizica fiind alta : vectorul G ne da forta cu care campul actioneaza asupra unitatii de masa.

In figura anterioara este reprezentata intensitatea campului gravitational al Pamantului, care are acelasi modul in punctele egal departate de centrul pamantului, adica de suprafata unei sfere cu centrul in C. Din acest motiv se spune caG are simetrie sferica.

Proprietati ale atractiei universale

Legea atractiei universale a fost formulata -si este riguros valabila- pentru puncte materiale. Soarele, planetele, Luna, nu sunt puncte materiale, ci corpuri cu dimensiuni finite. Dar legea atractiei se poate aplica si in acest caz, deoarece Newton a aratat ca:

-Doua corpuri sferice omogene (cu densitatea r=const.), se atrag ca si cum masele lor ar fi concentrate in centrele lor (adica, se atrag ca doua puncte materiale).

-Doua corpuri sferice cu distributie sferica a densitatii (r r(r)), se atrag ca si cum masele lor ar fi concentrate in centrele lor.

In prima aproximatie, corpurile ceresti se pot considera sferice si cu distributie sferica a densitatii. Acest fapt, precum si faptul ca distantele corpurilor ceresti sunt (in general) mult mai mari decat dimensiunile lor, permit ca, in prima aproximatie, sa se aplice legea atractiei universale sub forma

Abaterile de la forma sferica si de la distributia sferica a densitatii, vor produce

anumite perturbatii in miscarea studiata cu forta. F.

Legea atractiei universale, a lui Newton, este una din cele mai importante legi

ale naturii. Atractia are cateva proprietati remarcabile, si anume:

Atractia actioneaza intre toate corpurile Universului, oricat de indepartate ar fi ele (dupa cunostintele actuale).

Fortele de atractie depind de asezarea reciproca a corpurilor. Daca asezarea se schimba, se schimba si fortele.

Fortele de atractie nu depind de compozitia chimica, starea fizica sau de diferitele proprietati ale corpurilor, ci numai de masele lor.

Atractia este o forta pentru care nu exista nici o bariera (nu poate fi ecranata, slabita etc.).

Demonstrarea acestor afirmatii se face in cursurile de Mecanica teoretica pe baza notiunii de potential newtonian.

Natura gravitatiei, esenta ei fizica, nu este pana in prezent lamurita. Conform teoriei relativitatii generale a lui Einstein (numita si teoria gravitatiei) - atractia (gravitatia) este o manifestare a proprietatilor spatio- temporale ale lumii materiale. Ea este o proprietate primara a materiei, proprietate care sta la baza tuturor miscarilor si, dupa esenta ei, este identica cu inertia.