Calculul entropiei conventionale

Calculul entropiei conventionale

Principiul al treilea permite astfel calculul entropiei unei substante la temperatura T, din date calorimetrice, prin ecuatia cunoscuta:

sau la presiune constanta:

Prin integrare, pentru o serie de transformari de faza ale substantei intre 0 K si temperatura T (transformari polimorfe, topire, vaporizare), se obtine ecuatia generala a entropiei la temperatura T:

  (XV.6)

Capacitatile calorice la presiune constanta si caldurile de transformare sunt masurabile pana la 10 K. Entropia unui cristal la temperatura T (intre 10 si 20 K) este data de relatia , conform legii lui Debye, care arata ca in apropierea lui zero absolut C_p = C_v = aT³, unde a este o constanta.

Astfel, primul termen din ecuatia (XV.6) devine:

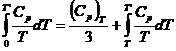
Integralele din ecuatia (XV.6) se obtin grafic din diagrame sau C_p - lnT. Pentru calculul entropiei unui gaz in starea standard (S⁰), gaz perfect la 1 atm, se utilizeaza corectia de gaz perfect dedusa din ecuatia lui Berthelot (v. problema XVI.15):

Valoarea acestei corectii este de ordinul 0,1 u.e.

Valoarea entropiei se poate determina si din date spectroscopice.

Exemplul 4 Sa se arate ca, aplicand ecuatia capacitatii calorice a lui Debye, entropia unui cristal perfect la temperatura foarte scazuta T (10-20 K) este egala cu .

Rezolvare:

Deoarece in apropiere de 0 K, C_P = C_V = aT³, ecuatia:

se poate scrie:

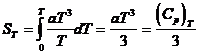
Exemplul 5 Curba din (fig. XV.2) reprezinta variatia cu temperatura a capacitatii calorice molare a oxalatului de calciu, intre 19,31 si 251 K.

Sa se determine entropia oxalatului de calciu la 251 K.

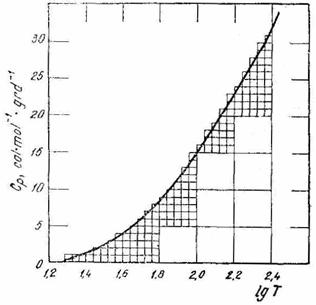
Fig. XV.2. Diagrama capacitatii calorice

molare a oxalatului de calciu

Rezolvare:

Variatia de entropie intre 19,31 si 251 K este data de expresia:

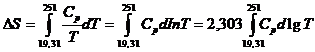
care se rezolva grafic. Numarul de patratele de sub curba, intre lg 19,31 (=1,286) si lg 251 (=2,400), este obtinut prin numarare directa: 340 patratele.

Deoarece fiecare patratel are ca latura verticala o unitate si ca latura orizontala 0,04 unitati, suprafata patratelului este 0,04 unitati:

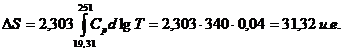
Deoarece entropia la 251 K este:

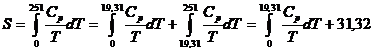
trebuie cunoscuta valoarea primei integrale. Integrala se poate evalua cu o suficienta exactitate (±0,05 u.e.) prin legea lui Debye. 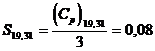u.e. (v. exemplul XV.4).

Prin urmare: S = 0,08 + 31,32 = 31,40 u.e.

Exemplul 6. La temperaturi joase fosfina are mai multe modificatii cristaline. Deasupra temperaturii 49,43 K este stabila forma α. Prin racire lenta, sub 49,43 K, se obtine forma β, iar prin racire rapida sub 30,29 K, forma γ (metastabila).

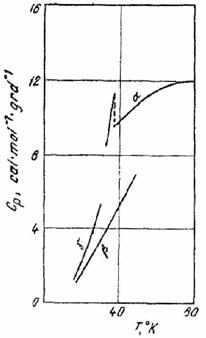
Fig. XV.3. Diagrama capacitatii

calorice molare a fosfinei

Pe baza datelor de mai jos si a diagramei capacitatii calorice din (fig. XV.3), sa se verifice principiul al treilea, calculand entropia α - fosfinei la 49,43 K.

Temperatura de tranzitie: 49,43 K

Caldura de tranzitie: 185,7 cal · mol^-1

Temperatura de tranzitie: 30,29 K

Caldura de tranzitie: 19,6 cal · mol^-1

Rezolvare:

Tabela entropiei α - fosfinei, la 49,43 K, prin cele doua metode: transformarea si transformarea .

In primul caz, :

Temperatura                           S

0-15 K (extrapolare)               0,338

15-49,43 K (grafic)                  4,041

49,43 K      3,757

S_{49,43 K; α - fosfina}                           8,14 u.e.

In al doilea caz, :

Temperatura                           S

0-15 K (extrapolare)               0,495

15-30,29 K (grafic)                  2,185

30,29 K      0,647

30,29-49,43 K (grafic)            800

S_{49,43 K; α - fosfina}                           8,13 u.e.

Rezultatul obtinut arata ca cele doua forme β  si γ au aceeasi entropie la 0 K.

Sa se stabileasca daca utilizarea formei γ metastabila este in contradictie cu enuntarea principiului al treilea in ultima forma ( §2).

Exemplul 7. O metoda de verificare a principiului al treilea consta in compararea valorilor variatiei de entropie a unei reactii chimice, calculate din valorile entropiilor individuale si din datele de echilibru (de exemplu, constanta de echilibru si forta electromotoare a pilelor).

Sa se verifice principiul al treilea in cazul sistemului Ag(s), Cl₂(g), AgCl(s), cunoscand ca f.e.m. standard a pilei:

in care are loc reactia este 1,136 V la 298,16 K.

Rezolvare:

Conform ecuatiei cunoscute, se obtine:

si pentru 298,16 K rezulta:

In tabelele termochimice se gaseste . Prin urmare:

Mai exact, cunoscand coeficientul de temperatura al f.e.m:

se obtine, conform ecuatiei (XIV.31):

Pe baza valorilor entropiilor individuale (din tabele) se calculeaza:

(valoarea exacta este).

Concordanta este, deci, foarte buna.   

PROBLEME

1. Sa se calculeze entropia n-heptanului lichid la 298,1 K, cunoscand valorile capacitatii calorice molare la presiune constanta, la diferite temperaturi:

La temperatura de topire (182,5 K) entalpia de topire este 3356 cal · mol^-1.

2. Prin legea lui Debye si integrare grafica, entropia hidrazinei in stare solida la temperatura de topire (+1,53 ^oC) este 16,05 u.e. Caldura de topire la +1,53 ^oC este .

Capacitatea calorica a hidrazinei in stare lichida, intre 1,53 si 25 ^oC, este C_p = 23,37 + 0,014(T - 280) cal · mol^-1 · grad^-1.

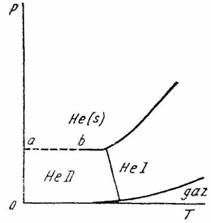
Fig. XV.4. Diagrama de echilibru a heliului

Fig.XV.5. Diagrama coeficientului

de dilatatie a heliului (l)

Caldura de vaporizare la +25 ^oC este .

Presiunea de vapori este data de ecuatia:

Sa se calculeze entropia hidrazinei la 1 atm si 25 ^oC, in stare de gaz perfect.

3. Diagrama de echilibru a heliului este de forma indicata in (fig. XV.4).

Sa se arate ca, in conformitate cu principiul al treilea, curba ab este perpendiculara pe axa ordonatelor.

4. Diagrama din (fig. XV.5) reprezinta variatia coeficientului de dilatatie α, cu temperatura, pentru He I si He II (in domeniul temperaturilor foarte scazute).

Sa se constitue trasarea curbei α catre T = 0 K si sa se justifice forma curbei.

5. Sa se discute metodele de verificare experimentala a principiului al treilea (v. exemplele XV.3, XV.6, XV.7 si problemele XV.10 si XV.11).

6. Sa se verifice relatia:

valabila pentru saruri binare, in care V_i este volumul molecular calculat din raze ionice.

7. Sa se verifice relatiile valabile pentru combinatii organice:

a) solide: S₂₉₈ = 1,1 C_p (la 298 K);

b) lichide: S₂₉₈ = 1,4 C_p (la 298 K).

8. Pe baza tabelelor de constante termodinamice sa se calculeze variatiile de entropie in reactiile de formare a hidratilor cristalini:

A_mB_n(s) + xH₂O(s) =A_mB_nxH₂O(s)

si sa se interpreteze rezultatul.

9. Sa se arate ca, pentru 0 K, se verifica ecuatia C_p - C_V = 0.

10. Sa se calculeze entropia mercurului la 0 K, cunoscand urmatoarea compozitie izotopica:

¹⁹⁶Hg    ²⁰¹Hg

¹⁹⁸Hg    ²⁰²Hg

¹⁹⁹Hg    ²⁰⁴Hg

²⁰⁰Hg   

Este posibila o valoare (pozitiva) mai mare sau mai mica decat valoarea calculata prin ecuatia cunoscuta a entropiei de amestec?

11. Se stie (cap. VIII) ca tensiunea superficiala scade cu temperatura dupa o curba analoaga ca forma cu cea din (fig. XV.6). Sa se arate ca, in domeniul temperaturilor mici, curba γ(T) devine perpendiculara pe axa ordonatelor.

Fig. XV6. Variatia tensiunii

superficiale cu temperatura

12. Pe baza diagramei capacitatii calorice molare a acidului clorhidric (fig. XV.7) si a datelor de mai jos, sa se calculeze entropia acidului clorhidric (gaz perfect) la temperatura de fierbere. Valoarea calculata din date spectroscopice (v.vol. II) este 41,45. u.e.

a) Tranzitia HCl(s₁) → HCl(s₂)

temperatura 98,36 K

caldura de tranzitie 284,3 cal · mol^-1

b) Topire HCl(s₂) → HCl(l)

temperatura 158,91 K

caldura de topire 476 cal · mol^-1

c) Vaporizare HCl(l) → HCl(g)

temperatura 188,07 K

caldura de vaporizare 3 860 cal · mol^-1

13. Pe baza principiului al treilea, la 298,16 K, pentru reactia Mg(OH)₂(s) = MgO(s) + H₂O(g), se obtine din calcule o variatie de entropie

Fig. XV.7. Capacitatea calorica molara a Hcl

Valoarea determinata experimental din date de echilibru si caldura de reactie este

Sa se explice diferenta intre cele doua valori.

*14. Sa se arate ca expresia caldurii specifice valabila la temperaturi joase:

c = aT^b

b trebuie sa fie mai mare decat unitatea.

*15. Enuntarea principiului al treilea se face si sub forma: este imposibil de a cobori temperatura unui sistem la 0 K printr-un numar finit de operatii. Sa se arate ca acest enunt rezulta din expresia: .