SUBIECTE DATE LA EXAMENELE DE FIZICA ALE ANULUI II, FACULTATEA DE ENERGETICA A I.P.B., februarie 1985

136. Pornind de la legea lui Planck a radiatiei termice, sa se determine lungimea de unda pentru care puterea spectrala de emisie (densitatea spectrala a emisivitatii) a corpului negru atinge un maxim, in cazul in care temperatura suprafetei corpului negru . Pentru ce lungime de unda se realizeaza maximul curbei de emisie , daca temperatura suprafetei corpului negru scade cu 1000 K? Se dau: si

137. Cunoscand energia a fotonului incident intr-un act elementar de imprastiere (difuzie) neelastica Compton si unghiul format de directia miscarii electronului de recul cu directia deplasarii fotonului incident, sa se determine: a) lungimea de unda a fotonului Compton difuzat; b) lungimea de unda de Broglie asociata electronului de recul.

138. O particula  de masa m se gaseste intr-o groapa de potential bidimensionala: pentru si , respectiv pentru valori ale coordonatelor x,y care nu satisfac una sau ambele conditii de mai sus. Stiind ca , iar , se cere: a) sa se calculeze energia primelor 2 nivele energetice pentru un electron () aflat in interiorul gropii de potential; b) sa se verifice daca sunt indeplinite in acest caz relatiile de nedeterminare ale lui Heisenberg.

139. Un fascicul de particule se deplaseaza in regiunea x.0 dupa directia si in sensul pozitiv al axei 0x, cu energia cinetica E_c. Stiind ca particulele se deplaseaza intr-un camp de forte descris de potentialul pentru , respectiv pentru (unde ), sa se deduca expresiile functiei de unda corespunzand domeniilor , respectiv , si sa se interpreteze rezultatul obtinut.

140. a) Sa se construiasca schema tranzitiilor de structura fina intre nivelele n=3 si n=2 ale hidrogenului atomic; b) Sa se calculeze deplasarile frecventelor componentelor Zeeman ale tranzitiilor , in cazul in care atomii de hidrogen se gasesc intr-un camp magnetic extern cu inductia B=2T. Se dau: si

141. Un sistem fizic este format din 3 particule identice, care pot fi repartizate pe nivelele energetice si , carora le corespund ordinele de degenerare si . Sa se stabileasca modalitatile de dispunere a particulelor pe cele 3 nivele si probabilitatile relative de realizare - la temperatura T a fiecarei dispuneri - daca particulele sunt: a) bozoni, b) fermioni.

142. Izotopul RaA se dezintegreaza, cu durata de injumatatire minute, formand izotopul RaB care se dezintegreaza la randul sau, cu durata de injumatatire minute. Stiind ca, initial, preparatul continea numai izotopul RaA, sa se determine durata dupa care cantitatea de radioizotop RaB va fi maxima.

D. SUBIECTE DATE LA FAZA NATIONALA A CONCURSULUI PROFE-SIONAL-STIINTIFIC STUDENTESC DE FIZICA (11-13 mai 1984, Univ. Timisoara)

Anul I, invatamant universitar (facultati de Fizica)

143. Un cilindru de masa m si de raza R are centrul de masa situat intr-un punct aflat la distanta de axa cilindrului si momentul de inertie I fata de aceasta axa. Cilindrul este asezat pe un plan orizontal suficient de rugos. Care va fi perioada micilor oscilatii ale cilindrului in jurul pozitiei de echilibru?

144. Caldura molara a unui gaz ideal variaza dupa legea , unde a=cons-tant, intr-un anumit proces. Sa se afle: a) lucrul mecanic efectuat de n moli de gaz in acest proces daca temperatura variaza de la T₁ la T₂; b) ecuatia procesului in coordonate (p,V).

145. Un vas umplut cu aer, initial neionizat, aflat in conditii normale, este iradiat cu un fascicul de raze X care ionizeaza o mica parte din moleculele aflate in interior. Ionii negativi sunt moleculele de O₂ cu un electron suplimentar. Masa molara a aerului este M=29 kg*kmol^-1. Dimensiunile vasului sunt , peretii sunt din metal, iar restul din material izolator. Intre peretii conductori se aplica o tensiune U care da nastere unui curent electric de intensitate I. Viteza medie a ionilor este , iar drumul liber mediu este . Sa se afle: a) timpul mediu intre ciocniri, b)conductivitatea electrica a acestui gaz slab ionizat, c) ce fractiune din numarul moleculelor gazului este ionizata.

Anul II, invatamant universitar (facultati de Fizica)

146. Un fascicul ingust de lumina paralela cade pe o sfera de raza R si indice de referinta n, dupa directia unui diametru . In ce conditii se va focaliza fasciculul in afara sferei? Sa se determine pozitia focarului fata de centrul sferei.

147. Folosindu-se regula de cuantificare Bohr-Sommerfeld: , sa se determine valorile proprii ale energiei unei particule de masa m care se misca: a) intr-o groapa de potential unidimensionala cu largimea L si cu peretii de inaltime infinita, b) liber, pe un cerc de raza r, c) intr-un camp potential unidimensional , unde a este o constanta pozitiva, d) de-a lungul unei orbite circulare intr-un camp central in care energia potentiala a particulei este , a fiind o constanta pozitiva.

T57. Se da un dispozitiv Young plasat in apa. In vecinatatea unei fante se afla o bula cu aer. Sa se explice ce se intampla cu sistemul de franje.

T58. Analizati critic metodele de determinare experimentala a constantei lui Planck.

Anul I, invatamant tehnic superior

T59. Spatiul fazelor. Teorema lui Liouville.

148. Poate un foton cu energia de 0,9 MeV sa se scindeze intr-o pereche electron-pozitron a caror masa de repaus este (pentru fiecare dintre ele) ? Justificati raspunsul.

T60. Miscarea oscilatorie fortata (intretinuta). Rezonanta mecanica.

149. O sursa aflata intr-un mediu elastic emite unde plane de forma . Lungimea de unda a undelor longitudinale este . Se cere: a)dupa cat timp va incepe sa oscileze un punct situat la distanta fata de sursa; b) stiind ca densitatea mediului elastic este , sa se calculeze intensitatea  undei si nivelul intensitatii sonore. Intensitatea corespunzatoare pragului inferior de audibilitate este ; c) sa se scrie ecuatia undei de presiune.

150. O sursa de lumina emite impulsuri cu perioada T₀ in referentialul propriu. Sursa se deplaseaza cu viteza v, observatorul aflandu-se pe directia care face un unghi cu directia de miscare. Se cere: a) sa se calculeze frecventa receptionata de observatorul situat foarte departe de sursa; b) se considera un satelit care se misca cu viteza la distanta r de sol. Un oscilator aflat pe satelit emite un semnal cu perioada proprie T₀. Sa se arate cum variaza frecventa receptionata in functie de pozitia satelitului, stiind ca la statia de receptie exista un oscilator identic cu cel de pe satelit.

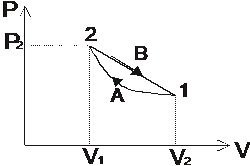151. Un kilomol de gaz perfect monoatomic parcurge ciclul din figura, format din adiabata 1A2 si procesul reprezentat in diagrama (p,V) de dreapta 2B1. Cunoscand parametrii starii 2 (adica V₂ si p₂), raportul de compresie si indicele adiabatei al gazului, sa se determine randamentul motorului termic care ar functiona dupa acest ciclu. Sa se discute solutia problemei.

Anul II, invatamant tehnic superior, profil electric

T61. Propagarea undelor electromagnetice in medii ideale (deducerea ecuatiei propagarii si transversalitatea undei).

T62. Relatiile de nedeterminare (incertitudine) ale lui Heisenberg.

T63. Cum se poate obtine lumina polarizata eliptic?

T64. Determinati lungimea de unda de Broglie corespunzand vitezei celei mai probabile a moleculelor unui gaz aflat la temperatura T, masa fiecarei molecule a gazului fiind m.

T65. Ce este structura fina a unei linii spectrale?

152. Stiind ca doua dintre liniile spectrale ale seriei Balmer au lungimile de unda si , sa se determine carei serii spectrale ii corespunde tranzitia al carui numar de unda este egal cu diferenta numerelor de unda ale celor doua linii. Se da constanta Rydberg:

153. Se considera o groapa de potential infinita unidimensionala pentru pentru Sa se determine: a) media  a coordonatei particulei, b) media cantitatii .

154. Sa se determine energia cea mai probabila a unei