Alegerea si acordarea algoritmilor de reglare a motorului de curent continuu

Algoritmii de reglare s-au ales mai intai dupa metodele clasice, care se aplica sistemelor conventionale continue, respectiv criteriul modulului si proiectarea  directa dupa perturbatie, din care au rezultat algoritmii PID continue.

Acesti algoritmi de reglare vor fi discretizati alegand o perioada de discretizare  mica in comparatie cu consatanta de timp a procesului

T=T_f /100 T=0.001 [s]

rezultand algoritmi de reglare PID discreti cuasicontinui.

1.1. Proiectarea regulatorului R de pe calea directa

1.1.1. Proiectarea regulatorului cu functia de transfer H_R(s) in varianta analogica se face dupa criteriul modulului, varianta Kessler astfel obtinand un regulator tip PI:

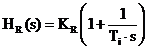
Parametrii de acord optimi ai regulatoarelor sunt:

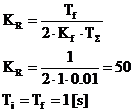
Parametrii care dau performantele sistemului de reglare sunt:

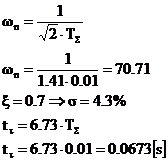
Pentru: R(s)=1/s, rezulta:

Pentru: R(s)=1/2·s, rezulta:

Pentru o reglare numerica a procesului se considera un algoritm incremental PI obtinut prin discretizarea algoritmului PI analogic al regulatorului, de forma:

unde:

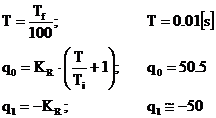
Efectuand inlocuirile:

Schema de implementare a algoritmului numeric este de forma:

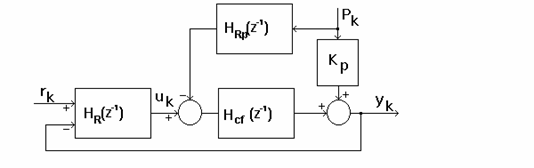
Figura 9.1 - schema de implementare

1.1.2. Proiectarea regulatorului cu functia de transfer H_R(z^-1) in varianta numerica se poate realiza si dupa algoritmul Dead - Beat

Consideram un sistem numeric de reglare. Functia de transfer discretizata este:

;

Acest algoritm asigura un raspuns asimptotic stabil al sistemului pe baza compensarii polilor procesului. Se considera sistemul caracterizat prin functia de transfer:

H₀ (z^-1) = p₁ · z^-1 + p₂ · z^-2 +..+ p_m ·z^-m ;

Raspunsul asimptotic stabil la o intrare treapta se obtine daca este satisfacuta conditia:

p₁+ p₂ +..+ p_m=1;

regulatorul furnizeaza pentru aceeasi intrare

comanda:

u (z^-1) = u₀ + u₁ · z^-1 + u₂ · z^-2 +..+ u_m · z^-m-1 ;

Notand:

Q(z^-1) =  = u₀ + ( u₁ -u₀ ) · z^-1+.+ ( u_m -u_m-1 ) · z^-m =

= q₀ + q₁ · z^-1 + q₂ · z^-2 +.+ q_m · z^-m;

se obtine:

;

deoarece:

si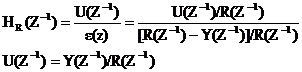

Cu ajutorul acestor relatii se poate determina parametrii regulatorului cu relatiile:

q_i = q₀a_i ;( i = 1.m_a );

p_j= q₀ · b_i ; ( j = 1.m_b );

din conditia de mai sus, care echivaleaza cu prezenta componentei integrale, se obtine:

;

Algoritmul poarta denumirea de algoritm Dead-Beat.

Comanda initiala depinde de parametrii procesului. Comanda initiala u₀=q₀ este detreminata de coeficientii b_j ai modelului procesorului, si in anumite cazuri pate rezulta cu valori mari.

In cazul optimizarii comenzii ( U_opt ) oscilatiile comenzii dispar in regim stationar.

Aplicand algoritmul de Dead-Beat pentru functia de transfer :

;

a₁=-1,3579; b₁=0,0037;

a₂= 0,3642; b₂=0,0026;

alegand factorul de amplificare K_m=1:4000, obtinem:

Utilizand algoritmul Dead-Beat pentru functia de transfer discretizat se obtine functia de transfer al regulatorului (care asigura algoritmul):

1.2. Testarea buclei de reglare dupa referinta

Schema de testare a buclei de reglare dupa referinta care contine regulatorul R pe calea directa e prezentata in figura urmatoare:

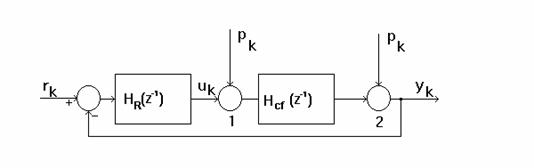
Figura 9.2 - schema de testare a regulatorului R

Plecand de la schema din figura 3. si apeland la procedurile din mediul de programare MATLAB se determina urmatoarele performante ale SRA:

1.   raspunsul sistemului Y_k(t) pentru o intrare de tip treapta unitara r_k=1/(1-z);

2.   comanda u_k(t) pentru intrarea treapta unitara;

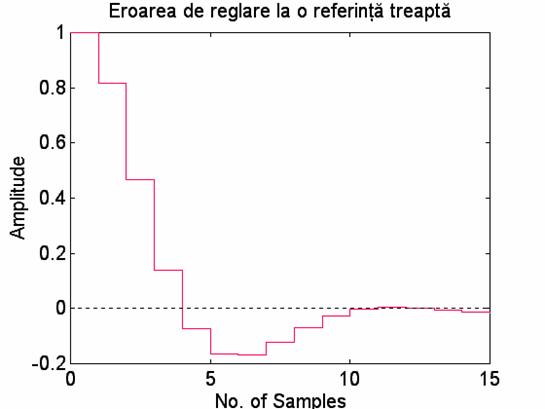
3.   eroarea e_k(t) pentru intrarea treapta unitara;

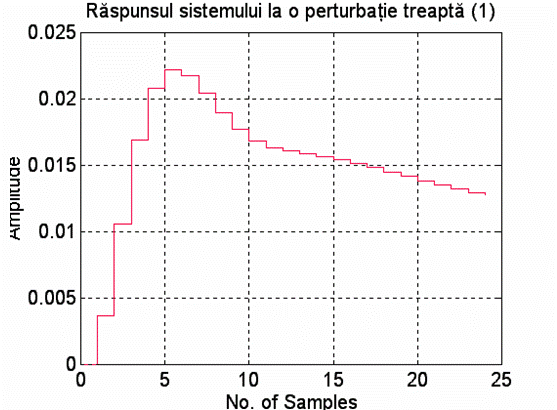
4.   raspunsul sistemului Y^P_k(t) pentru o perturbatie P_k de tip treapta unitara aplicata succesiv in punctul 1 si 2.

1.3. Proiectarea regulatorului dupa perturbatie (RP)

Proiectarea regulatorului RP de face pe baza metodei clasice de proiectare dupa perturbatia masurabila a sistemelor continue:

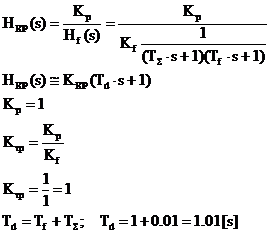
Regulatorul RP este necauzal (tip PD). Pentru imbunatatirea performantelor SRA de tip derivativ se va alege un regulator cauzal de tip PD cu filtrare, avand urmatoarea functie de transfer:

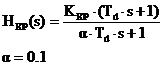
Discretizand algoritmul de mai sus prin metoda trapezelor, respectiv introducand in aceasta relatie aproximatia urmatoare:

                                 

1.4. Testarea buclei de reglare dupa perturbatie

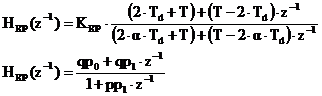
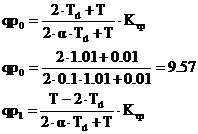
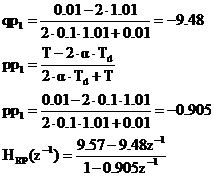
Schema de testare a buclei de reglare directa dupa perturbatie este:

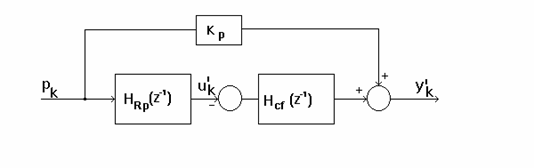
Figura 9.4 - schema de testare dupa perturbatie

Plecand de la figura se va determina urmatoarele performante ale sistemului:

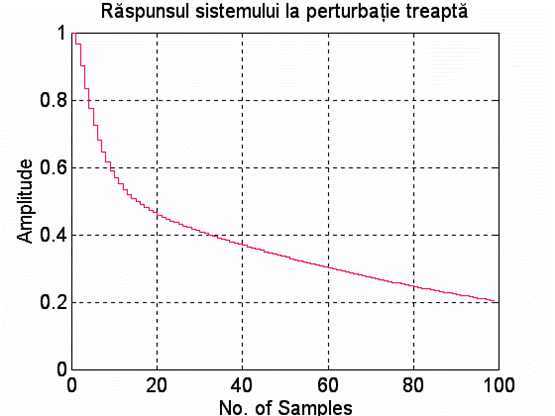
1.   raspunsul sistemului dupa perturbatia treapta unitara Y_pk(t), respectiv rejectia perturbatiei;

2.   raspunsul sistemului Y_pk(t) dupa perturbatia rampa;

3.   raspunsul sistemului Y_pk(t) dupa perturbatia sinusoidala;

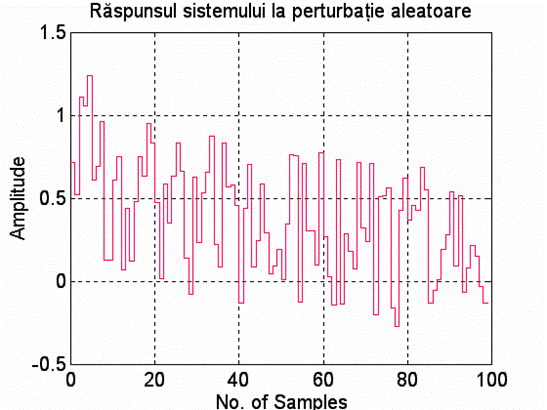
4.   raspunsul sistemului la perturbatie aleatoare.

Pentru testare se va utiliza urmatoarea functie de transfer:

ANEXE

Anexa 1. Testele de verificare rezolvate in MATLAB

1.1.          Programele de verificare a SRA de turatie a MCC

Programul ' pr_mcc1.m ' testeaza sistemul inchis cu si fara filtrare la diferitele semnale de referinta . Semnalele de intrare sunt de tip treapta rampa, sinusoidal.

program_mcc1.m

clear;

clc;

% timpul de testare

t=0:0.001:0.6;

% generarea unui semnal sinusoidal

s=sin(t*150);

% Functia de transfer al filtrului

ts=0.016;

nf=[1];  

mf=[4*ts 1];

% functia de transfer a sistemului inchis (dupa referinta)

n0=[0.00064 0.074 1];

m0=[4.096*10^(-6) 0.002 0.064 1]*0.0033;

% functia de transfer a sistemului inchis cu filtrare

[n0f,m0f]=series(nf,mf,n0,m0);

% trasarea graficelor

figure(1);

step(n0,m0,t);

title('Raspuns la treapta a SRA (fara filtrare)');

pause;

figure(2);

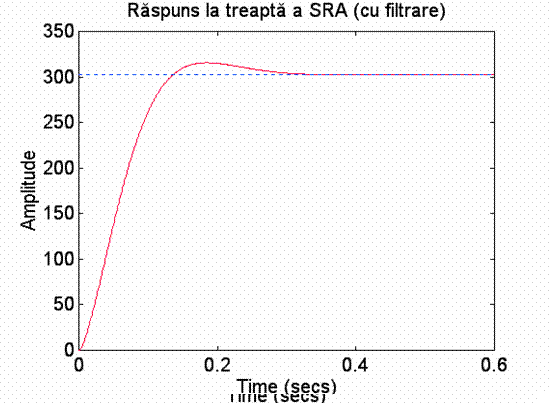
step(n0f,m0f,t);

title('Raspuns la treapta a SRA (cu filtrare)');

pause;

figure(3);

lsim(n0,m0,t',t);

grid;

title('Raspuns la rampa a SRA (fara filtrare)');

pause;

figure(4);

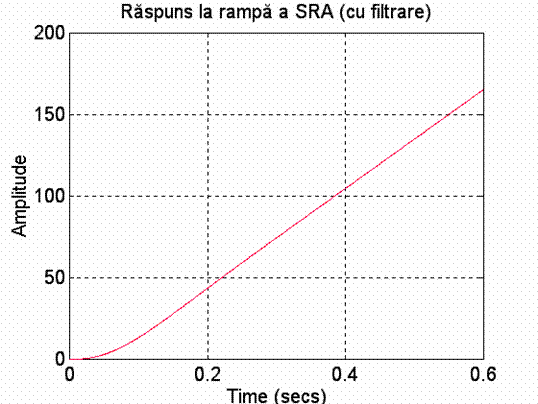
lsim(n0f,m0f,t',t);

grid;

title('Raspuns la rampa a SRA (cu filtrare)');

pause;

figure(5);

lsim(n0,m0,s',t);

grid;

title('Raspuns la semnal sinusoidal a SRA (fara filtrare)');

pause;

figure(6);

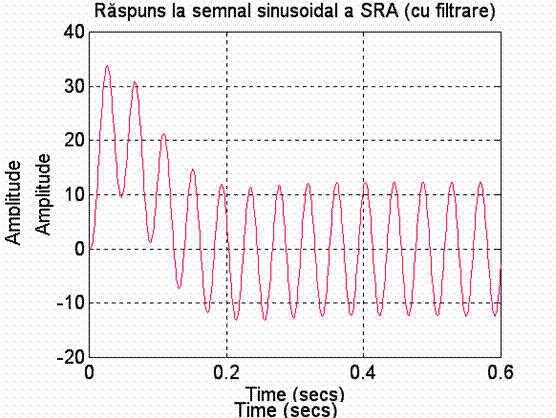
lsim(n0f,m0f,s',t);

grid;

title('Raspuns la semnal sinusoidal a SRA (cu filtrare)');

pause;

close(1);

close(2);

close(3);

close(4);

close(5);

close(6);

Programul ' program_mcc2.m ' calculeaza functia de transfer a sistemului dupa perturbatie si testeaza sistemul la o perturbatie tip treapta:

program_mcc2.m

clear;

clc;

% parametrii MCC

r=0.916;

ke=0.137;

tm=0.52;

% functia de transfer MCC

nm=[r/ke];

mm=[tm 0];

% functia de transfer a sistemului deschis exterior

ts=0.016;

nd=[4*ts 1];

md=conv([8*ts*ts 0 0],[ts 1]);

% calcularea functiei de transfer a sistemului inchis

[n1,m1]=feedback(1,1,nd,md,-1);

[n0,m0]=series(nm,mm,n1,m1);

% trasarea graficului

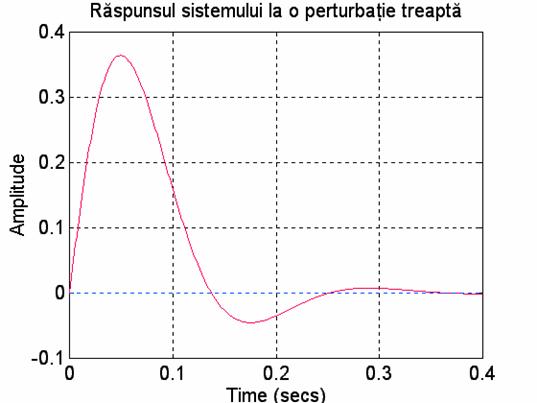
step(n0,m0,0:0.001:0.4);

title('Raspunsul sistemului la o perturbatie treapta');

grid;

pause;

close;

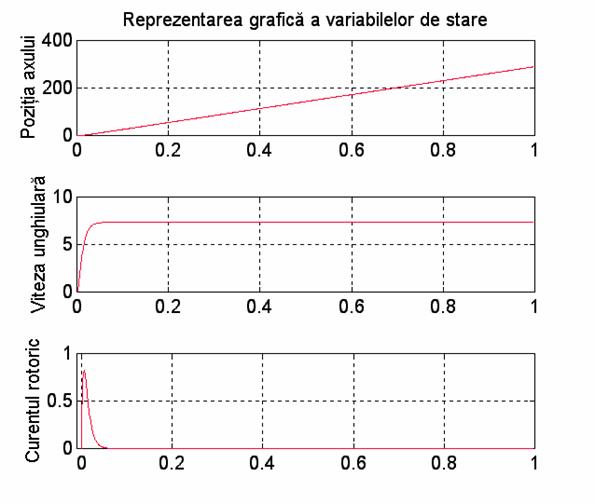
Programul ' program_mcc3.m ' realizeaza trasarea variabilelelor de stare a MCC

program_mcc3.m

clear;

clc;

% matricile sistem

A=[01 0

0012.81

0 -1.31 -8.8 ];

B=[0 0 9.61]';

C=[0 1 0];

D=0;

%t=1:20;

% calcularea starilor

[y,x]=step(A,B,C,D);

% reprezentare grafica

t=(0:length(y)-1)/length(y);

subplot(3,1,1);

plot(t,x(:,1));

title('Reprezentarea grafica a variabilelor de stare');

ylabel('Pozitia axului');

grid;

subplot(3,1,2);

plot(t,x(:,2));

ylabel('Viteza unghiulara');

grid;

subplot(3,1,3);

plot(t,x(:,3));

axis([-0.01 1 0 1]);

ylabel('Curentul rotoric');

grid;

pause;

close;

1.2.          Programele de verificare a SRA a puterii reactive a MS

Programul ' program_ms1.m' discretizeaza partea fixa a procesului respectiv regulatorul de pe calea directa si la o referinta tip treapta calculeaza valoarea iesirii, a erorii de reglare a comenzii, respectiv la perturbatii treapta iesirea sistemului.

program_ms1.m

clc;

clear;

% functia de transfer continua

tf=1;

ts=0.01;

nc=[1];

mc=conv([tf 1],[ts 1]);

% discretizarea functiei de transfer

h=tf/100;

[a,b,c,d]=tf2ss(nc,mc);

[fi,gamma,cd,dd]=c2dm(a,b,c,d,h,'zoh');

[nd,md]=ss2tf(fi,gamma,cd,dd);

% discretizarea regulatorului

n=[50 50];

m=[1 0];

[a,b,c,d]=tf2ss(n,m);

[aa,bb,cc,dd]=c2dm(a,b,c,d,0.021,'zoh');

[nr,mr]=ss2tf(aa,bb,cc,dd);

% TRASAREA GRAFICELOR

% in-r out-y

[n1,m1]=series(nd,md,nr,mr);

[n2,m2]=cloop(n1,m1,-1);

figure(1);

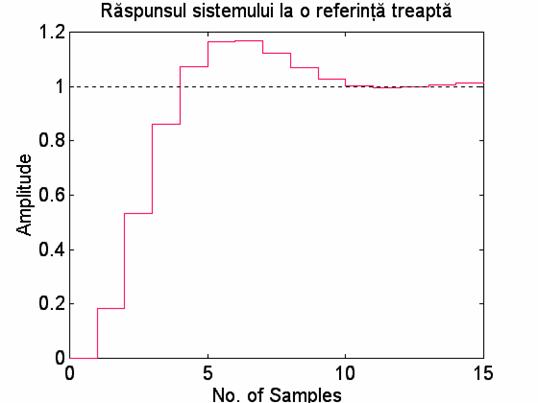
dstep(n2,m2,16);

title('Raspunsul sistemului la o referinta treapta');

pause;

% in-r out-eps

[n1,m1]=series(nd,md,nr,mr);

[n2,m2]=feedback(1,1,n1,m1,-1);

figure(2);

dstep(n2,m2,16);

title('Eroarea de reglare la o referinta treapta');

pause;

% in-r out-u

[n1,m1]=feedback(nr,mr,nd,md,-1);

figure(3);

dstep(n1,m1,16);

title('Comanda la o referinta treapta');

pause;

% in-p1 out-u

[n1,m1]=feedback(nd,md,nr,mr,-1);

figure(4);

dstep(n1,m1,25);

grid;

title('Raspunsul sistemului la o perturbatie treapta (1)');

pause;

% in-r out-eps

[n1,m1]=series(nd,md,nr,mr);

[n2,m2]=feedback(1,1,n1,m1,-1);

figure(5);

dstep(n2,m2,16);

title('Raspunsul sistemului la o perturbatie treapta (2)');

pause;

close(1);

close(2);

close(3);

close(4);

close(5);

Programul ' program_ms2' realizeaza calcularea functiei transfer discretizate a SRA de a puterii reactive a unui MS si testarea sistemului la perturbatii

program_ms2.m

clc;

clear;

% functia de transfer continua

tf=1;

ts=0.01;

nc=[1];

mc=conv([tf 1],[ts 1]);

% discretizarea functiei de transfer

h=tf/100;

[a,b,c,d]=tf2ss(nc,mc);

[fi,gamma,cd,dd]=c2dm(a,b,c,d,h,'zoh');

[nd,md]=ss2tf(fi,gamma,cd,dd);

% discretizarea regulatorului

n=[1.01 1];

m=[0.101 1];

[a,b,c,d]=tf2ss(n,m);

[aa,bb,cc,dd]=c2dm(a,b,c,d,0.021,'tustin');

[nr,mr]=ss2tf(aa,bb,cc,dd);

% construirea sistemului;

[n1,m1]=series(nr,mr,-1,1);

[n2,m2]=series(n1,m1,nd,md);

[n0,m0]=parallel(1,1,n2,m2);

% trasarea raspunsurilor

% raspunsul sistemului la treapta

figure(1);

dstep(n0,m0,100);

grid;

title('Raspunsul sistemului la perturbatie treapta');

pause;

% raspunsul sistemului la rampa

t=0:100;

t=t';

figure(2);

dlsim(n0,m0,t');

grid;

title('Raspunsul sistemului la perturbatie rampa');

pause;

% raspunsul sistemului la un semnal aleator

for i=1:100

r(i)=0.5+rand(0.5);

end;

figure(3);

dlsim(n0,m0,r');

grid;

title('Raspunsul sistemului la perturbatie aleatoare');

pause;

% raspunsul sistemului la un semnal sinusoidal

t=0:0.001:0.3;

s=sin(t*90);

figure(4);

dlsim(n0,m0,s');

grid;

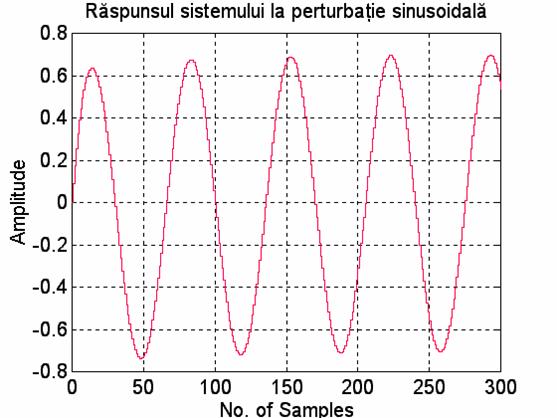
title('Raspunsul sistemului la perturbatie sinusoidala');

pause;

close(1);

close(2);

close(3);

close(4);

Programul ' program_ms3.m ' realizeaza testarea regulatorului dupa perturbatie la o intrare sinusoidala

program_ms3.m

clear;

clc;

tf=1;

ts=0.01;

nc=[1];

mc=conv([tf 1],[ts 1]);

% discretizarea functiei de transfer

h=tf/100;

[a,b,c,d]=tf2ss(nc,mc);

[fi,gamma,cd,dd]=c2dm(a,b,c,d,h,'zoh');

[nd,md]=ss2tf(fi,gamma,cd,dd);

% discretizarea regulatorului

n=[1.01 1];

m=[0.101 1];

[a,b,c,d]=tf2ss(n,m);

[aa,bb,cc,dd]=c2dm(a,b,c,d,0.021,'tustin');

[nr,mr]=ss2tf(aa,bb,cc,dd);

% construirea sistemului;

[n1,m1]=series(nr,mr,-1,1);

[n2,m2]=series(n1,m1,nd,md);

[n0,m0]=parallel(1,1,n2,m2);

% testarea sistemului

t=0:0.6:150;

s=ones(1,length(t))*0.5;

a=0.5*cos(0.01*pi*t);

y=s+a.*sin(0.3*pi*t);

subplot(211);

plot(t,y);

grid;

title('Forma semnalului de intrare')

subplot(212);

dlsim(n0,m0,y');

grid;

title('Iesirea sistemului');

pause;

close;

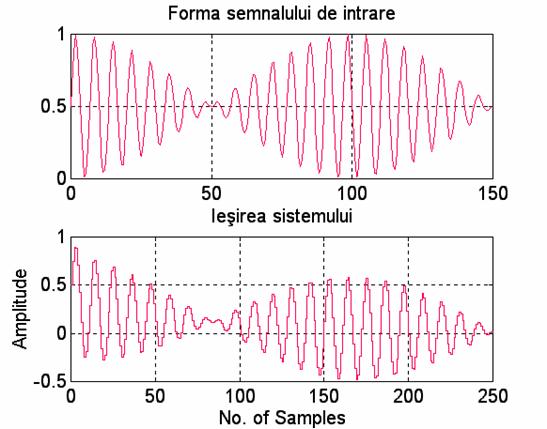
Observatii:

- Intrarea oscileaza in jurul valorii 0.5. Aceasta valoare este readusa la 0 de regulator, deci iesirea oscileaza in jurul valorii 0.

- Amplitudinea oscilatiilor e redusa.

Anexa 2. Raspunsurile obtinute

2.1 

Pentru motorul de curent continuu

2.2.   

Pentru generatorul sincron

Bibliografie

1) Prof. dr. ing. Horatiu Zarnescu Ingineria reglarii automate - Curs

2) Prof. dr. ing. Horatiu Zarnescu Elemente de reglare automata - Curs, 1998