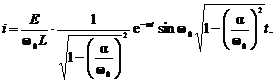Cazuri aparte in studiul circuitelor electrice

In cadrul acestui subcapitol vor fi prezentate cateva situatii mai deosebite care intervin, adeseori, in studiul circuitelor electrice si anume:

- regimul tranzitoriu al circuitelor electrice;

- comportarea circuitelor electrice in radiofrecventa;

- circuite electrice cu parametrii de circuit neliniari;

- reprezentarea circuitelor electrice ca diporti (cuadripoli);

- liniile electrice lungi.

1. Regimul tranzitoriu al circuitelor electrice

Din punctul de vedere al "evolutiei" in timp, regimul electrocinetic al circuitelor electrice (stationar sau nestationar) poate fi permanent si tranzitoriu.

Regimul permanent este acela in care marimile ce caracterizeaza sistemul electrocinetic isi pastreaza mereu aceleasi valori: in regim stationar (de curent continuu) marimile electrice de circuit (t.e.m., tensiunile la borne si curentii) sunt constante in timp, parametrii de circuit au aceeasi valoare (rezistente sau conductante) si structura retelei se pastreaza aceeasi in regim nestationar, marimile electrice de circuit au tot timpul aceeasi forma de unda (cu aceleasi valori maxime si minime, aceleasi valori efective, aceeasi faza initiala si aceeasi pulsatie), iar componentele electrice de circuit, mereu in aceeasi structura, au parametrii de circuit (rezistente/conductante, capacitati/elastante, inductivitati-proprii si mutuale) neschimbati. Daca cel putin una din caracteristicile electrocinetice (insiruite anterior) se modifica, atunci circuitul electric trece la alt regim permanent.

Aceasta trecere de la un regim electrocinetic permanent la alt regim electrocinetic permanent nu se poate face instantaneu, ci numai printr-un regim variabil in timp denumit regim tranzitoriu. "Saltul" de la un regim permanent la altul nu poate fi brusc (de tip treapta) deoarece schimbarea starii permanente duce la modificari ale campurilor electromagnetice aferente circuitului ceea ce implica anumite transferuri de energie electromagnetica, de forma:

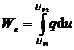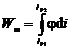- electrica si - magnetica,

(v. § 1.5.3) in care U_P1, U_P2 si I_P1, I_P2 sunt valorile caracteristice ale tensiunilor si curentilor in regimurile permanente 1 si 2 ce "incadreaza" regimul tranzitoriu. Cum un transfer instantaneu al acestei energii (oricat de mici) ar insemna ca derivatele lor in raport cu timpul (dW_{e m}/dt) sa fie infinite, adica un dt=0 sau o putere a sistemului infinita, ceea ce practic nu poate fi posibil, face ca regimul tranzitoriu sa aiba o "anumita" durata. Dupa cum se va vedea mai incolo, durata unui regim tranzitoriu este teoretic infinita (ceea ce ar insemna ca un al doilea regim permanent nu mai este posibil!). Practic, regimul tranzitoriu evoluand de cele mai multe ori exponential dupa un timp -in general- scurt, se ajunge la valori ale marimilor caracteristice starii electrocinetice de 0,90,95 din noul regim permanent. In legatura cu acest fapt, pentru multe sisteme fizice de tip electromagnetic, se defineste un asa-numit timp de stabilire care fixeaza durata regimului tranzitoriu la timpul necesar ca o marime de stare (ce prezinta importanta pentru aplicatia avuta in vedere) sa ajunga la 0,9 din valoarea care (teoretic) va fi luata de acea marime in noul regim permanent.

Ca urmare, din punctul de vedere al definitiilor date, functionarea unui circuit electric poate fi privita ca o insiruire de regimuri permanente si tranzitorii. Desi practic scurt, in unele aplicatii, analiza regimului tranzitoriu este determinanta, rolul ei constand in a exprima cum variaza in timp marimile de stare electrocinetica si ce parametru - timp ii este caracteristic (care, dupa cum se va vedea, se numeste constanta de timp si se noteaza mai intotdeauna cu t

Modele de calcul ale regimului tranzitoriu

O modalitate de descriere a trecerii de la un regim permanent la altul o constituie introducerea unei modificari bruste a unei marimi de stare a circuitului electrocinetic analizat (de pilda conectarea brusca a unei surse electrice cu t.e.m. continua sau sinusoidala). Acest lucru se poate face prin utilizarea functiei treapta unitate a lui Heaviside (v. § 9.1.4) definita astfel:

(TR 1)               ,

unde t este timpul. O astfel de idealizare este intotdeauna justificata atunci cand, pe scara timpului prin care se studiaza fenomenul, durata modificarii (de pilda, durata de actionare a unui contact) este neglijabila. Cand acest semnal este derivat, apare in mod natural derivarea in punctul de discontinuitate, ceea ce implica aplicare unor elemente de teoria distributilor.

In principiu calculul circuitelor electrice in regim tranzitoriu se face cu ajutorul teoremei lui Ohm generalizate (v.subcap.8.4) si al teoremelor lui Kirchhoff in curent variabil. Acestea, in functie de structura circuitului, conduc la o ecuatie sau la un sistem de ecuatii diferentiale sau integro-diferentiale care, dupa caz pot fi rezolvate fie prin metodele clasice (v. Ecuatiile fizicii-matematice), fie prin aplicarea unor operatori de transformare -cum ar fi transformata Laplace (v.§ 9.1.5) care este justificata aici -cand perturbatia se considera de forma (TR1)- deoarece, in acest caz, in circuite apar functii de discontinuitate si derivatele acestora si se cauta solutia unor ecuatii diferentiale in aceste conditii.

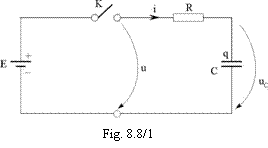
Spre exemplificare se va considera studiul regimului tranzitoriu de "incarcare" a unui condensator de la o sursa de curent continuu, cu t.e.m. E, prin inchiderea brusca a intreruptorului K (fig. 8.8/1). Condensatorul electric cu capacitatea C (considerat ideal) este in serie cu un rezistor cu rezistenta electrica R.

Presupunandu-se ca inchiderea intreruptorului K este foarte rapida si are loc la t=0, rezulta ca tensiunea u ce se aplica laturii R, C este data de functia:

(TR 2) sau u=Eh,

adica de treapta unitate Heaviside h -definita prin expresia (TR1)- multiplicata cu E. Dupa inchiderea brusca a intrerupatorului K, urmeaza regimul tranzitoriu de incarcare a condensatorului, in care sarcina electrica pe armaturile condensatorului (q), curentul electric din circuit (i) si tensiunea la bornele condensatorului (u_c) sunt functii de timp: q(t), i(t) si u_c(t); scopul analizei acestui regim tranzitoriu (de incarcare a condensatorului electric) este tocmai acela de a determina aceste functii de timp.

Modelul original (initial), al acestui regim tranzitoriu (cu sensurile de referinta indicate ca in figura 8.8/1) este (dupa cum se stie din subcap. 8.4):

,

si i=dq/dt=,

, (TR 3)

etc.

Ultima ecuatie, tinandu-se seama de expresia (TR 2) a lui u, se mai poate scrie si in forma:

,

sau -impartindu-se cu si notandu-se cu τ=RC- in forma:

sau . (TR 4)

Termenul RC are dimensiunea de timp, se noteaza cu τ si se numeste constanta de timp a circuitului R, C serie. Intr-adevar dimensional rezulta:

.

Semnificatia fizica, dar si geometrica (referitoare la reprezentarea marimilor q, u, u_R, . in raport cu timpul), va fi aratata ceva mai incolo.

Pentru t>0 solutia ecuatiei diferentiale (TR 4), care reprezinta problema lui Cauchy cu conditii initiale, este de forma:

q=q_l+q_p (TR 5)

unde q_l este "solutia libera", adica solutia ecuatiei omogene:

, (TR 6)

care se otine separandu-se variabilele si integrandu-se membru cu membru:

, (TR 7)

unde q_o este constanta de integrare, o constanta arbitrara determinata prin conditia initiala.

Termenul de q_p, din solutia (TR 5) a problemei Cauchy (TR 4), reprezinta o solutie particulara a ecuatiei neomogene; o astfel de solutie particulara este sarcina electrica de pe armaturile condensatorului in regimul permanent care urmeaza dupa regimul tranzitoriu de incarcare, cand condensatorul ajunge la sarcina maxima posibila q_p=CE (determinata de t.e.m. E).

Atunci solutia (TR 5), in care se inlocuieste q_l cu expresia ei (TR 7) si q_p cu CE, devine:

, (TR 8)

care, in conditiile initiale -la t=0- face q(t=0)=0 (deoarece condensatorul este neincarcat) si atunci (TR 8) devine:

,

ceea ce permite determinarea constantei de integrare: q_o CE, astfel ca expresia definitiva a solutiei (TR 8) este:

sau , (TR 9)

unde Q este sarcina electrica a condensatorului in noul regim permanent.

Reprezentarea grafica a solutiei (TR 9) este data in figura 8.8/2a; asadar condensatorul se incarca exponential, viteza de incarcare depinzand de constanta de timp τ (aici τ=RC).

Aceasta semnificatie a lui τ este dovedita, concret, prin urmatoarele:

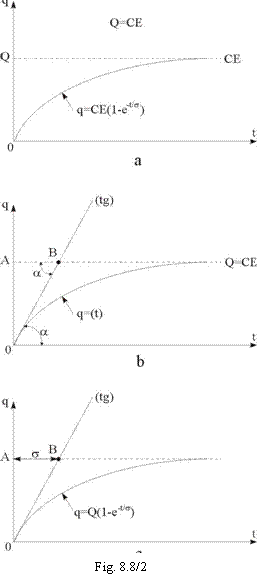- daca la exponentiala solutiei q(t) se duce, intr-un punct oarecare (de exemplu, chiar in originea O), tangenta geometrica, (tg) in figura 8.8/2b, atunci -din triunghiul dreptunghic OAB- rezulta:

(TR 10),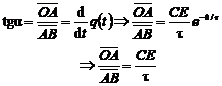

conform interpretarii pe care o are derivata unei functii (ca fiind tangenta trigonometrica a tangentei geometrice la curba ce reprezinta functia, in punctul considerat - aici originea O, unde t=0). Deoarece segmentul este Q=CE (=Q=CE) rezulta din ultima egalitate (TR 10) ca:

(TR 11) ,

adica τ (constanta de timp) este egala cu subtangenta la curba q(t) in punctul considerat (in exemplul din figura 8.8/2b este subtangenta in punctul O, in origine, asa cum se arata in figura 8.8/2c);

- daca se considera t=3τ si se calculeaza valoarea sarcinii electrice a condensatorului in regim tranzitoriu (deci la un moment egal cu trei constante de timp dupa inceperea acestui regim) se constata:

,

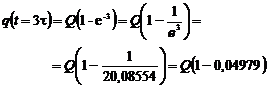adica, rotunjind valoarea lui e^-3 la 0,05, rezulta:

q(t=3τ)=0,95Q,

ceea ce inseamna ca dupa numai trei constante de timp, in regimul tranzitoriu se ajunge la 95% din valoarea finala (atinsa teoretic la un timp infinit) a noului regim permanent. In multe aplicatii din Electronica se considera ca suficienta atingerea valorii de 90% din cea finala; in aceasta situatie timpul in care se ajunge la acest nivel (numit adesea timp de stabilire) este:

si .

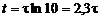Practic, se considera ca dupa 2,3τ la 3τ regimul tranzitoriu a luat sfarsit.

Celelalte marimi electrice ale circuitului R, C (fig.8.8/1), in regim tranzitoriu se determina direct din q(t) cu relatiile (TR 3); astfel:

- intensitatea curentului electric i(t) este:

(TR 12)              ,

adica in momentul inchiderii bruste a contactului K din figura 8.8/1 (la t=0), in circuit apare un "soc" de curent , dupa care curentul scade exponential, cu o subtangenta τ, pana la zero (t i=0);

- tensiunea la bornele condensatorului electric u_c(t) este:

, (TR 13)

ceea ce inseamna ca ea creste de la u_c=0 (pentru t=0) la u_c=E, teoretic la infinit (t).

O interpretare energetica are rolul de a dovedi faptul ca regimul tranzitoriu, de exemplu pentru circuitul R, C din figura 8.8/1, este impus de necesitatea transferarii energiei electrice necesare producerii campului electric in dielectricul condensatorului. Astfel, energia disipata ireversibil in caldura in intervalul de timp de la 0 la t este (conform legii transformarii de energie in conductori):

Energia produsa de sursa in acelasi interval de timp este:

.

Se constata ca W_EW_R, fiind mai mare. Rezulta ca nu toata energia produsa de sursa a fost transformata in caldura. Diferenta:

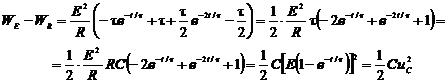
reprezinta energia electrica acumulata in campul electric al condensatorului cu capacitatea electrica C, corespunzator valorii u_c a tensiuni la bornele sale.

Considerandu-se din nou schema din figura 8.8/1, daca se ia R=0 atunci va rezulta u(t)=Eh si prin urmare:

Q=Cu=CEh=Qh, (TR 14)

pentru cazul cand q(t<0)=0. Asadar condensatorul se incarca brusc cu sarcina Q=CE, ceea ce inseamna ca q(t) este de forma treptei Heaviside, cu saltul Q in origine. Se pune acum problema determinarii curentului cu care se incarca acest condensator (cand R=0); din relatia (TR 14) va rezulta:

(TR 15)

Asadar, pentru t=0 curentul este i=0, iar pentru t>0 curentul este de asemenea i=0 si deoarece in origine h(t) nu este derivabila se poate trage concluzia ca i este zero peste tot, cu exceptia originii, unde ia o valoare infinita. Acest raspuns nu este insa satisfacator, deoarece daca se inlocuieste E cu 2E, atunci sarcina electrica devine 2Q, iar saltul in origine a lui q(t) este acum 2Q. Se pune, firesc, intrebarea: in acest caz (in care in loc de E s-a luat 2E) curentul este "infinit" in origine exact ca in cazul precedent? (s-ar putea, in mod naiv, sa se intrebe "cat de infinit" este in acest caz curentul i ?!). Iata, deci, ca este necesar sa se generalizeze notiunea de derivata astfel incat o functie cu salt sa fie derivabila in punctul de salt, iar derivata sa exprime si marimea saltului. Aceasta generalizare o realizeaza teoria distributiilor (ale carei notiuni de baza sunt prezentate in paragraful 9.1.5).

Pe baza acestor notiuni, in cazul din figura 8.8/1 unde sarcina electrica a condensatorului cu capacitatea C (pus brusc sub tensiunea constanta E la t=0), daca la t<0 el este descarcat, are expresia:

Q=ECh(t)=Qh(t),

iar curentul prin condensator este:

(TR 16)               i=Dq=QDh=Qδ,

unde D este operatorul pentru derivarea distributiilor (v.§ 9.1.5) si δ reprezinta functia impuls a lui Dirac. Expresia (TR 16) arata ca intensitatea curentului i depinde de valoarea saltului Q.

Desi distributia Dirac, δ(t), nu este de tip functie, se poate calcula cu functii care sunt siruri reprezentative Dirac si care converg slab catre distributia Dirac. Convergenta slaba face metoda inutilizabila in calculul numeric. Pentru exemplul condensatorului, la care prin expresia (TR 12) s-a determinat:

daca se considera , atunci si se obtine sirul reprezentativ Dirac:

(TR 17)                      .

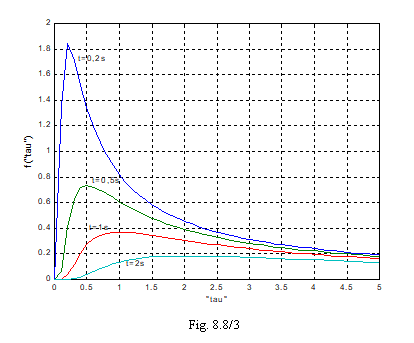Reprezentarea grafica a sirului (TR 17) e^-t/τ/τ=f(τ), pentru cateva valori ale timpului, obtinuta printr-un program de rutina MATLAB, arata asa ca in figura 8.8/3 (considerandu-se t=const.0, pentru ca la t=0 sirul este 1/τ), si evidentiaza clar ce se intampla cand t0. Astfel, la t=0,2s (un timp destul de departe de t=0) se remarca trecerea la impulsul Dirac exponential.

Pentru R foarte mic rezulta i(+0)=E/R foarte mare, iar τ devine foarte mic (deci exponentiala tinde rapid catre zero, fiind un "impuls exponential"). Acest exemplu este intuitiv, dar nu este riguros deoarece solutia s-a obtinut pentru R0 (singurul caz posibil practic, deoarece R=0 este un caz ideal, neexistand in realitate conductori perfecti pentru conectarea condensatorului la o sursa, care -si ea- nu poate fi ideala, adica cu rezistenta interna r=0). Dealtfel, R=0τ=0 pentru care sirul (TR 17) este nedeterminat.

Se vor considera, in continuare, alte doua cazuri semnificative pentru aplicatiile practice.

Rezistor in serie cu o bobina ideala (fig.8.8/4). Daca se conecteaza brusc (prin inchiderea rapida a intrerupatorului K) o sursa electrica cu t.e.m. constanta E la bornele unei laturi R, L serie (fig.8.8/4), tensiunea la borne va fi:

u=Eh(t)=Eh

astfel ca modelul ce descrie regimul tranzitoriu care se produce cand la t=0 se inchide K este:

(TR 18)                Ri+Ldi/dt=Eh.

Impartindu-se cu L, relatia (TR 18) devine:

(TR 19)                             sau ,

in care s-a facut inlocuirea L/R=τ. Acest termen, L/R, are dimensiunea timp si este denumit constanta de timp (τ) a circuitului R, L serie. Intr-adevar, dimensional:

.

Ecuatia diferentiala (TR 19) are solutia:

i=i_l+i_pt>0,                 (TR 20)

unde i_l este solutia "libera" (a ecuatiei omogene) si i_p este o solutie particulara a ecuatiei neomogene (TR 19), care reprezinta o problema Cauchy cu conditii initiale.

Luandu-se ecuatia omogena i/t+di/dt=0 si separand-se variabilele, adica scriindu-se in forma di/i dt/t, rezulta, prin integrare: lni=-t/τ+lnI_o, unde I_o este constanta de integrare (o constanta arbitrara ce se va determina din conditiile initiale). Atunci solutia libera a curentului este:

I_l=I_oe^-t/τ.

O solutie particulara a curentului, i_p, este aceea din regimul permanent la care se va ajunge atunci cand o bobina ideala (adica avand numai parametrul L, cu R=0 si C=0) este conectata printr-un rezistor la o sursa ideala de curent continuu (cu t.e.m. E si rezistenta interna r=0) si care este: i_p=E/R. Atunci solutia (TR 20) devine:

i=I_oe^-t/τ+E/R, (TR 21)

care in conditiile initiale -cand t=0i(t=0)=0, deoarece miezul bobinei initial nu este magnetizat- devine:

0=I_oe^-t/τ+E/R I_o=-E/R.

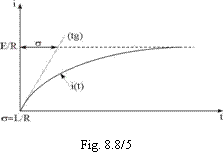Atunci expresia definitiva a intensitatii curentului electric, i(t), din circuitul unei bobine ideale conectata brusc la o sursa de curent continuu printr-un rezistor este:

, (TR 22)

al carui grafic i(t) este aratat in figura 8.8/5.

Tensiunea la bornele bobinei din figura 8.8/4, u_L(t), din regimul tranzitoriu se determina imediat, fiind cunoscuta expresia (TR22) a curentului i(t) din latura R, L serie:

(TR 23)

Pentru R foarte mic rezulta u_L(+0) = E, cea mai mare tensiune posibila in regim tranzitoriu a tensiunii la bornele bobinei. La limita, cand R = 0 (cazul bobinei ideale), prin ridicarea nedeterminarii din formula (TR 22) rezulta:

care creste liniar indefinit.

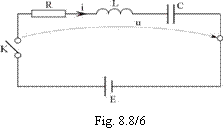
Latura R, L, C serie conectata brusc la o sursa de curent continuu (fig. 8.8/6). Daca se aplica brusc (prin inchiderea rapida a intrerupatorului K) o t.e.m continua E, deci o tensiune la borne in forma unei functii treapta: u(t) = Eh(t) T u(t<0) = 0, atunci va urma un regim tranzitoriu caracterizat de un curent i = i(t) cu i(t<0) = 0 si avand modelul (v. subcap. 8.4):

(TR 24)

care reprezinta o ecuatie integrodiferentiala cu conditii initiale, tipica pentru descrierea sistemelor fizice cu un singur grad de libertate.

Pentru a se exemplifica si modalitatea de utilizare a calculului operational bazat pe transformata Laplace in studiul regimului tranzitoriu al circuitelor electrice, se va determina expresia curentului i(t) -ca solutie a ecuatiei (TR 24)- aplicandu-se acestei ecuatii, in fiecare membru, transformata Laplace (v. § 9.1.4). Se va obtine (considerandu-se conditiile initiale nule):

(TR 25) LL

de unde rezulta transformata Laplace a curentului I(s):

(TR 26) .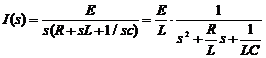

introducandu-se notatiile:

R/L = 2αsi1/LC = ω₀² ,

unde α reprezinta atenuarea circuitului si ω₀ - pulsatia oscilatiilor libere ale circuitului L, C (v. § 2), expresia transformatei Laplace a curentului devine:

(TR 27)

care este de forma unei fractii rationale P(s)/Q(s) cu:

P(s) s 1 si Q(s) s s² + 2as w₀²

avand, deci, originalul (ca functie de timp) data de teorema de dezvoltare a lui Heaviside (v. § 9.1.4) si anume:

L ^-1 ,

unde Q'(s) = dQ(s)/ds -in cazul expresiei (TR 27) Q'(s) = 2s + 2α- iar s_k(k = 1,2,,n) sunt radacinile simple ale ecuatiei Q(s) = 0, care pentru cazul relatiei (TR 27) sunt:

s² + 2αs + ω₀² = 0 T s_1,2 = a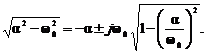

Atunci expresia curentului i(t), din regimul tranzitoriu al circuitului R, L, C serie (v. fig. 8.8/6), este:

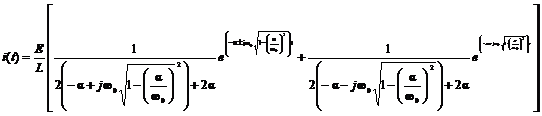
sau, in definitiv:

(TR 28)