
|
|
|
FUNCTIONAREA MEMORIILOR ASOCIATIVE BIDIRECTIONALE
m
1. Stabilirea ponderilor
Consideram o memorie asociativa bidirectionala (MAB) compusa din straturile (campurile) Fx si Fy. Fiecare neuron poate avea si o legatura spre el insusi (vezi Figura 1), care corespunde unei bucle in graful ce descrie topologia retelei.
Admitem ca multimea de instruire este formata din perechile
![]()
unde xi e Bn, yi e Bm. Prin Bn am notat fie cubul boolean n-dimensional n, fie cubul n.
Spre deosebire de cele mai multe retele, ponderile MAB nu se determina printr-un mecanism iterativ de instruire. Ca si in cazul deja considerat al Asociatorului liniar, aceste ponderi se calculeaza o singura data si raman neschimbate pe toata durata functionarii retelei.
Desi vectorii x1, x2.. x. nu sunt, in general, ortonormati, putem alege
matricea W a ponderilor ca fiind data de formula utilizata pentru asociator. Vom considera ca W este suma matricelor de corelatie
![]()
|
|
Figura 1. Reprezentarea unei MAS. Vom avea, deci
|
|
W este o matrice (m x n) si da ponderile conexiunilor de la stratul Fy spre stratul Fx. Linia J a matricei contine ponderile conexiunilor neuronului J din campul de iesire. Ponderile conexiunilor de la campul Fx la F2 sunt date de matricea WT. Asadar, coloana I a matricei W contine ponderile conexiunilor neuronului I din campul Fx. Matricea W codifica primele p perechi de forme. Pentru a codifica o noua pereche (xk, yk) se calculeaza matricea de corelatie
![]()
si se aduna wk la matricea W.
Daca xi e n , matricea W se poate defini in mod alternativ, ca fiind
|
|
|
|
|
unde cu |
am notat suma booleana.
Valorile -1 si 1 sunt mai potrivite decat 0 si 1 pentru codificarea starilor, deci primul pas este de a converti in .
2. Dinamica MAB-urilor
Dupa stabilirea matricei ponderilor, o memorie asociativa bidirectionala poate fi folosita pentru a regasi o anumita informatie atunci cand se prezinta retelei o anumita informatie-cheie. De exemplu, informatia regasita poate fi numarul de telefon al unei persoane, iar informatia-cheie asociata poate fi numele si adresa acelei persoane. Daca informatia necesara este doar partial cunoscuta (se stie, de exemplu, doar numele unei persoane) sau daca ea este distorsionata (numele sau adresa sunt inexacte), reteaua este capabila sa furnizeze, totusi, numarul de telefon corect, completand sau restabilind si informatia-cheie.
2.1. Dinamica neuronilor individuali
Vom descrie, acum, o MAB discreta aditiva. in aceasta memorie, timpul are valori discrete, iar functia neuronala este o functie prag.
Fie x(t) vectorul format din starile neuronilor stratului Fx la timpul t. Componentele acestui vector pot fi sau . xff) reprezinta starea neuronului i din campul Fx la timpul t. Notam cu S(- activarea neuronului i.
Intrarile neuronului i din campul Fx sunt date de iesirile Vj(t), j = 1, 2. m,
ale neuronilor din stratul Fy. Se poate scrie deci activarea Sf sub forma
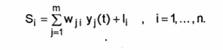
Termenul i, corespunde unei intrari externe a neuronului I.
Activarea R,a neuronului / din stratul Fy se calculeaza folosind iesirile
![]()
ale neuronilor din stratul Fx. La momentul t, aceasta activare este
![]()
Termenul J. corespunde unei eventuale intrari din exterior a neuronului;'. Daca starile neuronilor sunt 0 si 1, atunci starea neuronului-i la momentul (t+1) va fi Xj(t+1), unde
|
|
|
|
Starea neuronului; din campul Fy la momentul (t+1) este yj(t+1), unde
|
|
|
|
|
|
|
|
Am notat cu u,- si v, pragurile celor doi neuroni. in cazul neuronilor bipolari (cu starile -1 si +1), expresiile de mai sus se vor modifica punand
|
|
si, respectiv
![]()
I ^ *l
Putem absorbi, pragul in matricea ponderilor procedand in modul uzual, adica adaugand vectorilor x(t) si y(t) o ultima componenta egala cu 1.
2.2. Modelul de activare
Pentru schimbarea starilor, putem folosi fie un model sincron, fie unul asincron de activare. intr-un model sincron, neuronii unui camp se actualizeaza simultan.
intr-un model de activare asincron, la fiecare moment se actualizeaza o submultime a neuronilor din campurile Fx sau Fy. Daca activarea neuronilor este aleatoare, atunci comportarea acestora se asimileaza cu un proces aleator scalar iar functionarea retelei se poate descrie ca un proces aleator vectorial.
Daca, la un moment t, se schimba starea unui singur neuron, atunci avem de-a face cu un proces asincron simplu.
Se poate defini, astfel, in mod abstract, o memorie asociativa bidirectio≠nala ca fiind un sistem S cu sapte componente: S = (Fx, Fy, W, I, J, U, V), unde Fx sj FY au semnificatiile cunoscute. I si J sunt vectori coloana ce desemneaza intrarile din mediu. U si V sunt vectori coloana reprezentand pragurile neuronilor din campul Fx si respectiv F (vectorii I si U sunt n-dimensionali iar vectorii J si V au cate m componente).
Functionarea MAB-urilor. Exemple
Vom considera cateva exemple de functionare a memoriilor asociative bidirectionale. Aceste exemple incearca sa puna in evidenta diferitele situatii ce pot sa apara in legatura cu regasirea unei forme memorate.
Exemplul 1.
Consideram o memorie asociativa bidirectionala bipolara avand n=8 neuroni pe stratul de intrare Fx si m=5 neuroni pe campul Fy. Consideram, in plus, toate pragurile egale cu zero: Uj = v, = 0 ,Vi, j.
Fie o multime de instruire formata din vectorii (x1, y1) si (x2, y2), unde
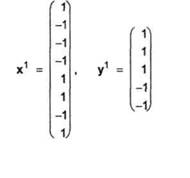
|
|
|
Fie vectorul de intrare |
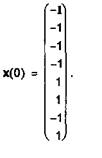
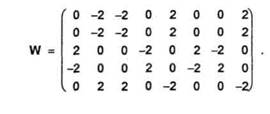
Dorim sa construim o retea capabila sa recunoasca faptul ca x(0) este o versiune distorsionata a lui x1. Matricea ponderilor retelei este
![]()
Se obtine
Folosind un model de activare sincron, activarile neuronilor din stratul F. sunt:
|
|
|
|
Luam, de exemplu,
|
|
si calculam starea y(1) a neuronilor din Fy la momentul t = 1:
|
|
Obtinem, astfel

Cu vectorul y1, calculam activarile neuronilor din stratul Fx :
![]()
Gasim valorile
![]()
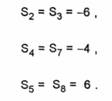
Vectorul de stare pentru neuronii din Fx la momentul t = 1 va fi
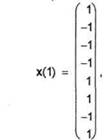
care este chiar x1. Propagand aceasta stare
inainte, spre campul Fy , obtinem si deci, avem![]()
![]()
Rezulta ca reteaua s-a stabilizat de la prima iteratie, realizandu-se echilibrul bidirectional. S-a obtinut astfel ca x(0) produce raspunsul y1 sau, echivalent, ca x(0) este o versiune distorsionata a lui x1.
Exemplul 2.
Consideram reteaua si multimea de instruire din exemplul anterior si dorim sa vedem cum se comporta aceasta retea daca vectorul de intrare x(0) difera mult fata de x1 si x2.
Alegem, de exemplu,
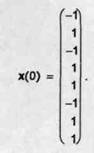
Gasim activarile
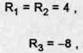
![]()
![]()
Rezulta ca
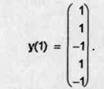
Activarile stratului Fx produse de y(1) sunt:
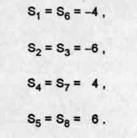
Vectorul de stare asociat este
|
|
si el produce, in Fy, activarile
|
|
|
|
Vectorul de stare generat de aceste activari este
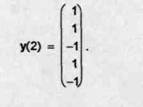
Se observa ca
![]()
Rezulta ca, in continuare, vom avea
![]()
si, deci
![]()
adica reteaua s-a stabilizat.
Este interesant de observat ca solutia gasita indica un punct de echilibru (x(1). yC)) care nu coincide cu nici una dintre perechile de instruire. Astfel, distanta Hamming intre x(1) si x1 este 3, iar cea dintre y(1) si y1 este 2.
4. Algoritmul MAB
Considerentele anterioare, precum si exemplele precedente ne permit sa formulam un algoritm pentru memorarea si regasirea informatiei intr-o memorie asociativa bidirectionala. Vom lua cel mai general dintre modelele considerate, adica modelul
![]()
Algoritmul de regasire corespunzator acestui model este prezentat in continuare.
ALGORITMUL DE MEMORARE Sl DE REGASIRE A INFORMATIEI IN MEMORIILE ASOCIATIVE BIDIRECTIONALE
P1. Se construieste matricea W a ponderilor, folosind o multime de instruire formata din perechile de asociatii
![]()

w = £yV
i=1
P2. Se pune t := 0.
PSe initializeaza starile neuronilor din campul Fy folosind un vector arbitrar y(0).
P4. Se prezinta retelei un vector x = x(0) (fortand la x(0) iesirile neuronilor din campul Fx). Se urmareste regasirea vectorului x' din multimea de instruire, cel mai apropiat de x(0) in sensul distantei Hamming.
P5.se propaga informatia de la campul Fx spre stratul Fy si se actualizeaza starea neuronilor din Fy. Prin urmare, acest pas presupune urmatoarele :
(l)alegerea strategiei de actualizare, sincrona sau asincrona ; (ii) calcularea vectorului R al activarilor,
![]()
(iii) calcularea vectorului de stare y(t+1) al neuronilor din Fy comparand componentele lui R cu pragurile corespunzatoare; se utilizeaza regula de evolutie
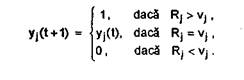
P6. Informatia stratului Fy se propaga inapoi spre campul Fx. Se actualizeaza neuronii campului Fy. Aceasta implica faptul ca
(0se alege o strategie de actualizare ;
(ii) se calculeaza vectorul S al activarilor,
![]()
|
Observatie: Pentru neuronii bipolari, se pune |
|
si, respectiv |
(iii) se calculeaza vectorul de stare x(t+1) al neuronilor din campul FK folosind regula
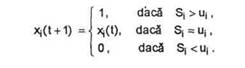
![]()
![]()
p7. Se pune t := t+1. Se repeta pasii P5 si P6 pana cand starea nici unui neuron .jSrt'-' nu se mai schimba.
in acest algoritm se prezinta retelei (memoriei asociative) un vector x(0) care contine o informatie despre vectorul x' dorit, dar nu stim nimic despre vectorul y asociat. Se spera ca, la echilibru, sa obtinem o stare (x, y), unde x este vectorul x1 din multimea de instruire, care este cel mai apropiat de x(0).
Algoritmul precedent functioneaza bine daca reteaua nu este supraincarcata (multimea de instruire nu este prea mare). in cazul supraincarcarii, apare un fenomen de interferenta datorata faptului ca formele de invatare sunt prea apropiate. Interactiunea dintre aceste forme poate genera stari de echilibru false, analoage cu punctele de minim local ale unei functii criteriu.
Putem considera, acum, si un model simplificat de memorie asociativa bidirectionala, in care nu exista intrari din mediu. Acest model este descris de sistemul
![]()
Vectorii de activare se vor calcula cu relatiile
![]()
si, respectiv![]()
Algoritmul general prezentat mai sus nu mai necesita alte modificari.