Regimul deformant

_{Regimul deformant}

1. Bazele analizei armonice

Abaterile de la forma ideala pot fi caracterizate in baza analizei armonice, prin punerea in evidenta a oscilatiilor armonice cu perioade submultipli intregi ai perioadei fundamentale, evidentiata ca perioada a undei reale. Evidentierea corecta a periodicitatii undei nesinusoidale are o deosebita importanta, pentru ca altfel se pot pierde interarmonici si subarmonici [45].

a) Dezvoltarea Fourier pentru functii cunoscute analitic

Este cunoscut faptul ca o functie y(x), periodica, cu perioada T=2l, care satisface conditiile lui Dirichlet in intervalul (0, 2l) poate fi dezvoltata in serie trigonometrica Fourier sub forma

, (2.52)

in care coeficientii a_N si b_N sunt dati de relatiile:

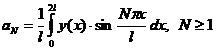; (2.53)

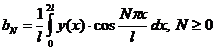, (2.54)

a caror utilizare necesita cunoasterea expresiei analitice a functiei y(x).

Dezvoltarea Fourier conform relatiei (2.52) converge uniform spre y(x), putand fi utilizata pentru calculul aproximativ al valorilor functiei y(x) in intervalul considerat si pentru aprecierea regimului deformant. Functiile si , multiplicand functia y(x), pot fi denumite functii de modulatie; prin faptul ca aceste functii permit extragerea marimilor caracteristice unei anumite armonici din semnalul y(x), aceste functii ar putea fi denumite si functii de filtrare [52].

b) Dezvoltarea Fourier pentru functii esantionate

In tehnica, utilitatea analizei armonice este pentru functii, care nu sunt cunoscute analitic, ci numai grafic sau tabelar. Prelucrarea numerica a semnalelor si conversia analog-digitala au condus la esantionarea formelor de unda, de tensiune sau de curent, conform reprezentarii din figura 2.17, in care esantioanele Y_k corespund valorilor functiei de analizat y(t) la momentele t_k. Se observa ca perioada T este divizata in 2p parti egale, astfel incat momentele t_k sunt date de relatia

. (2.55)

Analiza armonica a undelor reale de tensiune sau curent, obtinute pe cale experimentala, prin oscilografiere sau inregistrare, presupune asadar, mai intai, identificarea perioadei fundamentale T si impartirea acesteia in 2p parti egale, deci p parti pe o semiperioada (fig. 2.17).

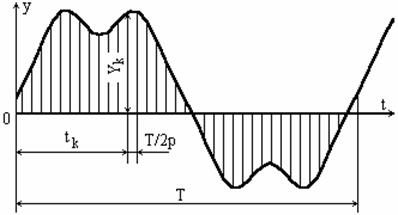
Fig. 2.17. Divizarea perioadei unei unde periodice nesinusoidale, in vederea analizei armonice.

Desigur, numarul de diviziuni este limitat inferior de ordinul maxim al armonicilor care se impun a fi identificate. Aici se impune precizarea ca fiecare armonica este o marime fazoriala, pentru care se impun a fi determinate atat amplitudinea, cat si faza, deci doua marimi fizice pentru fiecare armonica. Urmatoarea teorema, care poate fi considerata ca o precizare a aplicarii teoremei lui Nyquist la analiza armonica, cu utilizarea transformatei Fourier discrete, se impune a fi enuntata de la bun inceput:

pe baza a 2p esantioane pe o perioada a fundamentalei, se pot determina corect componenta continua, daca exista, si (p-1) armonici, identificate fiecare prin amplitudine si faza.

Limitarea superioara a numarului de diviziuni este datorata posibilitatilor de 'citire' a valorilor functiei sau functiilor analizate. Astfel, daca se cunosc frecventa maxima de esantionare f_eM si numarul de marimi (canale) esantionate N_m, numarul maxim de esantioane N_eT pe o perioada (nominala) a fundamentalei acestora este dat de relatia:

, (2.55)

in care f_n = 1/T este frecventa nominala a undelor esantionate. Deoarece nu se recomanda lucrul sistemelor de achizitie la frecventa maxima de esantionare, numarul real de esantioane pentru o marime de analizat, pe o perioada a fundamentalei, va fi mai mic decat cel determinat cu relatia (2.55).

Daca se considera ca se cunosc 2p esantioane ale unei unde de analizat, fie aceasta de tensiune sau de curent (fig. 2.17), notate prin

Y_k, k I , (2.56)

expresiile coeficientilor Fourier se calculeaza corect cu relatiile [52]:

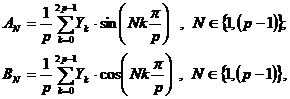(2.57)

iar componenta continua se calculeaza cu relatia

, (2.58)

in care N este ordinul armonicilor, cu valori in domeniul precizat la relatiile (2.57).

Dezvoltarea Fourier a undei cautate y(t) se prezinta mai intai sub forma:

(2.59)

sau prin expresia mai condensata

(2.60)

in care amplitudinea si faza unei armonici se determina, respectiv, cu relatiile

(2.61)

(2.62)

iar este pulsatia corespunzatoare fundamentalei.

In ceea ce priveste faza φ_N a armonicii de rang N, determinarea corecta trebuie sa tina seama de urmatoarele aspecte:

definirea fazei este continuta in relatia (2.60);

se determina faze φ_N ≥ 0, situate in intervalul [0, 2p

calcularea fazei φ_N are sens numai pentru cazul Y_N 0 (A_N si B_N nu pot fi deci concomitent nule);

in cadrul programelor pe calculator (LabVIEW, C, Pascal), functia arctg(x) este cu valori numai in intervalul .

Determinarea corecta a fazelor este tot atat de importanta ca si a amplitudinilor. In consecinta, la calcularea fazelor φ_N se impune luarea in considerare a semnelor coeficientilor A_N si B_N, in vederea plasarii fazelor in cadranul corect. In continuare, se propune urmatorul algoritm de identificare a fazelor, algoritm verificat printr-un program realizat [42]:

- daca A_N <0,

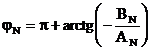; (2.63)

- daca A_N =0 (deci B_N 0),

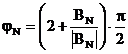; (2.64)

- daca A_N >0,

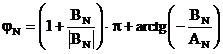, (2.65)

cu cazul particular φ_N = 0, daca in plus B_N =0. In relatiile (2.64) si (2.65), notatia semnifica modulul (valoarea absoluta) valorii B_N.

De remarcat ca identificarea completa a unei armonici, de ordin N dat, se face fie prin perechea de coeficienti Fourier (A_N, B_N), fie prin perechea amplitudine - faza (Y_N, j_N

2. Numarul de diviziuni si erori de calcul

Numarul de diviziuni (2p) este important, in primul rand, pentru ordinul maxim al armonicii care se poate determina corect si care este

, (2.66)

contrar opiniei, redata si prin unele teoreme si relatii, ca se pot identifica p armonici. Un prim argument il constituie observatia ca din cele (2p) conditii (p perechi de abscise-ordonate) initiale se determina componenta continua si 2(p-1) coeficienti, pentru (p-1) armonici, deci in total (2p-1) date, in timp ce pentru p armonici ar trebui calculate (2p+1) date, pentru care deci conditiile initiale sunt insuficiente. Relatia (2.66) subliniaza ideea reconstituirii undei din (p-1) armonici, corect determinabile si din componenta continua, atunci cand aceasta exista.

In al doilea rand, este important de stiut in ce masura numarul de diviziuni (2p) influenteaza precizia de identificare a fiecarei armonici si deci a undei rezultante. Argumentarea analitica, intelesul si exemplificarea prin calcule concrete a acestei afirmatii se realizeaza in cele ce urmeaza.

Pentru aceasta, se considera armonica de ordinul N sub forma generala

, (2.67)

asa cum apare in scrierea condensata a dezvoltarii Fourier din relatia (2.60), pentru care sunt cunoscute 2p esantioane pe intervalul xI[0, 2p), avand valorile

, ; (2.68)

ultima notatie indica faptul ca numarul natural k ia valori de la 1 la 2p (se observa ca prima valoare calculata corespunde abscisei x=0).

Calculul coeficientilor Fourier pentru armonica considerata se face cu relatiile (2.57), (2.58) cu deosebirea ca indicele de insumare se ia (ca in unele materiale de specialitate) si nu in domeniul , cum apare in relatiile referite.

Formele initiale ale relatiilor de calcul sunt, in acest caz, urmatoarele:

; (2.69)

, (2.70)

care prin transformari elementare si utilizarea formulelor pentru sume de forma

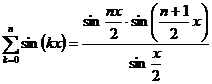; (2.71)

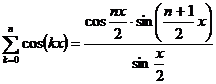, (2.72)

conduc la expresiile [52]:

; (2.73)

. (2.74)

De remarcat, in primul rand, invarianta valorii amplitudinii Y_N, care - rezultand ca in relatia (2.61) - nu depinde de domeniul indicelui de insumare k, daca acesta ia (2p) valori distincte. Se poate formula astfel o teorema a independentei valorilor amplitudinilor Y_N de limitele de insumare, daca se acopera acelasi interval de insumare, corespunzator unei perioade a fundamentalei.

In al doilea rand, se observa ca desi prin modul de generare a esantioanelor Y_Nk (rel. 2.68) se descrie acelasi sir de valori ca in relatiile (2.57) si (2.58), faza calculata este mai mare decat faza j_N cu marimea

, (2.75)

care reprezinta o eroare de calcul a fazei, dependenta de numarul p, fiind invers proportionala cu acesta si de rangul N al armonicii, in mod proportional [14]. Explicatia aparitiei acestei erori de faza rezida in sirul de valori ale functiilor de modulatie si , distinct in cazul in care fata de .

In concluzie, daca se lucreaza cu relatiile (2.57) si (2.58) nu se face eroare de faza la identificarea armonicilor, iar daca se utilizeaza relatiile

; (2.76)

, (2.77)

atunci se impune corectia fazelor cu marimea data de relatia (2.75), faza corecta fiind

, (2.78)

in care j_N reprezinta faza determinata din coeficientii A_N si B_N, calculati cu relatiile (2.76) si (2.77), respectiv.

Influenta erorii de faza este pusa in evidenta in figura 2.18 pentru o marime pulsatorie, nesinusoidala, de analizat YA, de compozitie armonica cunoscuta; in calcule s-au introdus insa esantioanele determinate pentru un numar de diviziuni (2p) suficient de mare, pentru ca toate armonicile sa fie identificabile. Analiza armonica, bazata pe relatii de forma (2.76), (2.77) si reconstituirea undei Y din armonicile identificate, conduce la o decalare in urma a undei reconstituite Y in raport cu cea analizata YA. S-a verificat si s-a pus astfel in evidenta faptul ca, prin corectia fazelor armonicilor dupa relatia (2.78), unda reconstituita se suprapune peste cea analizata.

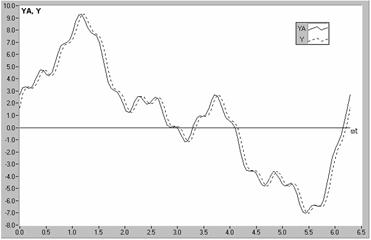
Fig. 2.18. Formele de unda ale functiei reale, analizate YA si celei reconstituite Y,

prin transformata Fourier discreta, daca indicele de insumare k I

Din punct de vedere practic 22 , se considera suficienta limitarea analizei la primele 40 de armonici, deci N_max= 40. Alte standarde prevad rangul maxim al armonicii de luat in calcule din domeniul N_max I 20, 50

In final, se impune infirmarea ipotezei conform careia numarul de esantioane pe perioada mareste precizia de identificare a armonicilor. De fapt, numarul de esantioane pe o perioada determina numarul de armonici identificabile si prin aceasta - precizia de identificare a functiei periodice, dar nu influenteaza precizia de determinare a coeficientilor Fourier, pentru armonicile identificabile.

3. Armonica de rang p

Conform teoremei esantionarii a lui Shannon, esantionarea unui semnal periodic, nesinusoidal trebuie sa se faca cu o frecventa f_e de cel putin doua ori mai mare decat frecventa f_max a armonicii de rang maxim, care urmeaza sa fie evidentiata in urma analizei spectrale a acestui semnal:

. (2.79)

Frecventa reprezentand jumatatea frecventei de esantionare (f_e/2) este denumita frecventa Nyquist 52 , aceasta avand rangul p.

Introducand in relatia (2.79) frecventa maxima in raport cu frecventa fundamentala

(2.80)

se obtine o forma a teoremei lui Shannon, care indica rangul maxim al armonicii determinabile, pentru o unda esantionata

(2.81)

Semnul egal, permis de relatia (2.81), este insa discutabil prin prisma numarului de conditii distincte, existente. Astfel, asa cum s-a mai subliniat la paragraful 2, cele (2p) esantioane, reprezentand de fapt tot atatea corespondente abscise-ordonate, se constituie in (2p) conditii initiale, matematic disponibile. Daca s-ar admite ca se pot determina p armonici, deci (2p) marimi (amplitudinea si faza pentru fiecare armonica), plus componenta continua, inseamna ca s-ar putea determina (2p+1) marimi, ceea ce este absurd, pentru-ca se dispune de numai (2p) conditii.

Se presupune, pentru moment, ca se pot determina numai (p-1) armonici, deci 2(p-1) date, la care adaugand componenta continua, inseamna ca s-au valorificat doar (2p-1) conditii, una ramanand disponibila. Se admite ca aceasta conditie poate oferi un indiciu despre armonica de rang p, dar nu va permite o identificare completa a acesteia.

Pentru studiul analitic al identificarii particulare a armonicii de frecventa Nyquist, se recurge la calculul coeficientilor Fourier pentru cazul N=p. Se considera seria de esantioane

(2.82)

pentru care coeficientii Fourier (rel. 2.57) rezulta dupa cum urmeaza:

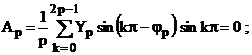(2.83)

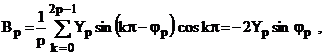(2.84)

care arata ca numai B_p 0 (A_p=0), pentru cazul , dar nici amplitudinea si nici faza nu pot fi calculate corect. Comparand cu relatia (2.74), se observa ca B_p rezulta de o valoare dubla fata de cea care ar fi normala (a se vedea si exemplul din tab. 2.3).

In concluzie, armonica de frecventa Nyquist nu este determinabila, putandu-se evidentia cel mult ca aceasta exista, daca intamplator faza acesteia este diferita de zero sau p. S-a argumentat astfel suficient ca rangul maxim al armonicii determinabile, in cazul undelor esantionate este

(2.85)

fapt de care s-a tinut seama in scrierea relatiilor (2.57).

Faza aparenta j_p a armonicii cu frecventa Nyquist rezulta, conform relatiilor (2.83) si (2.84):

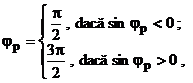(2.86)

daca analiza armonica s-ar face totusi pana la N=p.

4. Translatarea armonicilor nedetectabile

Un aspect deosebit de interesant, detectat cu ajutorul programului pe calculator (REGIDE - original, in LabVIEW), il reprezinta identificarea ca armonica de ordin inferior, K< p, a unei armonici care are in realitate un ordin M, mai mare decat limita detectabila, M>p. Acest fenomen, cunoscut in literatura de specialitate ca efect alias sau efect de repliere sau chiar redefinire 10,52 , distorsioneaza sau 'falsifica' identificarea.

Pentru evidentierea fenomenului, se considera o armonica de un rang N suficient de mare (ex. N=17), cu amplitudine si faza cunoscute (rel. 2.15), care este mai intai esantionata, cu numere de diviziuni (2p) diferite, astfel incat sa fie intalnite toate situatiile posibile p<N, p=N si p>N. S-au ales pentru N si p numere nu prea mari, din motive de simplitate. Trebuie remarcat faptul ca, in programul de analiza armonica, se introduce tot seria de esantioane a functiei de analizat, ca in cazurile practice, si nu expresia analitica y_A a acesteia.

In tabelul 2.3 se prezinta rezultatele rularii succesive a programului de identificare a undei

y_A=5sin(17x+p/3), (2.87)

cu un numar variabil de esantioane pe semiperioada (NP). Se observa ca, desi unda analizata reprezinta o armonica de rang N=17, aceasta este identificata ca fiind de ranguri inferioare, KI, atunci cand numarul de esantioane pe o semiperioada ia respectiv valorile pI, deci cand p<N. Amplitudinea insa este corect identificata (C =Y₁₇ =5,00).

In al doilea rand, se remarca identificarea incorecta a amplitudinii pentru cazul cand rangul armonicii este egal cu numarul de esantioane/semiperioada (N=p, armonica de frecventa Nyquist), ceea ce confirma una din observatiile anterioare (par. 3), referitoare la rangul maxim identificabil si constituie o verificare numerica pentru relatia (2.84). In fine, pentru p 18>N=17, identificarea se face corect.

Identificarea unei armonici de un rang dat (N=17), in functie de

numarul de esantioane pe perioada

Tabelul 2.3

Fenomenul identificarii unei armonici superioare, nedetectabile ('invizibile') ca o armonica de ordin inferior a fost pus in evidenta si in cazul unei unde cu o compozitie armonica mai complexa, cand s-a observat faptul ca fenomenul translatarii unei armonici nedetectabile este insotit de compunerea armonicii alias (translatate) cu armonica de rang inferior (K<p), existenta realmente in unda de analizat.

Justificarea analitica a posibilitatii de aparitie a efectului alias si a modalitatii de manifestare a acestuia se bazeaza pe considerarea sirului de esantioane ale unei armonici de rang M>p sub forma

(2.88)

pentru care se pune problema daca poate sa apara, in urma analizei Fourier discrete, ca o armonica de ordinul N. Se calculeaza asadar coeficientii Fourier A_N si B_N cu relatiile cunoscute (2.57), dar pentru sirul de esantioane dat de relatia (2.88). Desi se cunoaste faptul ca, pentru o armonica de rang M N si M<N, coeficientii A_N si B_N sunt nuli, se cauta acele cazuri particulare, cand coeficientii pot fi nenuli. Dupa transformari elementare, relatiile pentru coeficientii A_N si B_N se obtin, in acest caz, sub forma:

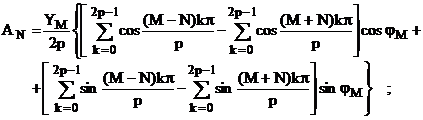(2.89)

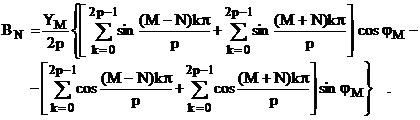(2.90)

Utilizand transformari conform relatiilor (2.71) si (2.72), se obtine ca, pentru numere J intregi, care nu sunt divizibile cu p, sumele de forma de mai jos sunt nule:

(2.91)

astfel ca ca A_N si B_N sunt nuli, inclusiv pentru cazul M< N.

Daca insa M> N si (2p) (M N), coeficientii Fourier, calculati cu relatiile (2.89) si (2.90), pot avea una dintre urmatoarele forme:

- daca (2p) (M-N),

(2.92)

- daca (2p) (M N

(2.93)

confirmandu-se analitic posibilitatea de aparitie a efectului alias [52].

Asadar, conditia ca o armonica de ordinul M>p sa apara ca o armonica de ordinul N<p, atunci cand pe o perioada a undei analizate se folosesc (2p) esantioane, se exprima analitic prin relatia

(2p) | (M N), (2.94)

adica, astfel ca numarul intreg (M N) sa se divida prin (2p).

In 54 , s-a propus ca relatie de determinare a frecventei aparente (alias) f_NA valoarea absoluta a diferentei dintre cel mai mic multiplu al frecventei de esantionare si frecventa reala a armonicii respective:

(2.95)

in care f_e este frecventa de esantionare, f_M - frecventa reala a armonicii de rang M, iar K_min - cel mai mic (apropiat) numar intreg, care duce la satisfacerea egalitatii. Se poate constata ca relatiile (2.94) si (2.95) sunt echivalente.

Datorita fenomenului de translatare a armonicilor nedetectabile, corectitudinea analizei Fourier, discrete, a unui sir de esantioane poate fi pusa la indoiala. Garantarea corectitudinii analizei poate fi facuta in urmatoarele doua feluri, urmand variantele de algoritmi propuse in continuare:

- realizarea esantionarii la o frecventa ridicata, pentru a se putea alege din sirul complet de valori subsiruri de esantioane cu numere de valori diferite. Diferentele dintre analizele armonice ale doua subsiruri diferite ar putea pune in evidenta existenta unor armonici nedetectabile in compunerea undei studiate, iar identitatea rezultatelor ar confirma justetea determinarii. In cazurile in care exista diferente la amplitudinile unor armonici, inseamna ca exista armonici superioare, repliate (translatate), al caror ordin poate fi determinat cu relatii de forma (2.94) sau (2.95);

- generarea, pe baza sirului de esantioane achizitionat si a unei metode de interpolare, a unor siruri de valori cu numere diferite de elemente (esantioane) si aplicarea analizei armonice pentru fiecare din aceste siruri, cu compararea rezultatelor si cu consecinte ca mai sus.

Din punct de vedere practic, este insa mai eficient si comod, daca ininte de a accesa la placa de achizitie, semnalele ar fi trecute print-un filtru trece jos, care sa limiteze frecventa maxima a semnalelor care urmeaza sa fie achizitionate si deci analizate.

5. Cerinte pentru programele de analiza asistata

Importanta analizei armonice si frecventa utilizarii acesteia rezida in problemele de calitate a energiei electrice, in aparitia tot mai extinsa a regimurilor deformante si din necesitatea limitarii acestora. O analiza armonica veridica si cat mai exacta este absolut necesara pentru cunoasterea situatiei reale, aprecierea cauzelor perturbatiilor si pentru evidentierea corecta a masurilor de limitare si diminuare a regimului deformant [5,10].

Principalele cerinte pentru o analiza armonica utila pot fi formulate astfel [44]:

identificarea corecta a amplitudinilor si fazelor tuturor armonicilor prezente in unda de analizat;

neglijarea armonicilor cu amplitudini nesemnificative, situate in domeniul de eroare a metodei de determinare;

reconstituirea undei din armonicile identificate si compararea cu unda de analizat, cu determinarea abaterii medii patratice dintre acestea, dupa fiecare pas de identificare a unei noi armonici si oprirea calculului atunci cand abaterea medie patratica este zero sau minima;

posibilitatea etalonarii aparatului sau echipamentului;

evidentierea situatiilor in care armonici superioare sau interarmonici, prezente in unda de analizat, nu sunt determinate si identificarea acestora;

realizarea calculelor intr-un timp cat mai redus posibil, pentru ca rezultatele sa poata fi utilizate in timp cvasireal (dupa cel mult o perioada din momentul terminarii achizitiei).

Dupa cum s-a aratat (par. 1), utilitatea analizei armonice in tehnica este pentru functii esantionate, fie ca acestea sunt introduse in calculator printr-un sistem de achizitie DAQ sau din memoria unor aparate de masura perfectionate (ex. osciloscop digital, calimetru - powermeter, osciloperturbograf), fie ca se introduc de la tastatura, in urma prelucrarii unor inregistrari grafice. In plus, un program pe calculator pentru analiza armonica ar trebui sa indeplineasca cel putin primele patru dintre cele sase cerinte expuse anterior.

Daca prima cerinta, aceea a identificarii corecte a amplitudinilor si fazelor tuturor armonicilor pana la ordinul maxim (p-1) a fost solutionata (scap. 1), iar cerinta a doua, referitoare la neglijarea armonicilor cu amplitudini nesemnificative, este extrem de usor de implementat, cea de a treia cerinta, avand ca idee centrala reconstituirea undei, prezinta o serie de implicatii care se impun a fi detailate.

S-a subliniat deja necesitatea unui criteriu tehnic fundamentat pentru oprirea analizei armonice, nefiind rationala continuarea analizei din momentul in care unda reconstituita este identica cu cea analizata. Astfel, dupa fiecare pas de determinare a marimilor caracteristice ale unei armonici de rang oarecare N, se pot calcula cele 2p ordonate ale undei reconstituite din armonicile identificate pana in acel moment. In continuare, se poate calcula abaterea medie patratica dintre valorile YA_k ale undei analizate (ordonatele initiale) si cele ale undei reconstituite Y_k:

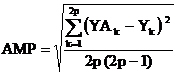. (2.96)

Valoarea minima a abaterii medii patratice este relevanta pentru calitatea analizei armonice, astfel:

-daca valoarea finala, minima, a abaterii medii patratice este zero, inseamna ca s-au gasit toate armonicile existente in unda de analizat si ca analiza armonica este veridica si completa;

-daca valoarea minima a abaterii medii patratice este diferita (mai mare) de zero, inseamna ca mai sunt armonici neidentificate si deci numarul de puncte (2p) trebuie marit corespunzator, pana la identificarea tuturor armonicilor; se subliniaza, inca o data, ca analiza Fourier discreta poate determina maximum (p-1) armonici. Daca insa unda analizata contine interarmonici, atunci este necesara reanalizarea marimii perioadei, care se considera pentru fundamentala.

Reconstituirea undei dupa fiecare iteratie de identificare a unei armonici permite folosirea criteriului abaterii medii patratice minime pentru oprirea calculelor, chiar daca nu s-a ajuns la rangul maxim, determinabil al armonicilor. Daca in plus, determinarea parametrilor (Y_N, j_N) ai armonicilor s-a facut corect pentru toate componentele undei reale, valoarea minima a abaterii medii patratice, pentru care analiza are sens sa fie oprita, este egala cu zero; in acest caz, s-au identificat corect toate armonicile din compunerea undei analizate.

Validarea corectitudinii analizei armonice si prin aceasta etalonarea aparatului (conditia a patra) se poate face numai pentru unde cu compozitii armonice cunoscute, cu conditia ca algoritmul de prelucrare sa contina urmatoarele etape principale:

scrierea formei analitice a marimii pulsatorii cu compozitia armonica dorita;

esantionarea marimii pulsatorii cu numarul de diviziuni (2p) stabilit dupa caz sau dorinta;

analiza armonica a marimii esantionate;

reconstituirea undei si compararea cu unda analizata.

Initial, programul original (REGIDE) a fost implementat in limbajul C, dar ulterior, data fiind utilitatea instrumentatiei virtuale pentru aspectele de calitate a energiei electrice si disponibilitatea la reprezentari grafice, s-a trecut in mediul de dezvoltare LabVIEW.

Exista echipamente care pot genera unde cu compozitii armonice alese dupa dorinta, care pot fi conectate direct la montajul cu traductoare si placa de achizitii, rezultatele analizei armonice putand fi comparate cu datele caracteristice ale undei generate.

6. Caracteristici ale analizei asistate

Observarea unor serii de esantioane poate fi interesanta pentru orice specialist si chiar relevanta, in anumite etape ale analizei armonice. Pentru aceasta, se considera o unda cu o compozitie armonica determinata (cunoscuta), pentru care se reprezinta seriile de esantioane specifice pasilor caracteristici, ai unei analize armonice. S-a apreciat ca, prin paralela metodologica dintre analitic si grafic, se asigura o mai buna percepere a particularitatilor analizei armonice.

a) Date initiale

Fie o unda alternativa, cu compozitie armonica cunoscuta, data de expresia

, (2.97)

care contine, pe langa fundamentala, armonicile de ordinele 2, 3 si 7. Seria de esantioane aferente acestei functii, reprezentand datele initiale ale analizei armonice, este redata in figura 2.19 pentru numarul de diviziuni 2p=20, suficient de mare pentru a identifica toate armonicile (N_Max=7 < 10) prezente.

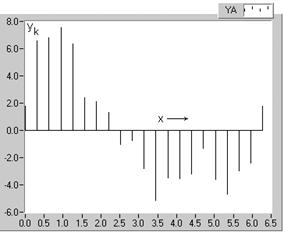
Fig. 2.19. Seria de esantioane corespunzatoare undei analizate, pentru cazul p=10.

Pentru a aprecia contributia fiecarei armonici la stabilirea valorilor esantioanelor corespunzatoare functiei de analizat, in figura 2.20 sunt reprezentate seriile de esantioane ale fundamentalei (fig. 2.20,a), precum si cele ale armonicilor componente.

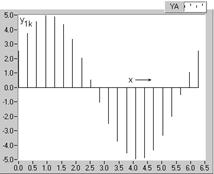
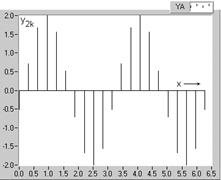
a 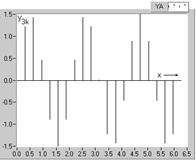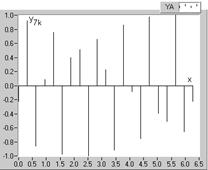b

c d

Fig. 2.20. Seriile de esantioane corespunzatoare componentelor undei analizate:

a-pentru fundamentala; b-armonica a doua; c-armonica a treia; d-armonica a saptea.

De remarcat faptul ca periodicitatea este observabila pentru fundamentala (fig. 2.20, a) si pentru armonicile de ordinul doi (fig. 2.20, b) si trei (fig. 2.20, c), in timp ce pentru armonica de ordinul N=7, datorita numarului relativ redus de diviziuni (2p=20), periodicitatea este mai putin evidenta. Esantioanele functiei de analizat (fig. 2.19) sunt respectiv suma algebrica a esantioanelor corespunzatoare componentelor (fig. 2.20), conform relatiei (2.97).

b) Rezultate intermediare

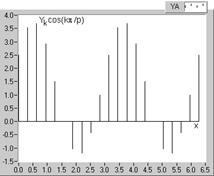
Pentru a patrunde in mecanismul analizei armonice, s-a considerat utila reprezentarea termenilor sumelor din relatiile (2.57), deci a esantioanelor functiei de analizat (fig.2.19), multiplicate cu valorile functiilor de modulatie sin(Nx), respectiv cos(Nx). In figura 2.21 sunt redate cele doua serii de esantioane, determinate pentru cazul functiilor de modulatie, corespunzatoare extragerii fundamentalei (N=1), care sunt sinx (fig. 2.21,a), respectiv cosx (fig. 2.21,b). Sumele valorilor acestor esantioane stau la baza determinarii coeficientilor Fourier A₁ si B₁, respectiv; se poate aprecia de pe grafice faptul ca ambii coeficienti, A₁ si B₁, sunt pozitivi.

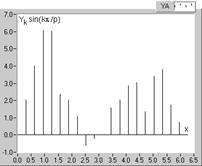
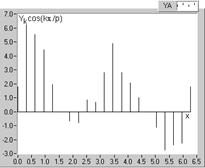
a b

Fig. 2.21. Seriile de esantioane ale undei analizate, modulate cu functiile armonice pentru

extragerea fundamentalei: a-modulatia cu functia sinx; b-idem, cosx.

Esantioanele Y_k ale functiei de analizat (fig. 2.19) sunt sume algebrice ale esantioanelor corespunzatoare componentelor (Y_1k, Y_2k, Y_3k, si Y_7k, fig. 2.20), iar functiile de modulatie conduc la sume de forma (2.57), nule, atunci cand moduleaza armonici de ordin diferit de al lor; prin urmare, seriile de esantioane ale fundamentalei (fig. 2.20, a), modulate tot cu functiile de modulatie, corespunzatoare extragerii fundamentalei, sinx, respectiv cosx (x=kπ/p, k=0, 1, , 2p-1), ca mai sus, conduc tot la obtinerea coeficientilor Fourier A₁ si B₁. De observat insa ca seriile de esantioane corespunzatoare, din figurile 2.21 si 2.22, desi conduc la rezultate identice si au aspect relativ asemanator, reprezinta de fapt serii distincte de valori.

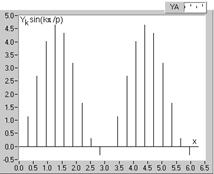
a b

Fig. 2.22. Seriile de esantioane ale fundamentalei (fig.2.20, a), modulate cu functiile

armonice corespunzatoare: a - sinx; b - cosx.

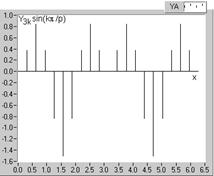
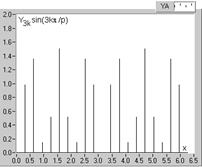
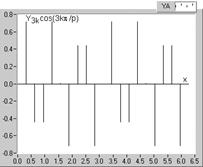
Un alt aspect, considerat interesant, se refera la seriile de esantioane corespunzatoare unei armonici; s-a luat spre exemplificare armonica de ordinul trei, pentru care s-au reprezentat in figura 2.23 trei serii de esantioane, astfel:

seria de esantioane ale armonicii de ordinul trei, modulata cu functia sinx, corespunzatoare fundamentalei (fig. 2.23, a). Analitic, se poate verifica faptul ca suma acestei serii de esantioane este nula; examinand numerele de esantioane pozitive si negative, precum si marimile acestora, se poate admite, chiar numai prin examinarea graficului, ca aceasta conditie este indeplinita;

aceeasi serie de esantioane, modulata cu functia sin(3x) (fig. 2.23, b). Suma acestei serii este evident strict pozitiva;

aceeasi serie de esantioane, modulata cu functia cos(3x) (fig. 2.23, c). Suma acestei serii este destul de evident nula, avand in vedere faptul ca numerele de esantioane pozitive, respectiv negative, de valori identice, sunt egale. In consecinta, coeficientul Fourier B₃ rezulta nul, ceea ce corespunde, impreuna cu remarca anterioara, cazului de faza nula a armonicii de ordinul trei, asa cum apare si in expresia (2.97).

a

b c

Fig. 2.23. Seriile de esantioane ale armonicii de ordinul trei (fig.2.20, c), din unda analizata, modulate cu functii armonice: a-functia de modulatie sinx, corespunzatoare fundamentalei; b-functia de modulatie sin(3x); c-modulatie prin cos(3x).

c) Rezultate finale

Marimea caracteristica pentru o unda pulsatorie sau alternativa, care se poate calcula din seria de valori ale esantioanelor undei de analizat, este reprezentata de valoarea efectiva Y_ea a undei analizate, data de relatia

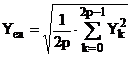; (2.98)

aceasta valoare, determinabila chiar inainte de inceperea analizei armonice, poate fi folosita ca referinta si in programele de analiza armonica, pentru evaluarea stadiului de reconstituire a undei.

Astfel, considerand determinate componenta continua Y₀ si amplitudinile Y_N, si calculand valorile efective Y_eN ale armonicilor cu relatia

, (2.99)

valoarea efectiva a undei reconstituite se determina cu expresia

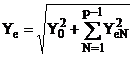, (2.100)

marime care tinde spre Y_ea cu fiecare iteratie de determinare a unei noi armonici si este egala cu Y_ea in cazul identificarii complete.

In tabelul 2.4 se prezinta protocolul de analiza armonica a unei unde cu compozitie armonica cunoscuta (rel. 2.97), varianta utilizata pentru validarea metodei si evidentierea unor aspecte mai putin cunoscute. Se reaminteste faptul ca programul utilizat are intercalata etapa de esantionare intre etapele de definire analitica a functiei si de analiza armonica (asa cum s-a precizat la par. 5).

Protocolul de analiza armonica pentru o marime alternativa

cu compozitie armonica cunoscuta.

Tabelul 2.4

Eroarea relativa de redare a functiei ERR se adopta de catre utilizator (in cazul considerat ERR=0.005, adica 0.5%), iar in functie de aceasta se calculeaza eroarea absoluta ERA, definita prin relatia

ERA = YEF * ERR (2.101)

in care YEF reprezinta valoarea efectiva Y_ea a undei analizate (rel. 2.98). Toate armonicile cu amplitudini mai mici decat ERA urmeaza a fi ignorate, nefiind luate in calcule si nici trecute pe protocolul cu rezultate (listing). In acest fel, rezultatul analizei armonice se dezvaluie in aspectele sale esentiale, nediluate intr-un volum de date nesemnificative.

Numarul de diviziuni pe o semiperioada, utilizat pentru esantionarea marimii analitice, este precizat prin NP=p.

In continuare, in tabel, se prezinta rezultatele analizei armonice, cuprinzand:

-ordinele K ale armonicilor identificate;

-amplitudinile C si fazele FI ale armonicilor;

-valoarea efectiva YAE a undei reconstituite si abaterea medie patratica AMP dintre valorile esantioanelor si valorile undei reconstituite, dupa fiecare pas de identificare a unei noi armonici;

-in final, se prezinta valorile rezidului deformant Y_def, a factorului de distorsiune THD si durata analizei armonice TAnaliza [42].

7. Indicatori ai regimului deformant

Stabilirea indicatorilor caracteristici pentru abaterile undelor de la forma ideala, sinusoidala se bazeaza fie pe valorile admisibile ale armonicilor de curent sau tensiune, fie pe parametrii sintetici ai distorsiunii. Daca unii indicatori pot fi determinati atat pentru tensiuni cat si pentru curenti, exista indicatori care au sens numai pentru unda de tensiune.

a) Nivelul γ_N al armonicii de ordinul N, se defineste ca raportul, exprimat in procente, dintre valoarea efectiva Y_eN a armonicii si valoarea efectiva Y_e a undei

(2.102)

in care Y_eN se obtine impartind cu amplitudinea Y_N, calculata cu relatia (2.61), iar valoarea efectiva Y_e a undei analizate se poate calcula din sirul de 2p valori cu relatia (2.98), deci se poate lua Y_e= Y_ea sau folosind rezultatul unei analize Fourier complete (componenta continua plus (p-1) armonici), conform relatiei:

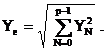(2.103)

Uneori, in relatia (2.102), in locul valorii efective Y_e a undei se foloseste valoarea efectiva a fundamentalei Y_e1. De remarcat ca determinarea valorii efective a undei cu relatia (2.98) poate fi facuta inca inainte de inceperea analizei armonice, iar valoarea aceleiasi marimi, calculata cu relatia (2.103), constituie o masura a incheierii corecte a analizei, daca rezulta egala sau aproximativ egala cu valoarea efectiva, data de relatia (2.98).

a) Reziduul deformant se defineste prin expresia

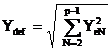(2.104)

putand fi calculat, de asemenea, imediat dupa identificarea componentelor continua Y₀ si a valorii efective a fundamentalei Y_e1, cu relatia

(2.105)

avand in vedere ca si Y_ea este deja determinata cu relatia (2.98).

c) Factorul de distorsiune (in engleza, the Total Harmonic Distortion - THD) al unei unde nesinusoidale este definit prin raportul, exprimat in procente, dintre reziduul deformant si valoarea efectiva a fundamentalei

(2.106)

in literatura de specialitate, in locul valorii efective a fundamentalei se foloseste, uneori, valoarea nominala, mai ales daca marimea Y desemneaza o tensiune.

In privinta curentilor, s-a constatat ca la valori mici ale acestora, factorul de distorsiune (THD) poate fi mare, desi situatia nu reprezinta o solicitare semnificativa a instalatiei sau a echipamentului. Pentru ca distorsiunea sa fie interpretabila, s-a considerat oportuna raportarea reziduului deformant al curentului la curentul cerut I_c, corespunzator duratei conventionale de 15 sau 30 min, obtinandu-se factorul notat cu TDD_I (in engleza, the Total Demand Distorsion):

(2.107)

d) Factorul de varf se defineste ca raportul dintre valoarea maxima Y_max si valoarea efectiva Y_e, ale undei analizate:

, (2.108)

valoarea maxima Y_max fiind determinata din sirul de esantioane Y_k ale undei de analizat

_{8. Valori limita ale indicatorilor de regim deformant}

Regimul deformant reprezinta actualmente aspectul de CEE, pentru care se face cea mai larga detaliere a valorilor limita ale indicatorilor in reglementari si standarde. Sunt precizate limite pentru factorii de distorsiune si pentru nivelul armonicilor, atat pentru tensiuni cat si pentru curenti [10,12]. Fara a se urmari o prezentare exhaustiva a normarii indicatorilor de regim deformant pe plan international, se retin in continuare cateva din modalitatile de limitare a emisiei si circulatiei de armonici de curent sau tensiune.

Astfel, in tabelul 2.5 sunt indicate valorile limita ale factorului de distorsiune pentru armonicile de tensiune [12], iar in tabelul 2.6 - pentru armonicile de curent, conform [22].

Normele interne limiteaza factorul de distorsiune al curbelor de tensiune astfel:

, pentru retele de joasa si medie tensiune;

, pentru retele de inalta tensiune.

Se preconizeaza deja ca limitele perturbatiilor sa fie diferentiate pentru receptoare individuale si consumatori in ansamblu, precum si in raport cu modul de masurare [10].

Factorii de distorsiune limita pentru unde de tensiune

Tabelul 2.5

Nivelurile limita pentru armonicile de curent si factorii de distorsiune limita pentru curenti (raportare la valoarea efectiva a fundamentalei)

Tabelul 2.6

¹⁾-curentul de scurtcircuit maxim in punctul de racord; -curentul cerut de sarcina perturbatoare in punctul comun de racord;

²⁾Armonicile pare sunt limitate la 0,25 din nivelurile limita admise pentru armonicile impare.