
|
|
|
DECODIFICATOARE
l. INTRODUCERE
Aplicatia isi propune sa puna in practica notiunile teoretice referitoare la functii logice, notiuni legate de:
reprezentarea functiilor logice;
minimizarea functiilor logice prin diagrame Karnaugh;
implementarea functiilor logice.
Decodificatoare
2. CONSIDERATII TEORETICE
Tabelul de adevar este un tablou avand, pentru o functie de n variabile, 2n linii corespunzand tuturor combinatiilor posibile ale valorilor argumentelor - si n+1 coloane, primele n pentru variabile si ultima pentru valorile functiei (fig. 1).

Fig. 1- Tabel de adevar
Daca functia este complet definita, atunci toate valorile ei sunt cunoscute. Exista functii logice incomplet definite, la care, pentru anumite combinatii ale valorilor argumentelor nu se cunoaste cu exactitate valoarea functiei, Aceste situatii de nedefinire se evidentiaza prin plasarea unui asterisc (*) in dreptul combinatiei respective, in coloana valorilor functiei.
Diagrama Kamaugh este o reprezentare tabelara mai compacta, pe doua dimensiuni. Combinatiile valorilor argumentelor sunt in codul Gray. Pentru o functie de n variabile diagrama are 2n campuri (fig. 2). Completarea diagramei se poate face cu usurinta pornind de la tabelul de adevar.
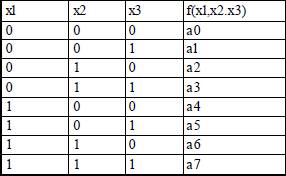
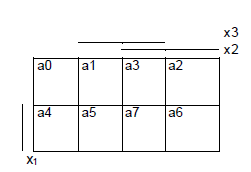
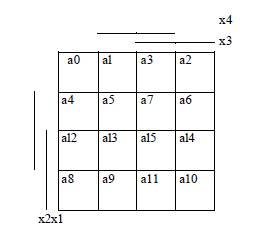
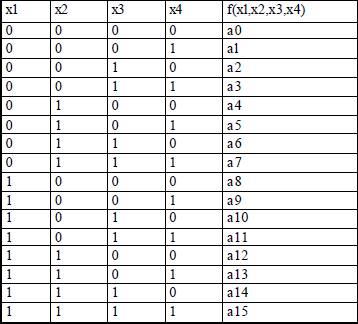
Fig 2.- Diagrama Kamaugh
In exteriorul unei diagrame Karnaugh, un segment inseamna '1' logic iar un spatiu '0' logic pentru variabila respectiva. Completarea diagramei depinde de amplasarea variabilelor in exterior. Daca functia este incomplet definita,
unele campuri vor contine asteriscuri(*).
Formele canonice (forma canonica disjunctiva - FCD si forma canonica conjunctiva -FCC) sunt reprezentari care constau in sume logice (FCD) sau produse logice (FCC) de termeni canonici. Acestia contin toate variabilele functiei, ca atare sau negate, fiind la randul lor de doua tipuri:
termeni canonici disjunctivi (TCD), reprezentand sume logice ale tuturor variabilelor avand notatia prescurtata Sk;
termeni canonici conjunctivi (TCC), reprezentand produse logice ale tutun variabilelor, avand notatia prescurtata Pk.
Astfel, se poate scrie pe scurt: FCD = SSk; FCC = PPk.
Formele canonice se determina astfel:
Forma canonica disjunctiva (FCD):
1. se cauta in tabelul de adevar valorile de '1' logic ale functiei;
2. pentru fiecare dintre aceste valori se scrie combinatia binara corespunzatoare valorilor variabilelor functiei;
3. fiecarei combinatii binare de mai sus ii corespunde un TCC, care se scrie astfel:
4. daca unei variabile ii corespunde in combinatia respectiva o valoare de '1' logic atunci aceasta variabila se scrie ca atare;
5. daca unei variabile ii corespunde in combinatia respectiva o valoare de '0' logic atunci aceasta variabila se scrie complementata.
6. se scrie reuniunea tuturor TCC astfel determinati.
Forma canonica conjunctiva (FCC):
1. se cauta in tabelul de adevar valorile de '0' logic ale functiei;
2. pentru fiecare dintre aceste valori se scrie combinatia binara corespunzatoare valorilor variabilelor functiei;
3. fiecarei combinatii binare de mai sus ii corespunde im TCD, care se scrie astfel:
4. daca unei variabile ii corespunde in combinatia respectiva o valoare de '1' logic atunci aceasta variabila se scrie ca atare;
5. daca unei variabile ii corespunde in combinatia respectiva o valoare de '0' logic atunci aceasta variabila se scrie complementata.
6. se scrie intersectia tuturor TCD astfel determinati.
Indicele k din notatiile Pk si Sk reprezinta echivalentul zecimal al combinatiei binare corespunzatoare termenului canonic respectiv.
Daca se are in vedere criteriul economic, reprezentarea prin FCD se prefera atunci cand functia are putine valori de '1' logic, iar reprezentarea prin FCC atunci cand functia are putine valori de '0' logic.
2.2 Minimizarea functiilor logic
Minimizarea urmareste materializarea economica a functiilor logice, prin reducerea numarului de termeni si a
numarului de variabile ale termenilor.
2.2.1 Minimizarea folosind diagrama Karnaugh
Oricare doua campuri alaturate sau situate la capetele aceleasi linii sau aceleasi coloane sunt numite campuri vecine. Aceste campuri au proprietatea de adiacenta, adica la trecerea dintr-un camp in unul vecin doar o singura variabila isi modifica valoarea logica. Minimizarea foloseste gruparea campurilor vecine care contin valori identice ale functiei. Campurile vecine se pot grupa doar intr-un numar egal cu o putere a lui 2 (1,2, 4, 8,..), rezultatul gruparii fiind eliminarea acelei sau acelor variabile care isi modifica valoarea logica la trecerea dintr-un camp in altul al respectivei grupari. Forma minima rezulta prin asocierea termenilor corespunzatori gruparilor.
Minimizarea dupa '1' logic:
se grupeaza campurile cu valori de '1' logic, intr-un numar egal cu o putere a lui 2;
se pastreaza doar variabilele care nu-si schimba valoarea logica in campurile gruparii respective, scriindu-le sub forma unui produs logic in care:
variabila careia ii corespunde un segment se scrie ca atare;
variabila careia ii corespunde un spatiu se scrie complementata;
se scrie suma logica a termenilor obtinuti rezultand expresia minimala disjunctiva.
Minimizarea dupa '0' logic:
se grupeaza campurile cu valori de '0' logic, intr-un numar egal cu o putere a lui 2;
se pastreaza doar variabilele care nu-si schimba valoarea logica in campurile gruparii respective, scriindu-le sub forma unei sume logice in care:
variabila careia ii corespunde un spatiu se scrie ca atare;
variabila careia ii corespunde un segment se scrie complementata;
se scrie produsul logic al termenilor obtinuti rezultand expresia minimala conjunctiva.
Observatie. Mai multe grupari pot avea campuri comune, cu conditia ca fiecare grupare sa posede si macar un camp propriu (care sa nu mai apartina altei grupari).
3. Generalitati
Codarea este aplicatia ce stabileste o corespondenta intre elementele unei multimi-sursa (care este in general o submultime a multimii numerelor rationale) si elementele unei multimi-destinatie (care cuprinde combinatii ordonate de valori 0 si 1, numite cuvinte-cod). Codorul este dispozitivul ce traduce valorile unei intrari intr-un cod ales.
Decodarea este aplicatia inversa codarii, decodorul (decodificatorul) fiind circuitul ce furnizeaza o informatie atunci cand combinatia variabilelor binare ce i se aplica pe intrari reprezinta un cuvant-cod (adresa).
Cele doua aplicatii sunt prezentate in Fig. 3.
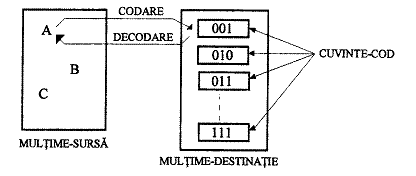
Fig. 3 Codare si Decodarea
In practica se intalnesc doua tipuri de decodari:
1. decodarea unei combinatii binare determinate (decodare elementara). Decodarea se obtine cu ajutorul unei simple porti SI care verifica simultaneitatea valorilor variabilelor binare pentru configuratia ce trebuie decodata.
2. decodarea tuturor combinatiilor unui cod (decodare completa). In acest caz, sistemul contine, pentru m adrese, m decodificatoare elementare, deci exista m iesiri.
Cum combinatia variabilelor binare de intrare este stabila si unica la un moment dat, doar o singura iesire va fi in stare activa, toate celelalte iesiri fiind inactive (fig.4).Se pot realiza atat decodificatoare cu iesirile active in '1' logic cat si decodificatoare cu iesirile active in '0' logic (care in acest caz se marcheaza cu un cerculet).
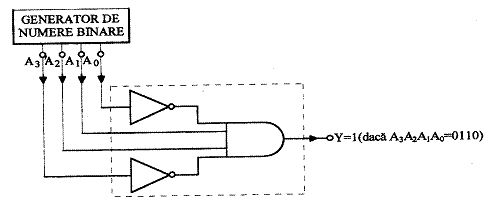
Fig. 4 Decodificator cu iesire activa
3.1 Decodificatorul binar complet (de adresa) de 2 biti
In acest caz pot fi decodificate 22=4 adrese. Schema bloc si tabelul de adevar ale circuitului sunt prezentate in Fig. 5 (s-au considerat iesirile active in '1' logic tabelul de adevar se deduc urmatoarele expresii logice pentru iesiri:
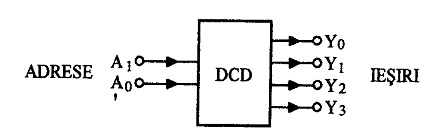
TABELUL DE ADEVAR
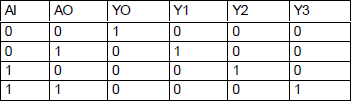
Fig. 5 Schema bloc si tabelul de adevar
Se observa ca un decodificator materializeaza termeni canonici de tip produs (PK). Fig. 6 prezinta schema logica a circuitului.
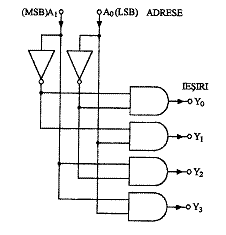
Fig. 6 Shema logica a circuitului
3.2 Decodificatorul BCD-zecimal (CDB 442E)
Acest circuit are 4 intrari (D=MSB, C, B, A=LSB), pe care se aplica la un moment dat o combinatie din codul BCD (0000, 0001,., 1001). Cele 10 iesiri sunt active in '0' logic (Fig. 7). Pentru combinatiile 1010,., 1111, care nu fac parte din codul BCD ('stari false'), toate iesirile raman in stare inactiva ('l' logic); se spune ca se face rejectia datelor false. Ca urmare, tabelul de adevar al decodificatorului va fi prezentat in tabelul 2.
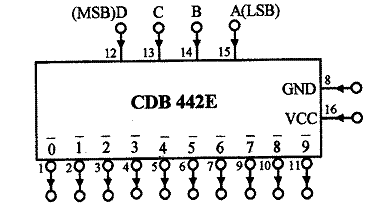
Fig. 7 Decodificatorul CDB 442E
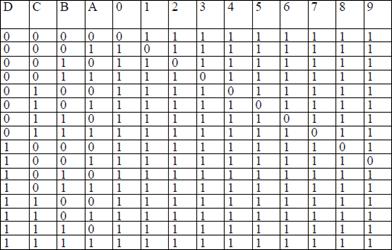
Tabel 2- Tabelul de adevar al decodificatorului
Expresiile booleene ale iesirilor decodificatorului sunt:

Structura se poate realiza deci cu inversoare si cu NAND-uri cu 4 intrari. Patru dintre inversoarele conectate pe intrari complementeaza variabilele de intrare, iar celelalte patru asigura incarcarea liniilor D, C, B, A cu o singura unitate de sarcina TTL.
Observatie. S-a putut remarca in cazul decodificatoarelor faptul ca, daca N este echivalentul zecimal al adresei, N10 = (An-1.A1A0)2 atunci iesirea activa va fi YN.
4. DESFASURAREA APLICATIEI
4.1 Studiul unei functii logice de 4 variabile
Realizarea legaturilor sunt prezentate in Fig. 8, acestea sunt realizate dupa parcurgerea urmatoarelor etape:
se procedeaza la identificarea functiei, construind tabelul de adevar se stabilesc cele 16 combinatii posibile ale variabilelor de intrare prin intermediul celor 4 minicomutatoare si se noteaza de fiecare data valoarea functiei;
pe baza tabelului de adevar se determina:
1. diagrama Karnaugh;
2. formele canonice;
se minimizeaza functia dupa '1' logic si dupa '0' logic, folosind diagrama Karnaugh;
se determina schema logica in functie de legaturile realizate
se scriu expresiile booleene corespunzatoare schemei logice
folosind proprietatile algebrei booleene se determina expresia functiei logice sub forma normala disjunctiva.
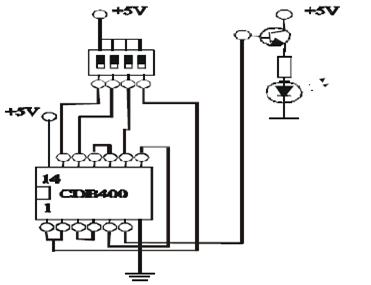
Fig. 8-Realizarea Legaturilor
4.2 Studiul decodificatorului BCD-zecimal (CDB 442)
Studiul decodificatorului BCD-zecimal (CDB 442) se face prin parcurgerea urmatoarelor etape:
se studiaza din catalog schema interna a circuitului.
se realizeaza legatura intrarilor cu cele patru comutatoare pentru adresare;
se alimenteaza montajul;
se parcurge intreaga gama a adreselor, urmarind starea celor zece iesiri;
se construieste tabelul de adevar al circuitului.
se studiaza posibilitatea de implementare cu decodificatoare a functiilor booleene
4.3 Realizarea unei functii logice folosind decodificatorul BCD-zecimal
Se realizeaza legaturile din Fig. 9.
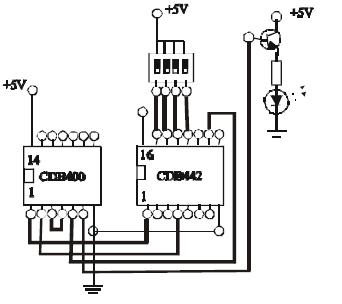
Fig. 9 Realizarea Legaturilor
Etapele realizarii unei functii logice:
1. se procedeaza la identificarea functiei, construind tabelul de adevar: se stabilesc cele 16 combinatii posibile ale variabilelor de intrare prin intermediul celor 4 minicomutatoare si se noteaza de fiecare data valoarea functiei;
2. pe baza tabelului de adevar se determina:
diagrama Karnaugh;
formele canonice;
3. se minimizeaza functia dupa '1' logic si dupa '0' logic, folosind diagrama Karnaugh;
4. se determina schema logica in functie de legaturile realizate
5. se scriu expresiile booleene corespunzatoare schemei logice
6. folosind proprietatile algebrei booleene se determina expresia functiei logice sub forma normala disjunctiva.