
|
|
|
Recapitulare componente pasive. Modelele simplificate
Rezistoare
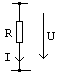
![]() ,
daca R este o constanta.
,
daca R este o constanta.
(In aceasta ecuatie au fost neglijate elementele reactive parazite si caracterul neliniar.)
In ecuatie timpul nu intervine in mod explicit; ea este valabila si sub forma:
![]()
Puterea instantanee disipata, in curent continuu: ![]() .
.
Energia disipata, in intervalul [0,t]: 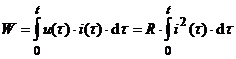
Puterea disipata, in
regim periodic: 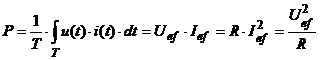 ,
unde valorile efective (sau eficace) sint definite prin:
,
unde valorile efective (sau eficace) sint definite prin: 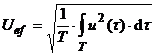 ,
, 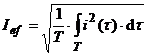
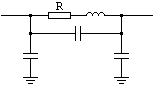
Elemente reactive parazite:
capacitate parazita intre terminale
capacitati parazite intre terminale si masa
inductanta parazita (mai insemnata la rezistoarele bobinate).
Limite de functionare:
temperatura interna la functionare (depinde de puterea disipata si de temperatura externa, deci limiteaza puterea maxima disipata)
temperatura de depozitare
puterea dispata (depinde de temperatura capsulei)
Caracteristica tipica a puterii disipate maxime, in functie de temperatura mediului:
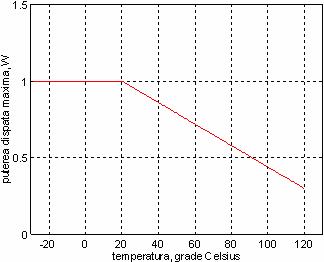
Caracterul neliniar:
dependenta rezistentei de temperatura influentata - la rindul ei - de puterea disipata)
dependenta rezistentei de tensiune (varistoare).
Exemplu: Dependenta de temperatura a rezistentei unui bec (baretor), 6V/50 mA
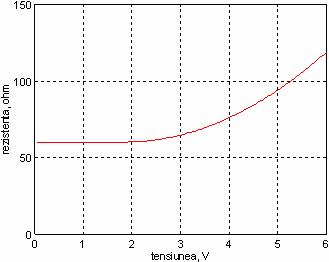
Condensatoare
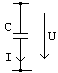
![]() sau
sau ![]() .
.
![]()
(In aceasta ecuatie au fost neglijate elementele reactive si disipative parazite si caracterul neliniar.)
Timpul intervine in mod explicit, ca expresie a fenomenului de acumulare de energie. Se zice ca aceasta componenta are caracter reactiv.
Ecuatia este o ecuatie diferentiala ordinara, liniara, de odinul I. Nu ne este suficienta solutia generala a ecuatiei (care este o familie de functii), ci dorim solutia problemei Cauchy.
Problema Cauchy:
![]()
![]() cunoscuta, unde
cunoscuta, unde ![]() este un moment arbitrar, in care
cunoastem valoarea tensiunii pe condensator.
este un moment arbitrar, in care
cunoastem valoarea tensiunii pe condensator.
Solutia: 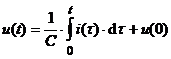 .
.
Daca u(t) este semnal sinusoidal, in regim permanent: ![]() ,
unde frecventa, perioada si pulsatia sint legate prin
relatiile:
,
unde frecventa, perioada si pulsatia sint legate prin
relatiile: ![]() si
si ![]() .
.
Atunci curentul este: ![]() .
.
Se observa ca cele doua marimi sint de aceeasi forma, dar defazate cu un sfert de perioada (curentul defazat inaintea tensiunii).
Defazajul se poate exprima
si in timp: ![]() .
.
In figura, semnal sinusoidal de perioada 1,25 ms (frecventa 800 Hz).
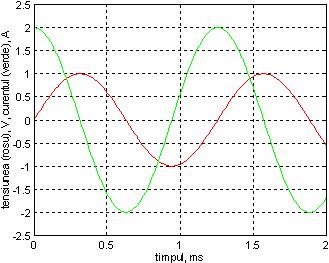
Raportul dintre amplitudinile tensiunii si curentului are dimensiunea unei impedante:
![]()
Pentru a exprima ambele proprietati (modul si defazaj), se foloseste reprezentarea in numere complexe:
![]() , unde j este
unitatea imaginara.
, unde j este
unitatea imaginara.
Condensatorul inmagazineaza energie:
![]()
(Pentru demonstratie, se poate presupune ca
tensiunea initiala pe condensator este nula, dupa care el
este incarcat la curent constant, pina la tensiunea U. Tensiunea variaza liniar, iar
incarcarea dureaza timpul ![]() .
Atunci, energia inmagazinata este:
.
Atunci, energia inmagazinata este: 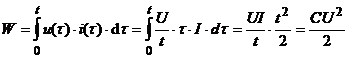 )
)
Condensatorul ideal nu disipa energie. Condensatorul real presupune si efect disipativ, datorita pierderilor in dielectric, prin conductie si prin repolarizare (la cele care prezinta histerezis). Pierderile prin conductie sint independente de frecventa. Energia pierduta prin repolarizare (dielectric cu caracter piezoelectric) este proportionala cu frecventa si cu aria ciclului de histerezis.
Parametrul care descrie raportul dintre componenta disipativa
si cea reactiva este ![]() .
.
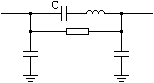
Elemente reactive parazite:
inductanta parazita (condensatoarele infasurate)
capacitati parazite intre terminale si masa.
Limite de functionare:
tensiunea instantanee (limitata de tensiunea de strapungere a dielectricului)
temperatura interna la functionare (pentru dielectricul cu disipatie importanta), limiteaza suplimentar tensiunea maxima, pentru ca temperatura interna depinde de puterea disipata si de temperatura externa
temperatura de depozitare
curentul instantaneu (in regim tranzitoriu)
Caracter neliniar: rar intilnit
Bobine
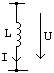
![]()
(In aceasta ecuatie au fost neglijate elementele reactive si disipative parazite si caracterul neliniar.)
Problema Cauchy:
![]()
![]() cunoscuta.
cunoscuta.
Solutia: 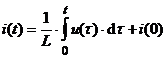
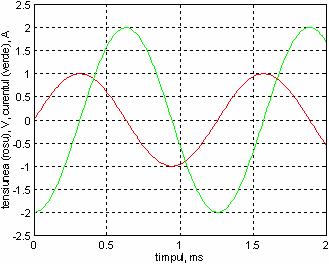
Daca i(t) este semnal sinusoidal, in regim permanent: ![]() .
.
Atunci tensiunea este: ![]() .
.
Cele doua marimi sint din nou de aceeasi forma dar, de data aceasta, se observa ca tensiunea este defazata in urma curentului cu un sfert de perioada.
In figura, semnal sinusoidal de perioada 1,25 ms (frecventa 800 Hz).
Modulul impedantei, ca raport intre amplitudinile tensiunii si curentului:
![]()
Reprezentarea in numere complexe:
![]()
Bobina inmagazineaza energie:
![]() (demonstratie asemanatoare cu
cea de la condensator).
(demonstratie asemanatoare cu
cea de la condensator).
Bobina ideala nu disipa energie. Bobina reala presupune si comportarea disipativa:
disipare in conductorul bobinei
disipare prin remagnetizare, la miezuri feromagnetice si ferimagnetice (proportionala cu aria ciclului de histerezis si cu frecventa)
disipare prin curenti turbionari, indusi in materialele conductoare din apropiere (cel mai adesea, in miezul metalic).
Parametrul care descrie raportul dintre componenta reactiva si cea disipativa este Q (factorul de calitate al bobinei).
Limite de functionare: curentul maxim admisibil, tensiunea maxima instantanee (in regim tranzitoriu), puterea maxima disipata.
Circuite pasive
Circuite rezistive
Valori limita pentru structurile serie si paralel
1. Puterea dispata maxima pentru un rezistor cu rezistenta R este P. Care sint tensiunea maxima si curentul maxim, presupunind regimul de curent continuu?
![]() , de unde
, de unde ![]() si
si ![]()
2. Puterea dispata maxima pentru un rezistor cu rezistenta R este P. Care sint tensiunea efectiva maxima si curentul efectiv maxim, presupunind regimul permanent sinusoidal?
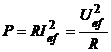 , de unde
, de unde ![]() si
si ![]() .
.
3. Doua rezistoare legate in serie au puterile disipate
maxime ![]() si
si ![]() .
Rezistentele lor sint
.
Rezistentele lor sint ![]() si
si ![]() .
Care este puterea maxima disipata a grupului?
.
Care este puterea maxima disipata a grupului?
Rezistoarele sint parcurse de
acelasi curent. Curentii maximi admisibili pentru rezistoare sint:  si
si 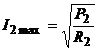 .
Curentul maxim admisibil al grupului este
.
Curentul maxim admisibil al grupului este ![]() .
Ca urmare, puterea maxima disipata a grupului este
.
Ca urmare, puterea maxima disipata a grupului este ![]() .
.
Exemplu: doua rezistoare de 1k si 2k, cu puterea disipata maxima de 200mW. Cel mai mic curent admisibil este cel prin rezistorul de 2k: 10mA. In total, puterea maxima disipata de cele doua rezistoare este de 300mW.
4. Doua rezistoare legate in paralel au puterile
disipate maxime ![]() si
si ![]() .
Rezistentele lor sint
.
Rezistentele lor sint ![]() si
si ![]() .
Care este puterea maxima disipata a grupului?
.
Care este puterea maxima disipata a grupului?
Tensiunea este aceeasi
pentru ambele rezistoare. Tensiunile maxime admisibile ale rezistoarelor sint: ![]() si
si ![]() .
Tensiunea maxima admisibila a grupului este
.
Tensiunea maxima admisibila a grupului este ![]() .
Ca urmare, puterea maxima disipata a grupului este
.
Ca urmare, puterea maxima disipata a grupului este 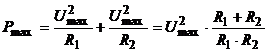 .
.
5. Doua condensatoare cu capacitatile ![]() si
si ![]() sint legate in paralel. Tensiunile maxime
admisibile sint
sint legate in paralel. Tensiunile maxime
admisibile sint ![]() si
si ![]() .
Care este tensiunea maxima admisibila a grupului?
.
Care este tensiunea maxima admisibila a grupului?
Tensiunea este aceeasi
pentru ambele condenstoare. Tensiunea maxima admisibila a grupului
este: ![]()
6. Doua condensatoare cu capacitatile ![]() si
si ![]() sint legate in serie. Tensiunile maxime
admisibile sint
sint legate in serie. Tensiunile maxime
admisibile sint ![]() si
si ![]() .
Care este tensiunea maxima admisibila a grupului?
.
Care este tensiunea maxima admisibila a grupului?
Ambele condensatoare
pastreaza aceeasi sarcina electrica. Sarcinile maxime
sint: ![]() si
si ![]() .
Sarcina maxima admisibila a grupului este
.
Sarcina maxima admisibila a grupului este ![]() .
Tensiunea maxima admisibila a grupului este:
.
Tensiunea maxima admisibila a grupului este: 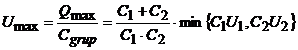 .
.
Exemplu: doua condensatoare de 10nF, cu tensiunile maxime de 50V, respectiv 250V. Tensiunea maxima admisibila este:
![]()
Problema propusa
Doua rezistoare conectate in paralel au parametrii: 10k si 0,5W, respectiv 15k si 0,25W. Se cer rezistenta echivalenta si puterea maxima disipata a grupului.
Divizoare de tensiune si curent, teoremele Thévenin si Norton
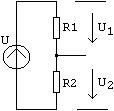
Pentru doua rezistoare legate in serie, tensiunile pe rezistoare sint:
![]() si
si ![]() .
.
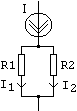
Similar, pentru divizorul de curent:
![]() si
si ![]() .
.
Valorile de mai sus presupun ca divizorul lucreaza in gol, adica nu mai exista alta sarcina conectata la divizor. In caz contrar, fie se fac calculele pe circuitul completat cu sarcina, fie (daca nu se cunoaste sarcina) se inlocuieste divizorul cu circuitul echivalat prin teorema Thévenin sau prin teorema Norton.
Proiectarea atenuatoarelor
Un atenuator este un circuit care diminueaza puterea semnalului. De regula, circuitele proiectate cu acest scop sint circuite pasive si sint calibrate (adica atenuarea este cunoscuta cu precizie).
Doua utilizari frecvente ale atenuatoarelor:
atenuatoare calibrate pentru intrarea in circuitele de masurare, asigura posibilitatea de a masura pe scari diferite, variabile in trepte. Sarcina atenuatorului este intrarea in circuitul de masura;
atenuatoare pentru iesirea din generatoarele de semnal, furnizeaza semnal la diferite valori ale nivelului. Atenuarea poate fi in trepte (atenuarea bruta, atenuatorul este calibrat) sau variabila continuu (brut + fin, atenuatorul nu mai pastreza caracterul de calibrat). Sarcina atenuatorului este circuitul catre care vrem sa dirijam semnalul generatorului.
Intr-o prima aproximatie, putem imagina atenuatorul compus numai din elemente rezistive, conectate in trepte succesive de divizare a tensiunii sau a curentului. Pentru ca atenuarea sa fie precisa, rezistoarele trebuie sa fie strict liniare si sa aiba eroare redusa.
Alegerea schemei depinde de modul in care se face comutarea treptelor:
conectarea sarcinii la trepte se face prin decuplarea unei portiuni de atenuator, ramasa nefolosita;
conectarea sarcinii la trepte se face fara decuplare de circuit.
Exemplul 1.
Atenuator cu mai multe trepte, comutate prin decuplarea celorlalte
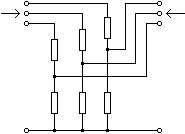
Exemplul 2.
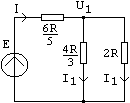
In convertoarele numeric/analogic (Digital to Analog Converters) se face divizarea tensiunii sau curentului de referinta in raportul 1:2:4:8:16:32:64:128:256:512:1024:2048. Pentru divizarea prin 2 se foloseste celula de divizare din figura (stinga):
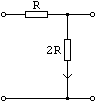
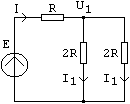
Proprietatile sale: Daca la stinga se monteaza o sursa de tensiune iar la dreapta se vede o rezistenta echivalenta 2R, atunci tensiunea este divizata prin 2 iar rezistenta echivalenta care se vede la bornele din stinga este tot 2R.
In figura de mai sus (dreapta),
![]() ;
;
![]() ;
;
![]() .
.
Prin conectarea in cascada a mai multor celule se alcatuieste reteaua R-2R. La dreapta fata de fiecare latura vericala se vede rezistenta echivalenta 2R. La dreapta fata de fiecare rezistor R se vede rezistenta echivalenta R.
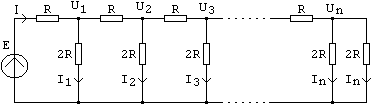
![]() ;
; ![]() ;
;
![]() ;
;
![]()
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Exemplul 3.
In atenuatoarele de intrare ale osciloscoapelor si ale altor aparate de masura, treptele de atenuare sint:
20V, 10V, 5V, 2V, 1V, 0,5V, 0,2V, 0,1V, 50mV, 20mV, 10mV, 5mV. Rapoartele de divizare corespunzatoare sint: 1:2:2:2,5:2:2:2,5:2:2:2,5
In acest scop se modifica sectiunile retelei de atenuare. Pentru divizare prin 2 se foloseste celula de divizare R-2R, prezentata mai sus. Pentru divizare prin 2,5 se foloseste o celula de divizare similara, la care se pun conditiile:
![]() (rezistenta
echivalenta a intrarii in celula este 2R, daca i se ataseaza la dreapta o sarcina 2R)
(rezistenta
echivalenta a intrarii in celula este 2R, daca i se ataseaza la dreapta o sarcina 2R)
![]() (raportul de
divizare), unde
(raportul de
divizare), unde ![]() .
.
Rezulta valorile: ![]() ,
,
![]() .
.
(Dupa acelasi model, se pot proiecta celule cu alte rapoarte de divizare.)
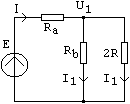
Prin combinarea celor doua tipuri de celula, se poate realiza reteaua cu rapoartele de divizare necesare aparatului de masura.

Diverse trepte de atenuare pot fi obtinute cu reteaua de mai sus, daca semnalul este cules din oricare nod, printr-un amplificator cu impedanta de intrare foarte mare. Pentru a evita aceasta conditie, se prefera utilizarea unui comutator multiplu care cupleaza amplificatorul numai la o sectiune a circuitului atenuator. Unul singur dintre comutatoare este cuplat in pozitia vericala, la un moment dat (dupa a doua celula, in figura de mai jos). Impedanta 2R din dreapta apartine intrarii in amplificator.

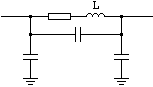
Pentru frecvente mari, capacitatile parazite ale componentelor determina atenuare variabila cu frecventa. Pentru a pastra acelasi raport de divizare, intr-un interval larg de frecventa, se introduc capacitati de compensare (vor fi exemplificate dupa capitolul dedicat comportarii in frecventa).
Problema propusa
Sa se proiecteze un atenuator cu trei trepte, de la tensiunea de intrare de 100V la 50V, 20V si 10V. Rezistenta de intrare trebuie sa fie de 1M. Sa se stabileasca cea mai mare putere disipata pe un rezistor.