|
|
|
Circuite logice elementare cu componente active
Acest tip de circuite logice contin si elemente active de circuit (tranzistoare) care, dupa cum se stie, sunt capabile sa amplifice un semnal.
1. Circuitul logic NU (NOT)
Circuitul
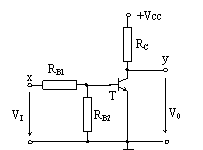
logic NU (NOT) are schema din fig. 5 si tabelul de adevar - tab. 3.
Tab. 3. Tabelul de adevar al
functiei NU (NOT)
x
y
0
1
1
0
Fig. 5. Circuitul logic NU (NOT)
Functionare: Cand x=0, VI=0V si borna de intrare a circuitului este conectata la masa, fig. 6a.
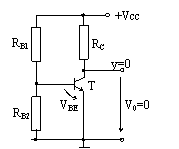
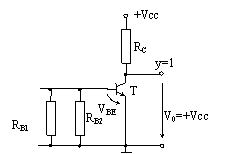
a) x=0 b) x=1
Fig. 6. Explicativa pentru intelegerea functionarii circuitului logic NU (NOT)
Baza tranzistorului este conectata la masa printr-o rezistenta echivalenta RB=RB1//RB2, deci VBE=0 si tranzistorul T este blocat. Potentialul +VCC se transfera la iesire prin Rc si V0=+VCC, deci y=1 logic.
Pentru x=1, VI=+VCC si ne aflam in situatia schemei echivalente din fig. 6 b. Divizorul RB1, RB2 este astfel dimensionat incat VBE≥0,7V, deci tranzistorul T este saturat si VCE=V0≈0,1V. Rezulta y=0 logic.
2. Circuitul logic SI-NU (NAND)
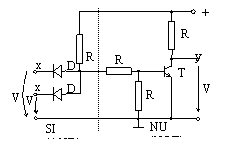
Circuitul logic SI-NU (NAND) prezinta schema din fig. 7, obtinuta prin conectarea in cascada a unui circuit SI (AND) pasiv si a unui circuit NU (NOT).
Tabelul de adevar, tab. 4, se
obtine din tab. 1. al functiei SI (AND), modificat in sensul
negarii valorilor logice din coloana functiei.
Tab. 4. Tabelul de adevar al
functiei SI-NU (NAND)
x2
x1
y
0
0
1
0
1
1
1
0
1
1
1
0
Fig. 7. Circuitul logic SI-NU (NAND)
3. Circuitul logic SAU-NU (NOR)
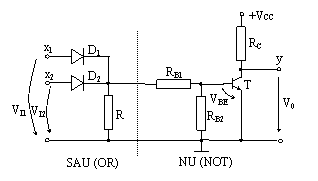
Circuitul logic SAU-NU (NOR), fig. 8, se obtine prin conectarea in cascada a circuitului SAU (OR) din fig. 3 cu circuitul NU (NOT) din fig. 5.
Tab. 5. Tabelul de adevar al
functiei SAU-NU (NOR)
x2
x1
y
0
0
1
0
1
0
1
0
0
1
1
0
Fig. 8. Circuitul logic SAU-NU (NOR)
Tabelul de adevar 5 se obtine din tab. 2 prin negarea valorilor logice din coloana functiei de iesire y.
