Indicatori ai sondajului aleator simplu

INDICATORI AI SONDAJULUI ALEATOR SIMPLU

GENERALITATI

Populatia statistica formata de obicei din obiecte sau indivizi supusa

cercetarii statistice, in  urma prelevarii celor n unitati statistice din cele N ale populatiei initiale conduce la formarea esantionului. Valorile caracteristice urmarite pentru cele n unitati sunt : x1, x2,,xn cu ajutorul carora definim media u.m., care difera mai mult sau mai putin de care este necunoscuta. Efectuand o alta esantionare din aceiasi populatie si determinand media valorilor inregistrate este foarte probabil ca aceasta sa difere de cea calculata anterior, ca urmare faptul ca indicatorii statistici calculati pe baza datelor de sondaj difera de la esantion la esantion, rezulta ca ei pot fi interpretati ca variabile aleatoare, din acest motiv prelucrarea datelor de sondajse face cu metode specifice disciplinei "probabilitati si statistica-matematica".

Conditia ca un estimator obtinut pe baza datelor de sondaj sa poata fi extins la intreaga populatie trebuie sa indeplineasca anumite conditii, specifice variabilelor aleatoare, adica sa fie o estimatie: nedeplasata (valoarea medie a indicatorului de sondaj, pentru un volum n finit, sa coincida cu parametrul din populatia generala); consistenta (indicatorul de sondaj sa convearga in probabilitate catre parametrul teoretic din populatia generala, atunci cand n ia valori mari); eficienta (sa aiba dispersie minima).

Valorile estimate pe baza datelor de sondaj sunt evaluari aproximative ale adevaratelor valori ale parametrilor necunoscuti din populatia generala. Valorile estimate sunt afectate de erori si ceea ce obtinem prin sondaj reprezinta un interval de incredere sau de estimare care acopera valoarea necunoscuta a parametrului din populatia generala, cu o probabilitate fixata de cercetator.

Consideram qinf si qsup cele doua extremitati ale intervalului de incredere, valori care se obtin pe baza datelor sondajului x1, x2,.,xn astfel incat cu o probabilitate P = 1 - a sa fie indeplinita relatia  P (qinf < q < qsup) = 1 - a. Probabilitatea P se numeste nivel de incredere, iar a este nivelul sau pragul de semnificatie si se fixeaza prin programul de cercetare.

Pentru P cele mai utilizate valori sunt 90%, 95%, 99%, 99,9% si le corespund 10%, 5%, 1%, 0,1% pentru a

Un rol important il prezinta lungimea intervalului de incredere. Daca eroarea de sondaj urmeaza legea normala, atunci erorile egale in valoare absoluta au probabilitati egale de aparitie pentru acelasi volum al esantionului si vom defini eroarea limita admisa ca fiind numarul notat si definit astfel : D qsup - qinf):2.

2.Indicatori ai sondajului aleator simplu repetat si nerepetat

Cazul sondajului repetat. Fie o selectie aleatoare de volum n din populatia generala de volum N , unde X1, X2,Xn sunt variabile aleatoare independente avand aceiasi repartitie ca si variabila X. Vom spune ca X1,X2,,Xn este o selectie asupra variabilei aleatoare X, iar x1,x2,,xn sunt valori de selectie. Populatia generala fata de caracteristica X are media M(X) = si dispersia D2(X)=s20. Avand N volumul colectivitatii generale, probabilitatea ca X1 sa ia valoarea concreta x1 este P(X=x1)=1/N, analog P(X=x2)=1/N, , P(X=xn)=1/N adica este asigurata stabilitatea repartitiei caracteristicii X colectivitatea generala, de unde rezulta independenta variabilelor de sondaj X1, X2,,Xn.

Definim media de sondaj , unde , si calculam deci tragem concluzia ca media de sondaj este un estimator nedeplasat al mediei a colectivitatii generale.

Calculam dispersia mediei de sondaj :

de unde abaterea medie de sondaj 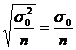adica dispersia mediei de sondaj intr-o esantionare cu intoarcere, de volum n este de n

ori mai mica decat dispersia a colectivitatii generale iar abaterea medie patratica a mediei de sondaj este de ori mai mica decat abaterea medie patratica a colectivitatii generale.

Folosind inegalitatea lui Cebasev se demonstreaza ca media de sondaj

(valoarea numerica a lui ) pentru un volum mare al esantionului converge in probabilitate catre media a populatiei, adica este un estimator consistent al mediei a populatiei.

Cazul sondajului nerepetat

Selectia in acest caz se face fara ca unitatea extrasa sa revina

in populatia generala, deci P(X1=x1)=1/N unde N este volumul populatiei initiale, dar P(X2=x2) este conditionata de faptul ca la prima extragere a avut loc evenimentul X1=x1 si unitatea nu revine in colectivitatea generala, asadar P(X2=x2/X=x1)=1/(N-1).

Vom demonstra ca daca X1,X2,,Xn este o selectie aleatoare din populatia generala ale carei elemente sunt de medie si dispersie , atunci:

si

Definim media populatiei generale astfel:

(1)

si dispersia populatiei generale:

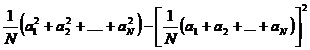= (2)

 (2')

Multimea tuturor selectiilor de volum n din populatia generala va contine  selectii :

(a1, a2, ..,an-1,an)

(a1, a2,..,an-1,an+1)

.

(a1, a2,an-1, aN)

.

(aN-n+1, aN-n+2,.aN-n+(n-1),aN-n+n) (3)

Toate selectiile sunt egal probabile, astfel incat probabilitatea de a obtine oricare din selectiile multimii definite de (3) este adica .

Presupunem ca selectiile din (3) au mediile .

Media mediilor de selectie este:

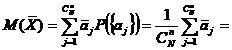
.  (4)

Selectiile din (3) care il contin pe a1 se obtin alegand alte (n-1) elemente din cele (N-1) elemente care mai contin populatia totala si aceasta se poate realiza in moduri. In urma acestei analize tragem concluzia ca in (4) elementul a1 intervine de ori, afirmatie care ramane valabila pentru oricare alt element ai, i=2, 3, ,N, deci (4) devine:

(5)

adica media mediei de selectie coincide cu media populatiei generale, deci este un estimator nedeplasat.

Definim dispersia mediei de selectie astfel:

(6)

Calculam momentul initial de ordinul doi al mediei de sondaj :

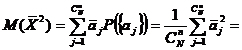
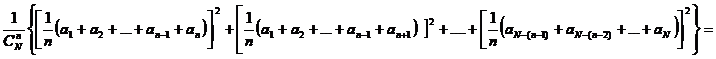
(7)

Printr-un rationament asemanator cu cel folosit la medie, se stabileste ca fiecare , i=1, 2, N apare de ori in (7) in timp ce ai si aj , ij, i,j=1, 2, ..N

Apar impreuna in selectii.

  (8)

Folosind (5) si (8) in (6), obtinem:

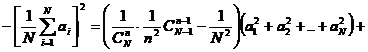
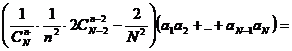
folosim relatia (2')=

Deci  (9)

Abaterea medie patratica in acest caz este :

  (10)