|
|
|
Data: 03.12.
Clasa: a X-a C
Profesor:
Disciplina: Matematica
Subiectul lectiei: Ecuații iraționale
Tipul lectiei: Lectie de comunicare/ insusire de noi cunostinte
Competente generale:
Reprezentarea adecvata a datelor cuprinse in enunturi matematice
Formarea deprinderii de utilizare a algoritmilor si a conceptelor matematice pentru caracterizarea locala a unei situatii concrete
Dezvoltarea capacitatilor de explorare/ investigare si rezolvare de probleme
Analiza unei situatii in scopul descoperirii de strategii pentru optimizarea solutiilor
Competente specifice:
Recunoasterea unei ecuatii irationale
Stabilirea conditiilor de existenta a radicalilor ce apar intr-o ecuatie irationala
Calcularea si verificarea solutiilor unei ecuatii irationale
Utilizarea unor strategii diferite de rezolvare in vederea optimizarii solutiilor
Prezentarea si justificarea intr-un mod explicit (coerent), folosind limbajul matematic adecvat, a metodei de rezolvare aplicate.
Strategia didactica
Metode si procedee folosite: conversatia, demonstratia, expunerea, invatarea prin descoperire, explicatia, exercitiul, exercitiul comentat, munca independenta, activitate frontala.
Mijloace de invatamant utilizate: manualul, culegere de probleme; C. Nastasescu, M.Brandiburu, C.Nita, D.Joita -Exercitii si probleme de algebra pentru clasele IX-XII, Ed. Didactica si Pedagogica, Bucuresti), fisa de lucru (Anexa)
Forme de organizare: frontal si individual
DESFASURAREA LECTIEI
ETAPELE
LECTIEI
CONTINUTUL LECTIEI
ACTIVITATI DE INVATARE
STRATEGIA DIDACTICA
EVALUARE
Moment organizatoric
Verificarea prezentei.
Asigurarea climatului adecvat si crearea unei stari psihologice favorabile desfasurarii lectiei.
Impartirea fiselor de lucru.
Frontal
Conversatia
Verificarea
continuturilor insusite
Actualizarea cunostintelor teoretice dobandite: existența radicalilor.
Rezolvarea exercitiului 1 cuprins in Fisa de lucru.
Pe parcursul desfasurarii activitatii se vor adresa elevilor intrebari ajutatoare/suplimentare, destinate clarificarii si eliminarii unor nelamuriri sau confuzii.
Plansa
Activitate frontala
Activitate individuala
Fisa de lucru
Conversatia
Explicatia
Exercitiul
comentat
Observarea sistematica a atentiei si implicarii in rezolvarea exercitiilor.
Aprecieri verbale referitoare la corectitudinea rezolvarilor de la tabla sau din caiete.
Precizarea titlului si a obiectivelor lectiei
Se informeaza elevii cu privire la tema lectiei ce urmeaza a fi predata: ,,Ecuatii irationale''
Se comunica elevilor, intr-o forma accesibila, obiectivele propuse, adica ceea ce trebuie sa stie la sfarsitul activitatii de predare.
Frontal
Expunerea
Comunicarea noilor cunostinte.
Dirijarea invatarii.
Def. Ecuatiile care contin necunoscuta sub semnul radical, se numesc ecuatii irationale.
Ex 
; 
; 
; 
; etc
Amintim ca radicalii de ordin par sunt definiti numai pentru numere nenegative, acestia fiind de asemenea numere nenegative.
Consideram exemplele:
1)
Cum radicalii de ordin 2 sunt definiti doar pentru numere nenegative, rezulta ca solutiile ecuatiei trebuie sa verifice sistemul de inecuatii:
x- 3
0; 2- x0 
x3 si x≤2 . Deci, sistemul de inecuatii nu
are solutii. Prin urmare, ecuatia 1) nu are solutii reale.
2) 
Cum 
si 
sunt nenegative,
avem suma+0, 
x
R. Membrul din dreapta ecuatiei este un numar
negativ -7<0, iar cel din stanga nenegativ, asadar ecuatia 2) nu
are solutii.
Obs Cele 2 exemple ne arata ca este necesar ca inainte de a trece la rezolvarea unei ecuatii irationale, prin diferite metode, sa ne asiguram ca solutiile acesteia pot exista.
METODE DE REZOLVARE A ECUATIILOR IRATIONALE
Calea obisnuita de rezolvare consta in eliminarea succesiva a radicalilor, prin diferite transformari, reducandu-le astfel la ecuatii deja studiate (de exemplu de gradul I sau II). Acest lucru se realizeaza prin ridicarea la o anumita putere a ambilor membri ai ecuatiei sau prin inmultire cu expresii conjugate.
EX.1. 
Pentru ca radicalul sa existe trebuie ca 2- x
0, de unde x≤2
Ridicam ambii membri ai ecuatiei la patrat si obtinem:
x2 = 2-x sau x2+ x - 2=0, rezulta x1= -2 si x2 =1
Desi ambele solutii sunt ≤2, inca nu putem
trage concluzia ca acestea sunt solutiile ecuatiei date,
deoarece la acelasi rezultat am fi ajuns si daca am fi considerat
ecuatia irationala 
. Trebuie sa verificam daca,
intr-adevar, valorile -2 si 1 sunt radacinile
ecuatiei date. Pentru x= -2, membrul stang este 
=2, iar cel drept -2. Deci, x= -2 nu este
radacina a ecuatiei considerate.
Elevii vor rezolva exercitiul 2 punctele de la a) pana la c) din fisa de lucru.
EX. 2. 
Punem conditiile de existenta a radicalilor:
5-x 0 si x 0, adica x ≤5 si x 0, rezulta x[0;5]
Se izoleaza un radical scriind ecuatia: 
- 
. Ridicam ambii membri la patrat:
5 -x= 9- 6+x 3=x+29x=x2+4x+4 x2
-5x+4=0 x
Facand verificarea constatam ca 1 si 4 sunt solutii ale ecuatiei date.
Elevii rezolva ecuatiile de la punctul 5) d, f, g
EX. 3. 
(*)
Din conditiile de existenta a radicalilor x 1
Se inmultesc ambii membri ai ecuatiei cu expresia conjugata a membrului stang. In urma calculelor se obtine:
(**)
Adunand membru cu membru ecuatiile (*) si (**)
x=2, care verifica ecuatia initiala.
Frontal
Expunerea
Frontal
Invatarea prin descoperire
Demonstratia
Explicatia
Conversatia
Activitate frontala si individuala
Exercitiul
Fisa de lucru
Explicatia
Demonstratia
Conversatia
Invatarea prin descoperire
Frontal sau individual
Fisa de lucru
Explicatia
Demonstratia
Conversatia
Frontal sau individual
Fisa de lucru
Explicatia
Demonstratia
Conversatia
Observarea sistematica
Aprecieri asupra gradului de implicare pe parcursul predarii.
Evidentierea
elevilor care au terminat primii si corect exercitiile.
Compararea rezultatelor obtinute.
Observarea sistematica a atentiei.
Aprecierea corectitudinii rezolvarilor. Optimizarea rezultatelor.
Asigurarea retentiei si a transferului
Se repeta cu elevii partea teoretica esentiala. Profesorul remarca din nou necesitatea de a verifica (in forma initiala a ecuatiei) daca radacinile gasite sunt intr-adevar solutii ale ecuatiei date, aceasta etapa facand parte din insasi rezolvarea ecuatiilor irationale.
Conform metodelor de rezolvare, aplicate si explicate de profesor ca model, elevii sunt solicitati sa rezolve ecuatiile irationale corespunzatoare din fisa de lucru, la tabla sau individual, in functie de nivelul de pregatire al colectivului de elevi, de capacitatea de intelegere si experienta anterioara.
Conversatia
Frontal
Exercitiul
Fisa de lucru
Aprecieri verbale si prin note a modului corect de rezolvare a ecuatiilor.
Tema pentru acasa
Ecuatiile ramase nerezolvate din fisa de lucru se vor da ca tema pentru acasa.
Se vor da indicatii de rezolvare, daca este cazul.
Conversatia
Explicatia
FISA DE LUCRU
R, pentru care exista urmatorii radicali: a) 
b) 
c)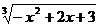 
a) 
b) 
c) 
d) 
e) 
f) 
g) 
h) 
i) 
j) 
k) 
l) 
