
|
|
|
PLAN DE LECTIE
Clasa: a XII-a C - M2
Tema: Matrice. Determinanti
Tipul lectiei: recapitulare si sistematizare de cunostinte
si determinanti;
-sa aplice aceste cunostinte in rezolvarea de exercitii.
lectiei
Activitatile din lectie necesare pentru realizarea obiectivelor
Strategia didactica
Captarea atentiei
Informarea elevilor asupra obiectivelor urmarite
Prezentarea materialului recapitulativ
Asigurarea retinerii si a transferului si a conexiunii inverse
Obtinerea de performanta
Asigurarea retinerii si a transferului si a conexiunii inverse.
Obtinere de performanta
Obtinere de performanta
Asigurarea retinerii si a transferului si a conexiunii inverse.
Profesorul pregateste clasa pentru ora.
Astazi vom rezolva exercitii cu matrice si determinanti.
1.Se
considera matricele I3 si A = 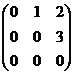 .
.
a) Sa se determine matricele A2 si A3.
b) Sa se determine matricea B = 6A5 - 3A2 +6I3.
c) Sa se calculeze determinantul matricei B.
2. In M2(IR),
multimea matricelor patratice de ordin doi peste IR, se
considera matricea A = ![]() .
.
a) Sa se calculeze A2.
b) Sa se determine matricele X ε M2(IR),
X = ![]() , astfel incat determinantul matricei (X + A) sa fie
egal cu 2.
, astfel incat determinantul matricei (X + A) sa fie
egal cu 2.
c) Sa se demonstreze ca pentru orice n natural nenul,
An = A.
d) Sa se demonstreze ca pentru orice n natural nenul,
A + 2A2 + . + nAn = ![]() .
.
3. Fie A = 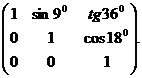 Sa se calculeze
determinantul si rangul matricei A.
Sa se calculeze
determinantul si rangul matricei A.
4. In M2(IR),
multimea matricelor patratice de ordin doi peste IR, se
considera matricea X(a) = ![]()
a) Sa se calculeze determinatul matricei X(a).
b) Pentru orice a, b reali, sa se arate ca X(a)·X(b) =
X(a + b + ab).
c) Sa se calculeze (X(1))2.
5. In M2(Q),
multimea matricelor patratice de ordin doi peste IQ, se
considera submultimea G = 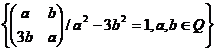
a)
Sa
se verifice ca I2 ![]() G
G
b)
Sa
se arate ca, daca A, B ![]() G, atunci AB
G, atunci AB![]() G;
G;
c)
Sa
se arate ca, daca X![]() G, X =
G, X = ![]() , atunci X este o matrice inversabila si ca
X-1 =
, atunci X este o matrice inversabila si ca
X-1 = ![]() ;
;
d)
Sa
se gaseasca o matrice A![]() G, cu b ≠ 0.
G, cu b ≠ 0.
6. Se
considera multimea G = 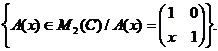
a) Sa se arate ca A(x)∙A(y) = A(x+y);
b) Sa se arate ca (G, ∙) este grup abelian.
c) Sa se rezolve in C ecuatia (A(x))2005 = A(1).
7. Sa se
rezolve ecuatia in C: 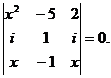
8. Sa se
rezolve ecuatia in C: 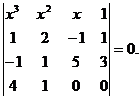
9.Sa se
calculeze determinatul 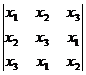 , unde x1, x2, x3 sunt
radacinile ecuatiei x3 - 2x2 + 2x + 17 = 0.
, unde x1, x2, x3 sunt
radacinile ecuatiei x3 - 2x2 + 2x + 17 = 0.
Tema pentru acasa: exercitiile ramase din fisa de lucru
Expunere
Explicatia
Elev la tabla
Exercitiu individual
Elev la tabla
Exercitiu frontal
Elev la tabla
Modelare logica
problematizare
Elev la tabla
Exercitiu frontal
Elevi la tabla
Descoperire prin analogie
Elevi la tabla
Problematizare
Exercitiu individual
Elev la tabla
1.Se considera matricele I3 si
A = 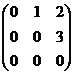 .
.
a)Sa se determine matricele A2 si A3.
b)Sa se determine matricea B = 6A5 - 3A2 +6I3.
c)Sa se calculeze determinantul matricei B.
2. In M2(IR), multimea matricelor
patratice de ordin doi peste IR, se considera matricea A = ![]() .
.
a)Sa se calculeze A2.
b)Sa se determine
matricele X ε M2(IR), X = ![]() , astfel incat determinantul matricei (X + A) = 2.
, astfel incat determinantul matricei (X + A) = 2.
c)Sa se demonstreze ca pentru orice n natural nenul, An = A.
d)Sa se demonstreze
ca pentru orice n natural nenul, A + 2A2 + . + nAn =
![]() .
.
3. Fie A = 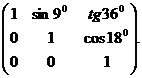 Sa se calculeze
determinantul si rangul matricei A.
Sa se calculeze
determinantul si rangul matricei A.
4. In M2(IR), multimea matricelor
patratice de ordin doi peste IR, se considera matricea X(a) = ![]()
a)Sa se calculeze determinatul matricei X(a).
b)Pentru orice a, b reali, sa se arate ca X(a)·X(b) = X(a + b + ab).
c)Sa se calculeze (X(1))2.
5. In M2(Q), multimea matricelor
patratice de ordin doi peste IQ, se considera submultimea G = 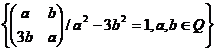
a)Sa se verifice ca
I2 ![]() G;
G;
b)Sa se arate
ca, daca A, B ![]() G, atunci AB
G, atunci AB![]() G;
G;
c)Sa se arate
ca, daca X![]() G, X =
G, X = ![]() , atunci X este o matrice inversabila si ca X-1
=
, atunci X este o matrice inversabila si ca X-1
= ![]() ;
;
d)Sa se
gaseasca o matrice A![]() G, cu b ≠ 0.
G, cu b ≠ 0.
6. Se considera multimea G = 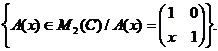
a)Sa se arate ca A(x)∙A(y) = A(x+y);
b)Sa se arate ca (G, ∙) este grup abelian.
c)Sa se rezolve in C ecuatia (A(x))2005 = A(1).
7. Sa se rezolve ecuatia in C: 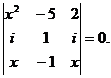 8. Sa se rezolve
ecuatia in C:
8. Sa se rezolve
ecuatia in C: 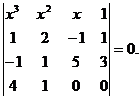
9.Sa se calculeze determinatul 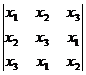 , unde x1, x2, x3 sunt
radacinile ecuatiei x3 - 2x2 + 2x + 17 = 0.
, unde x1, x2, x3 sunt
radacinile ecuatiei x3 - 2x2 + 2x + 17 = 0.