
|
|
|
Sistemul de scriere Egiptean
Egiptul a fost probabil prima civilizatie in care interesul pentru stiinte a fost major. Au excelat in medicina si matematici aplicate, dar si in astronomie, mecanica, chimie, fizica, administratie. Chiar numele de chimie provine de la alchimie, vechiul nume al Egiptului. Civilizatia Egiptului Antic a atins un inalt nivel inca din cele mai vechi timpuri. Datorita Nilului si climei, Egiptul avea tot ce-i necesar dezvoltarii unei civilizatii infloritoare. Egiptul era si usor de aparat avand o lunga granita cu desertul Sahara, asa ca s beneficiat de perioade lungi de pace, perioade in care societatea s-a dezvoltat rapid.
Cu 3.000 de ani i.C., in Egipt era dezvoltata puternic agricultura pe baza inundatiilor bianuale ale Nilului. Apa revarsata aducea aluviuni care imbogateau solul; surplusul de apa era dirijat printr-un sistem complicat de canale si ecluze, astfel ca ea sa fie folosita si in perioadele secetoase. Construirea si intretinerea unui astfel de sistem de irigatii a necesitat importante cunostinte de geometrie, mecanica, hidraulica. Cunoasterea cu precizie a perioadelor din an in care se produceau inundatiile era de maxima importanta. Problema a fost rezolvata de cunostintele avansate de astronomie care le-a permis realizarea unui calendar foarte precis. Teritoriul pe care se intindea Egiptul fiind vast, era nevoie de un sistem administrativ eficient. Pentru calcularea taxelor si repartizarea sumelor colectate pentru constructii, armata s.a. era nevoie de cunostinte de aritmetica. Din 3.000 i.C. a inceput constructia piramidelor; astfel marea piramida de la Ghiza a fost construita prin 2.650 i.C. Constructia piramidelor necesita vaste cunostinte si imense resurse materiale.
In acea perioada, Egiptenii aveau pus la punct sistemul de scriere hieroglific. Sistemul de numeratie folosit nu era foarte bun pentru realizarea calculelor aritmetice. Operatiile aritmetice, asa cum le cunoastem azi, erau foarte greu de realizat: adunarea si scaderea se puteau efectua relativ usor; inmultirea si impartirea erau de-a dreptul imposibile. Totusi, egiptenii au dezvoltat metode remarcabile pentru a trece peste acest neajuns.
La inceput, numerele erau sculptate in piatra pentru a comunica diferite marimi. Deoarece nu era nevoie sa se opereze mult cu ele, pentru cifre nu existau hieroglife speciale. Din momentul in care s-a trecut la utilizarea papirusului pentru scriere, a aparut necesitatea dezvoltarii unor mijloace mai rapide de scriere, a aparut necesitatea crearii unor hieroglife pentru scrierea numerelor.
Papirusurile descoperite arata ca egiptenii, spre deosebire de greci care s-au preocupat de studiul matematicii abstracte, erau legati de rezolvarea unor probleme de aritmetica legate exclusiv de practica.
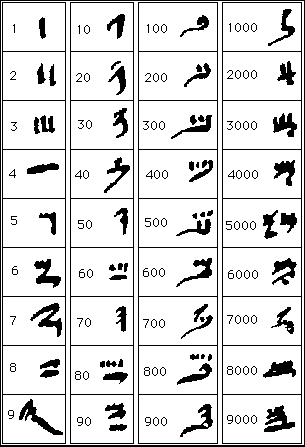
Sistemul de numeratie folosit de ei era zecimal si pozitional, dar nu in acceptia actuala. 'Cifrele' folosite se obtineau prin compunerea a sapte simboluri de baza:
![]()
1
un bat de masurat
![]()
10
un val
![]()
100
sfoara de masurat
![]()
1.000
floarea de lotus
![]()
10.000
degetul aratator
![]()
100.000
o broasca
![]()
1.000.000
un zeu cu mainile ridicate deasupra capului
Scrierea se facea in ordinea crescatoare a valorii. Iata cateva exemple:
3.244 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4
40
200
3.000
21.237 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
7
30
200
1.000
20.000
dar se putea scrie si pe verticala:
200
![]()
![]()
4.000
![]()
![]()
![]()
![]()
70
![]()
![]()
![]()
![]()
![]()
![]()
600
![]()
![]()
![]()
![]()
![]()
![]()
6
![]()
![]()
![]()
![]()
![]()
![]()
![]()
20
![]()
![]()
276
4
![]()
![]()
![]()
![]()
4.624
Deoarece se foloseau semne diferite pentru unitati, zeci, sute, mii, , nu are importanta ordinea scrierii. Nu era nevoie nici de simbol pentru zero.
![]()
Efectuarea unei inmultiri era destul de complicata. Sa consideram produsul 41 · 59. Construim o tabla astfel: randul 1 al doilea factor, 59, pe randurile urmatoare se scrie dublul randului precedent pana cand multiplicatorul devine mai mare ca primul factor, in cazul nostru pana la 32 < 41 < 64:
multiplicator
valoare
multiplicator
valoare
1
59
1
41
2
118
2
82
4
236
4
164
8
472
8
328
16
944
16
656
32
1.888
32
1.312
2.419
2.419
Apoi efectuam o serie de scaderi: 41 - 32 = 9; 9 - 8 = 1; 1 - 1 = 0 si scriem 41 = 32 + 8 + 1. Selectam multiplii corespunzatori si sumam.
Putem sa schimbam ordinea factorilor, 59 · 41. Avem 59 - 32 = 27; 27 - 16 = 11; 11 - 8
= 3; 3 - 2 = 1;
1 - 1 = 0. si scriem suma multiplilor 59 = 32 + 16 + 8 + 2 + 1.
Metoda folosita se bazeaza pe teorema care spune ca orice numar poate fi scris ca o suma a puterilor lui 2. Egiptenii nu aveau o dovada in acest sens si nici nu-i interesa s-o obtina. Stiau ca metoda este buna si o aplicau. Pur si simplu! Totusi, noi ne putem permite sa scriem:
41 = 1·20 + 0·21 + 0·22 + 1·23 + 0·24 + 1·25,
respectiv:
59 = 1·20 + 1·21 + 0·22 + 1·23 + 1·24 + 1·25.
![]()
Impartirea se realiza tot prin dublare. Sa luam, de exemplu, numarul 1.495 si sa-l impartim la 65. Construim un tabel ca la inmultire:
multiplicator
valoare
1
65
2
130
4
260
8
520
16
1.040
1.495
si ne oprim in momentul in care valoarea din tabel devine mai mare decat deimpartitul, adica la 1.040 < 1.495 < 2.080. Avem: 1.495 - 1.040 = 455; 455 - 260 = 195; 195 -130 = 65, 65 - 65 = 0, deci: 1.495 = 1.040 + 260 + 130 + 65.
Adunam multiplicatori corespunzatori: 1 + 2 + 4 + 16 = 23. Acesta este catul impartirii 1.495 : 65.
In exemplul de mai sus, 1.495 se divide cu 65. Cum se calculeaza in cazul in care deimpartitul nu se divide cu impartitorul? Sa consideram impartirea 1.500 : 65. Construim tabelul:
multiplicator
valoare
1
65
2
130
4
260
8
520
16
1.040
1.495
Si de data aceasta ne oprim in momentul in care valoarea din
tabel devine mai mare decat deimpartitul, adica la
1.040 < 1.500 < 2.080.
Adunam valorile n pentru care avem: 1.500 - 65 < n ![]() 1.500:
1.500:
1.040 + 260 + 130 + 65 = 1.465
Diferenta 1.500 - 1.465 = 5 reprezinta restul impartirii.
Sumam multiplicatorii corespunzatori: 1 + 2 + 4 + 16 = 23. Acesta este catul impartirii. Atunci se poate scrie:
1.500 : 65 = 23 + 5/65 = 23 1/13
![]()
Egiptenii foloseau numai fractii cu numaratorul 1, cu exceptia a doua fractii mai des folosite: 2/3 si 3/4. Iata cateva exemple:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1/3
1/25
1/269
Urmatoarea problema pe care ne-o punem este cum se efectueaza inmultirea si impartirea cu fractii. Sa luam ca impartitor fractia 1/5. Am fi tentati sa procedam ca mai sus, prin dublarea acesteia: 1/5 + 1/5. Din motive pe care nu le discutam, egiptenii, in loc sa efectueze acest calcul ar fi adunat 1/3 + 1/15. Papirusul Rhind contine o tabla care permitea dublarea unor fractii de tipul 1/n, pentru 5 < n < 101 impar, cu numaratorul 1. Iata inceputul acestei table:
Fractia
de dublat
Fractiile
care dubleaza
1/5
1/3 + 1/15
1/7
1/4 + 1/28
1/9
1/6 + 1/18
1/11
1/6 + 1/66
1/13
1/10 + 1/26 + 1/65
1/15
1/10 + 1/30
1/17
1/12 + 1/51 + 1/68
Este remarcabil de observat ca papirusul nu contine erori (apr cateva din copiere), ca termenii descompunerii sunt fractii cu numitori apropiati ca valoare si ca niciodata nu sunt mai multi de 4.
Cum rezolvau egiptenii ecuatia: 2/3 + 1/15 + x = 1 ?
Se multiplica cu 15: 10 + 1 + y = 15. Aceasta era numita auxiliar rosu, deoarece scribul folosea cerneala rosie la scrierea ei. Solutia ei este, evident, 4.
Pentru a obtine solutia ecuatiei initiale scriem:
dublu ´ (dublu ´ 1/15)
Din tabla de mai sus observam ca dublu ´ 1/15 este suma 1/10 + 1/30, pe care dubland-o se obtine 1/5 + 1/15, care este solutia ecuatiei date.
Iata si o problema: O cantitate adaugata la un sfert din cantitate da 15. Cat este cantitatea ?
Problema se transcrie in limbaj modern astfel:
x + x / 4 = 15
Presupunem ca x ar fi egal cu 4. Atunci x + x / 4 = 5, ceea ce nu este corect. Dar 15 este de 3 ori 5. Asa ca presupunerea trebuie multiplicata cu 3. Deci, raspunsul corect este x = 12.
Mai multe probleme din papirusul Rhind folosesc in rezolvare metoda falsei ipoteze (aplicata mai sus).
Cum procedau egiptenii pentru a rezolva calculul: (1 + 1/3 + 1/5) · (30 + 1/3) ? Foloseau metoda dublarii:
1
1 + 1/3 + 1/5
2
2 + 2/3 + 1/3 + 1/15 = 3 + 1/15
4
6 + 1/10 + 1/30
8
12 + 1/5 + 1/15
16
24 + 1/3 + 1/15 + 1/10 + 1/30
2/3
2/3 + 1/6 + 1/18 + 1/10 + 1/30
1/3
1/3 + 1/12 + 1/36 + 1/20 + 1/60
Penultima linie din tabel s-a obtinut astfel:
2/3 din 1 este 2/3;
2/3 din 1/3 este dublul lui 1/9 care este 1/6 + 1/18;
2/3 din 1/5 este dublul lui 1/15 care este 1/10 + 1/30.
Acum trebuie gasite numerele din prima coloana care insumate dau 30+1/3. Rezultatul se obtine sumand valorile din a doua coloana. Acesta este:
46 + 1/5 + 1/10 + 1/12 + 1/15 + 1/30 + 1/36.
O alta problema din papirusul Rhind: Un teren rotund are diametrul de 9 khet. Ce arie are ?
Solutia prezentata in papirus este urmatoarea:
Se afla 1/9 din diametru, adica 1; restul este 8. Inmultind 8 cu 8 ne da 64. Asa ca terenul are 64 setat.
1
9
1/9
1
1
9
2
16
4
32
8
64
De observat ca solutia este echivalenta cu p = 4(8/9)2 = 3.1605. Calculand acum, obtinem »3.160493 care difera de rezultatul obtinut de egipteni decat la a 4-a zecimala. Este un lucru remarcabil daca tinem cont de perioada in care a fost obtinut.
![]()
In papirusul din Moscova este prezentata urmatoarea problema, ilustrata in figura alaturata:
Problema cere sa se calculeze un trunchi de piramida pornind de la urmatoarele date: baza mare este un patrat cu latura de 4 cubit, baza mica este un patrat cu latura de 2 cubit si distanta dintre baze este de 6 cubit.
In primul rand trebuie remarcat ca prin sa se calculeze un trunchi de piramida se intelege sa se calculeze volumul unui trunchi de piramida.
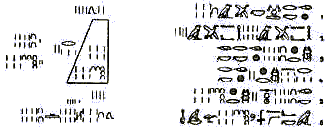
Calculul incepe cu aflarea ariei bazei mari: 4 · 4 = 16.
Se calculeaza apoi aria bazei mici: 2 · 2 = 4.
Se inmultesc latura bazei mari cu latura bazei mici: 4 · 2 = 8.
Se aduna rezultatele: 16 + 4 + 8 = 28.
Se calculeaza 1/3 din inaltime, adica: 2.
In final, se inmulteste ultimul rezultat cu suma calculata anterior si se obtine 56.
Aceasta problema arata ca egiptenii stiau formula volumului trunchiului de piramida. Astfel, luand a latura bazei mari, b latura bazei mici si h inaltimea, formula s-ar traduce in limbaj modern:
V = h/3 · (a2 + ab + b2)
![]()
Dupa inventarea scrierii pe papirus, egiptenii au creat 'cifrele' hieratice. Cu ajutorul lor, numerele puteau fi scrise intr-o maniera mult mai compacta. In noua scriere existau simboluri pentru 1,.., 9; 10, , 90; 100, , 900; 1.000, , 9.000.
De exemplu, numarul 9.999 se scria acum cu 4 hieroglife in loc de 36.
Iata un exemplu:
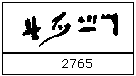
Cele doua sisteme de scriere au coexistat mai bine de 2.000 de ani. Cel hieratic era folosit pentru scrierea pe papirus, cel obisnuit continuand sa se utilizeze pentru inscriptii cioplite in piatra.
Grecesc
Pana prin secolul 3 i.C., aproape fiecare republica greceasca folosea un alt sistem de notare a numerelor. Apoi, schimburile comerciale tot mai intense au dus la adoptarea unui sistem de notare preluat de la fenicieni. Totusi, diferentele intre sistemele de numeratie nu erau majore, principalul lor rol fiind legat de tranzactiile economice.
Primul de care ne vom ocupa este sistemul acrofonic folosit in mileniul 1 i.C. (Acrofonic inseamna ca notatia unui numar se face prin prima litera a numelui sau). Sistemul mai este cunoscut si sub numele de Attica, dupa regiunea din jurul Atenei in care a fost folosit. Principalele simboluri folosite erau:
Numele
literei
Simbolul
literei
Numele
numarului
Valoarea
Iota
I
(iota)
1
Pi
G
(penta)
5
Delta
D
(deka)
10
Eta
H
(hekaton)
100
Chi
C
(chilioi)
1.000
Mu
M
(myrioi)
10.000
In afara de caracterul I - care este o abreviere - simbol intalnit in aproape toate sistemele pentru notarea numarului (cifrei) unu, celelalte simboluri deriva din fonograme. De exemplu, simbol G este o versiune mai veche a lui P (pi), prima litera a cuvantului Penta (penta), care inseamna cinci. La fel, simbolul D este delta, prima litera a cuvantului Deka (deca), ce inseamna zece; simbolul H este eta, prima litera a cuvantului Hekaton (hecaton), ce inseamna o suta.
Ca si cel egiptean sau cel roman, primul sistem de numeratie grecesc este unul aditiv. De exemplu, pentru a afla numarul:
DDGIII
se aduna valorile individuale:
DDGIII = 10 + 10 + 5 + 1 + 1 + 1 = 28
De observat ca nu are importanta ordinea in care sunt scrise simboluri din alcatuirea numarului. Totusi, era preferata scrierea simbolurilor in ordine descrescatoare a valorii acestora.
Pentru reprezentarea unor numere (mai ales a celor mari), este nevoie de foarte multe simboluri. De ex., pentru a scrie 9.999 se folosesc 32 de simboluri:
CCCCCCCCC HHHHHHHHH DDDDDDDDDGIIII
Nu este surprinzator ca apare un simbol pentru 5 de vreme ce baza de numeratie folosita este 10, provenind de la cele 10 degete, caci la o mana avem 5 degete. Este insa interesant ca vechii greci aveau simboluri pentru 50, 500, 5.000 si 50.000, simboluri care proveneau din combinatia simbolului pentru 5 cu simbolurile pentru 10, 100, 1.000, 10.000:
Simbolul
literei
Valoarea
![]()
50
![]()
500
![]()
5.000
![]()
50.000
Asa cum am spus si mai inainte, existau diferente intre reprezentarile caracterelor in diferite state. Iata cateva pentru 50:
![]()
Pentru vechii greci numarul nu era o notiune abstracta, era legat de obiectele pe care le numara. Astfel, pentru a preciza o suma de 5.678 de drahme ei scriau:
![]()
in care se observa ca simbolul unitatilor este caracteristic pentru drahma.
Ca sa reprezinte 3.807, taleri scriau:
![]()
Se observa ca pentru unitati se foloseste simbolul T de la Taler.
Suma de 3.807 drahme si 5 oboli (1 obol = 1/6 drahme) era reprezentata astfel:
![]()
![]()
Cel de-al doilea sistem de care ne ocupam, folosit de vechii greci, este sistemul alfabetic. In acest sistem numerele sunt reprezentate prin literele alfabetului. Acest mod de reprezentare a fost copiat de la fenicieni. De fapt, si alfabetul pentru scrierea cuvintelor fusese copiat de la ei.
Grecii aveau 24 de litere in alfabet. Au mai adaugat 3 litere scoase din uz (simbolurile pentru 6, 90 si 900: digamma, koppa si sampi):
1
A
a
(alpha)
10
I
i
(iota)
100
R
r
(rho)
2
B
b
(beta)
20
K
k
(kappa)
200
S
s
(sigma)
3
G
g
(gamma)
30
L
l
(lambda)
300
T
t
(tau)
4
D
d
(delta)
40
M
m
(mu)
400
U
u
(upsilon)
5
E
e
(epsilon)
50
N
n
(nu)
500
F
f
(phi)
6
![]()
![]()
(digamma)
60
X
x
(xi)
600
C
c
(chi)
7
Z
z
(zeta)
70
O
o
(omicron)
700
Y
y
(psi)
8
H
h
(eta)
80
P
p
(pi)
800
W
w
(omega)
9
Q
q
(theta)
90
![]()
![]()
(koppa)
900
![]()
![]()
(sampi)
Evident, sistemul este zecimal. Ca si sistemul acrofonic, cel alfabetic este unul aditiv. De exemplu:
FMB = 500 + 40 + 2 = 542
Uneori, pentru a le deosebi de literele alfabetului, deasupra acestor simboluri se trasa o bara.
Doar cu aceste simboluri puteau fi reprezentate doar numere mai mici ca 1.000. Pentru numerele cuprinse intre 1,000 si 9,999 au fost create simboluri compuse din simbolurile de baza carora li se atasa litera i (iota) fie in stanga-sus, fie in stanga-jos:
1.000
iA
iA
2.000
iB
iB
3.000
iG
iG
4.000
iD
iD
5.000
iE
iE
6.000
i![]()
i![]()
7.000
iZ
iZ
8.000
iH
iH
9.000
iQ
iQ
Pentru numere mai mari se scria deasupra literei M (de la Miriad) un numar cuprins intre 1 si 9.999, valoarea acestuia multiplicandu-se cu 10.000:
b
sla
= 20.000
= 3.210.000
De multe ori, in loc sa se scrie deasupra literei M, se scria in fata acesteia:
iZROEMiEWOE = 71.755.875
Acest sistem le permitea grecilor sa scrie toate numerele aparute in viata de zi cu zi. Numere ca 71.755.875 erau, evident, o raritate, iar numere mai mari nu aveau de unde sa apara.
O alta modalitate de a multiplica cu zece mii valoarea unui simbol era scrierea cu doua puncte deasupra simbolului respectiv. De exemplu:
![]()
![]()
Vechii greci foloseau si fractii. Notatia era ambigua si determinarea valorii depindea in cea mai mare masura de context. Un accent plasat dupa un grup de simboluri numerice transforma grupul in inversul acestuia:
b = 1/2, iar mg = 1/43 dar putea sa insemne si: mg = 401/3.
Spre deosebire de egipteni, grecii foloseau si fractii cu numarator mai mare ca 1:
napd = 51/84
Se observa ca numaratorul este precizat cu suprabarare.
![]()
Inmultirea se realiza folosind distributivitatea:
spz · b = (s + p + z) · b ® (200 + 80 + 7) · 2 = 400 + 160 + 14 = 500 + 70 + 4 ® fod
Interesant este ca vechii greci efectuau impartirea in acelasi mod cum o efectuam si noi azi.
Roman
Inaintea romanilor, cea mai dezvoltata civilizatie din peninsula Italica a fost cea a etruscilor. Etruscii au copiat sistemul grecesc de numeratie acrofonic. Romanii au copiat sistemul de la etrusci si l-au adaptat alfabetului lor.
I
V
X
L
C
D
M
1
5
10
50
100
500
1.000
Sistemul de numeratie roman nu este un simplu sistem aditiv, ci unul aditiv-subtractiv.
La inceput, cifrele V, L si D lipseau.
1
I
un bat vertical
10
X
doua bete incrucisate
100
C
initiala cuvantului centum (100)
1.000
M
initiala cuvantului mille (1.000)
Pentru 1.000, romanii foloseau initial o alta
notatie: ![]() . Pe
10.000 il notau
. Pe
10.000 il notau ![]() , iar
pe 100.000 cu
, iar
pe 100.000 cu ![]() .
.
Regulile de scriere (preluate tot de la etrusci) erau:
Orice semn pus la dreapta altuia de valoare mai mare sau egala decat a lui, se aduna.
Exemplu:
XX = 10 + 10 = 20
XII = 10 + 1 + 1 = 12
Orice semn pus la stanga altuia de valoare mai mare decat a lui, se scade.
Exemplu:
IX = 10 - 1 = 9
IXC = 100 - (10 - 1) = 100 - 9 = 91
XCII = 100 - 10 + 1 + 1 = 100 - 10 + 1 + 1 = 92
Un punct de vedere propriu: Celelalte cifre romane cunoscute au aparut din nevoia de
simplificare a scrierii. Interesant este ca, spre deosebire de sistemul
grecesc, noile simboluri sunt si din punct de vedere grafic
jumatati ale unitatilor din care provin. Simbolul X =
10, daca este taiat in doua pe linia mediana
orizontala genereaza doua litere V (din care una
rasturnata) avand fiecare valoarea 5; in mod analog, taindu-l pe
C = 100 (sa nu uitam ca forma sa cioplita nu era
rotunjita, aratand astfel ![]() ) se obtin
doua litere L (din care una este rasturnata), fiecare cu
valoarea 50; taind pe linia mediana verticala pe
) se obtin
doua litere L (din care una este rasturnata), fiecare cu
valoarea 50; taind pe linia mediana verticala pe ![]() , vechiul simbol
pentru 1.000, se obtin doua simboluri
, vechiul simbol
pentru 1.000, se obtin doua simboluri ![]() , foarte
apropiat de litera D (din care una in oglinda), fiecare avand valoarea
500.
, foarte
apropiat de litera D (din care una in oglinda), fiecare avand valoarea
500.
Sistemul de numeratie roman este foarte greu de folosit, in
special la scrierea numerelor mari. Ca fapt divers: consemnarea numarului
de prizonieri in urma luptei cu cartaginezii, estimat la 2.300.000, s-a
facut prin repetarea semnului ![]() de 23 de ori !
de 23 de ori !
Dar chiar in cazul numerelor mici scrierea poate fi destul de complicata. De exemplu, numarul 879:
879 = 800 + 70 + 9 ® DCCCLXXIX
O alta lacuna a acestui sistem de numeratie este ambiguitatea regulilor de scriere. Astfel, numarul 8 poate fi scris fie ca VIII, fie ca IIX.
In vechiul sistem de numeratie roman (1.200 i.C.), cand au fost introduse formele substractive (ca IV = 4 sau IX = 9), era posibil sa se reprezinte orice numar mai mic decat 5.000 cu ajutorul unei serii de simboluri in care oricare nu aparea mai mult de 4 ori. De exemplu, 2.976 = MMDCCCCLXXVI.
Sistemul aditiv este foarte usor de folosit in calcule simple.
Adunarea se face in doi pasi: mai intai se scriu impreuna toate simbolurile din care sunt alcatuite cele doua numere, apoi se 'colecteaza' simbolurile de cea mai mica valoare si se inlocuiesc, daca este cazul, cu simboluri de valoare superioara:
2319+
MMCCCXIX
821
DCCCXXI
3140
MMDCCCCCCXXXIXI
MMDCCCCCCXXXX
MMDDCXL
MMMCXL
Inmultirea se face ceva mai greu:
28·
XXVIII
12
XII
56
XXVIII
ori
I
egal
XXVIII
28
XXVIII
ori
I
egal
XXVIII
336
XXVIII
ori
X
egal
CCLXXX
CCLXXXXXXXVVIIIIII
CCLXXXXXXXVVVI
CCLXXXXXXXXVI
CCLLXXXVI
CCCXXXVI
Scaderea si impartirea sunt ceva mai complicate, dar pot fi efectuate.
Zecimal
Este cel mai raspandit sistem de numeratie. Cifrele folosite in sistemul zecimal se numesc cifre zecimale. Asadar, cifrele sistemului zecimal sunt numerele naturale mai mici ca 10 si se noteaza in ordine, respectiv cu:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Secventa de cifre zecimale 192544, sau mai precis 192544(10) reprezinta numarul natural:
1·105 + 9·104 + 2·103 + 5·102 + 4·101 + 4·100