
|
|
|
STUDIUL STABILITATII CADRELOR METALICE PORTAL - HALA METALICA
1 Instabilitatea in planul cadrului
Pentru a intelege mai bine conceptul de instabilitate al cadrului in planul sau, este nevoie a se avea in vedere doua efecte primare in ceia ce priveste comportarea structurii. Primul dintre acestea este reprezentat de efectele de ordinul doi, al doilea fiind considerat cel al instabilitatii.
Efectele de ordinul doi
Efectele de ordinul doi, in forma lor simplificata, se datoreaza in primul rand deplasarii laterale a cadrului in planul sau. Aceasta deplasare va cauza excentricitati ale fortelor verticale, care vor genera in cele din urma momente de ordinul doi datorita fortei axiale aplicate excentric in elementele verticale. Aceste momente de ordinul doi in literatura de specialitate sunt cunoscute sub numele de efectele P-Δ ("P" forta axiala aplicata la excentricitatea Δ) (Figura 1). Aceste momente pot avea o importanta ridicata in proiectarea in domeniul plastic a cadrelor metalice portal, in cazurile in care elementele sunt relativ zvelte, rezultatul verificarii luand in considerare aceste momente pot conduce la marirea sectiunilor transversale.

Figura 1 Efectele P-Δ asupra cadrelor portal
Doua concepte importante trebuiesc avute in vedere si anume:
Efectele P-Δ, se datoreaza nu numai incarcarilor orizontale,cat si urmatoarelor efecte:
- asimetria structurii;
- asimetria incarcarilor;
- lipsa verticalitatii stalpilor;
Efectele P-Δ nu cauzeaza neaparat instabilitatea cadrului. Ceia ce este necesar in acest caz, este o metoda pentru a determina daca efectele P-Δ sunt importante sau nu, si daca acestea vor cauza instabilitatea cadrului.
Instabilitatea
Conceptul de instabilitate poate fi foarte bine inteles, prin considerarea unei console verticale incarcate cu o forta axiala (Figura 2)
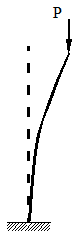
Figura 2 Instabilitatea unei console verticale
La forte axiale relativ reduse si/sau zvelteti mici ale consolei, orice forta disturbatoare va cauza deformarea consolei cu o valoare finita, iar in momentul in care aceasta perturbatie este indepartata, consola va reveni la forma ei initiala. La valori ridicate ale fortei axiale , chiar si cea mai mica forta disturbatoare, va cauza deformarea incontrolabila a barei, datorita efectelor de ordinul doi. Forta care cauzeaza instabilitate, este cunoscuta sub numele de forta elastica critica, iar raportul dintre aceasta si forta de exploatare care actioneaza asupra barei este demunit factorul elastic critic, λcr :
![]()
In normele in vigoare este specificat ca o
valoare ![]() inseamna ca
efectele de ordinul II sunt nesemnificante si pot fi neglijate.
inseamna ca
efectele de ordinul II sunt nesemnificante si pot fi neglijate.
O valoare ![]() , in mode general indica o structura potential
nestabila, caz in care o analiza de ordinul doi este necesar a fi
efectuata. Aceleasi efecte pot aparea si in cazul cadrelor
metalice portal, in consecinta orice forta orizontala
disturbatoare trebuie luata in considerare, pentru a putea realiza o
interpretare si o judecata a fenomenului de instabilitate. In mod
normal elementele cadrului au imperfectiuni initiale, generate de
procesul de productie sau de montajul structurii, acesta este un alt
aspect care poate genera instabilitate, fara luarea in considerare a
unei forte orizontale.
, in mode general indica o structura potential
nestabila, caz in care o analiza de ordinul doi este necesar a fi
efectuata. Aceleasi efecte pot aparea si in cazul cadrelor
metalice portal, in consecinta orice forta orizontala
disturbatoare trebuie luata in considerare, pentru a putea realiza o
interpretare si o judecata a fenomenului de instabilitate. In mod
normal elementele cadrului au imperfectiuni initiale, generate de
procesul de productie sau de montajul structurii, acesta este un alt
aspect care poate genera instabilitate, fara luarea in considerare a
unei forte orizontale.
Instabilitatea in-afara planului cadrului este verificata, tinandu-se cont de lungimea efectiva a elementelor individuale, intre punctele de prinderi laterale. Acesta este o metoda simplificata de proiectare a unei structuri simple, tinandu-se cont de comportarea structurii pe directie longitudinala. Oricum in planul cadrului rezistenta la deplasarea laterala, este conferita de rigiditatea elementelor si a imbinarilor, din acest motiv sunt necesare prevederi, care sa tina cont si de legarea cadrului pe directie longitudinala nu numai prin intermediul riglelor de perete si al panelor de acoperis, dar si prin contravantuirile din peretii longitudinali si din acoperis.
Cadrele metalice portal pot ceda fie prin pierdea stabilitatii generale, sau prin pierderea stabilitatii locale. Pierderea stabilitatii locale se poate datora flambajului lateral prin incovoiere rasucire a riglei cadrului, sau in unele cazuri a stalpului.
Pentru a urmarii stabilitatea cadrelor metalice portal cu rigla acoperisului inclinata, s-au analizat mai multe cadre avand aceiasi inaltime si deschidere, pante ale acoperisului diferite, si de asemenea prinderi la baza stalpului diferite. Inainte de a trece la analiza propriu zisa, s-a realizat calibrarea lor pe baza unor teste experimentale.
2 Cadrele studiate si modul de analizare
Au fost studiate un numar de cadre portal, avand aceiasi inaltime la streasina, cu unghiuri de acoperis diferite (10%, 20%) diferite moduri de prindere a stalpului la baza (Figura 3). Toate cadrele au rigla vutata si stalpi cu sectiune constanta sau variabila dupa caz (Figura 4).
|
|
|
|
|
(a) articulat |
(b) semi-rigid |
(c) rigid |
Figura 3: Prinderea stalpului la baza
|
|
|
|
(a) stalp variabil (var) |
(b) stalp constant (con) |
Figura. 4: Tipuri de cadre portal
Cadrele notate "var", au stalpi cu sectiune variabila de Clasa 1 pana la Clasa 3, iar cele notate "con" au stalpi cu sectiune constanta de Clasa 1. Sectiunea riglelor este de Clasa 1 pana la Clasa 3. Dimensiunile principale ale cadrelor sunt prezentate in Tabelul 1. Otelul utilizat este S235.
Analizele efectuate sunt: 3D statica elasto-plastica si 3D de flambaj. Analizele spatiale au fost efectuate cu programul ANSYS v5.4 iar elementele au fost modelate cu elemente de tip SHELL43 plastice. Comportarea materialului a fost considerate elastica-perfect plastica. In analizele 3D, au fost considerate blocaje laterale ale riglei introduse de pane [1]. Blocajele laterale sunt de 4 tipuri ( Figura 1) si anume: tipul 1 - fara blocaje laterale, tipul 2 - blocarea deplasarii laterale, tipul 3 - blocarea deplasarii laterale cat si a rotirii, tipul 4 - blocarea deplasarii laterale dar si a deplasarii laterale a talpii comprimate (in punctele in care se dispun contrafise).
|
|
|
|
|
|
(a) tip 1 |
(b) tip 2 |
(c) tip 3 |
(d) tip 4 |
Figura 5: Tipuri de blocaje laterale
Tabelul 1: Dimensiuni principale
|
Nr. |
Code |
Tip cadru |
LxH |
Prinderea la baza |
α |
Rigla |
Stalp |
|
|
constanta |
variabila |
|||||||
|
1 |
1C-1 |
var |
12x4.8 |
pin |
10% |
h=270 b=135 tf=10 tw=5 |
h=270600 b=135 tf=10 tw=6 |
h=240600 b=180 tf=12 tw=8 |
|
2 |
1C-1 |
var |
12x4.8 |
sem |
10% |
|||
|
3 |
1C-2 |
var |
12x4.8 |
pin |
20% |
|||
|
4 |
1C-2 |
var |
12x4.8 |
sem |
20% |
|||
|
5 |
3C-1 |
con |
12x4.8 |
sem |
10% |
h=270 b=135 tf=10 tw=5 |
h=270600 b=135 tf=10 tw=6 |
h=400 b=180 tf=12 tw=8 |
|
6 |
3C-1 |
con |
12x4.8 |
rig |
10% |
|||
|
7 |
3C-2 |
con |
12x4.8 |
sem |
20% |
|||
|
8 |
3C-2 |
con |
12x4.8 |
rig |
20% |
|||
Imbinarea rigla-stalp este rigida si este prezentata in Figura 4. Imbinarea rigla-stalp si prinderea stalpului la baza au fost modelate cu elemente de contact.
Incarcarile verticale permanente si din zapada au fost introduse in punctele de rezemare a panelor. O forta orizontala la coltul cadrului a fost considerata ca 12% din cele verticale. De asemenea in calcul au fost considerate si imperfectiuni initiale de inclinare si incovoiere.
Calibrarea modelelor
Modelele spatiale au fost calibrate pe baza unor rezultate experimentale, obtinute de Halasz si Ivany. Geometria, dimensiunile sectiunilor, detaliu de baza a cadrelor testate sunt prezentate in Tabelul 1.
3 Analiza de stabilitate.
Pentru cadrele portal, deoarece in rigla se dezvolta eforturi axiale semnificate, problema stabilitatii este mult mai complexa decat in cazul cadrelor multietajate [4]. Dupa cum bine este cunoscut, elementele acestor cadre isi pot pierde stabilitatea prin flambaj cu incovoiere-rasucire. In conformitate cu EC3 (EN 1993-1-1) , elementele cu sectiuni de Clasa 1 si Clasa 2, pentru care flambajul prin incovoiere-rasucire ar putea fi un mod de cedare, trebuie sa verifice:
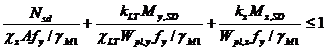
Elementele cu sectiuni de Clasa 3 solicitate la compresiune cu incovoiere, trebuie sa verifice urmatoarea relatie:
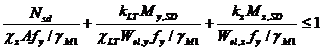
Pentru a observa comportarea cadrelor metalice considerate, acestea au fost supuse unor analize neliniare elasto-plastice, analize realizate cu programul ANSYS. In cadrul acestor analize au fost considerate blocaje de tipul 2 (Fig. 5). Mecanismul de cedare difera intre cele doua tipuri de cadre, instabilitatea se produce dupa cum urmeaza: flambaj lateral prin incovoiere-rasucire a riglei , cadre "var", flambaj prin incovoiere-rasucire a riglei si stalpului in cazul cadrelor de tip "con"
|
|
|
|
(a) var |
(b) con |
Figura. 6: Instabilitatea locala a elementelor
Comparatia intre rezultatele analizelor numerice si prevederilor in prEN1993-1-1 [5] pentru elemente de Clasa 3, avand talpa superioara blocata lateral sun prezentate in tabelul urmator:
Tabelul 2: Rezultate comparative intre analiza cu MEF si norme
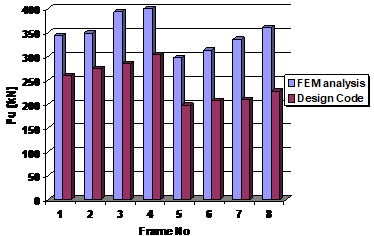
Cadru
Nr.
Fu [kN]
Analiza MEF
Norme
1
344
260
2
349
275
3
394
285
4
402
303
5
297
198
6
313
208
7
336
210
8
361
227
Rezultatele demonstreaza influenta pe care o au modul de prindere a stalpului la baza si unghiul de acoperis la capacitatea ultima a cadrului.
Comportarea cadrului sub efectul fortelor aplicate poate fi studiata si prin intermediul unor analize de flambaj, rezultand in acelasi timp si modul de flambaj al cadrului. Aceste analize au fost facute cu programul Ansys, v.5.4, rezultand comportamentul spatial al cadrului. In aceste analize au fost considerate blocajele laterale din Figura 5. Forta critica elastica pentru fiecare caz in parte (tip cadru, tip prindere laterala) sun trasate in Figura 7.
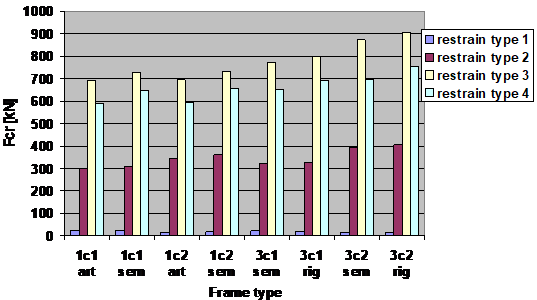
Figura 7: Valorile fortelor critice in functie de tipul de blocaj lateral
S-a observat ca modul de flambaj si valorile fortelor critice depind de tipul de prindere laterala a cadrului. Modurile proprii de flambaj sunt prezentate in Figura 8 pentru diferite tipuri de prindere: tipul 1 - flambaj lateral al riglei la valori relativ scazute ale fortei critice (Figura 8 a), tipul 2 - flambaj prin incovoiere-rasucire a riglei si stalpului, forta critica creste substantial (Figura 8 b); tipul 3 - flambaj prin incovoiere-rasucire a riglei si a stalpului, valoarea fortei critice creste de aproximativ trei ori fata de cazul precedent (Figura 8 c); tipul 4 - flambaj prin incovoiere-rasucire a riglei si stalpului (Figura 8 d), lungimea de flambaj a riglei fiind redusa datorita unui blocaj lateral suplimentar la talpa comprimata inregistrandu-se o crestere a fortei critice fata de cazul S-a observat de asemenea ca modul de flambaj este similar pentru cele doua tipuri de cadre (stalp cu sectiune constanta sau variabila).
a) prindere de tip 1

b) prindere de tip 2

c) prindere de tip 3

d) prindere de tip 4
Figura 8: Forme de flambaj
Din ultimele figuri se poate observa importanta blocajelor laterale pentru imbunatatirea rezistenta la flambaj a cadrelor.
4 Cazuri practice de proiectare
Rezultatele prezentate in paragrafele anterioare se refera la un numar de cadre calibrate, avand diferite solutii de prindere a stalpului la baza si diferite blocaje laterale. In continuare vor fi analizate cateva cadre parter. Cadrele selectate sunt des intalnite in proiectarea curenta a halelor metalice, avand stalpi articulati in fundatie, cu sectiune variabila, rigle vutate, si un unghi de acoperis de 80 (Figura 9). Lungimea vutei este de 0.15*L. Dimensiunile si caracteristicile sunt date in Tabelul 3.
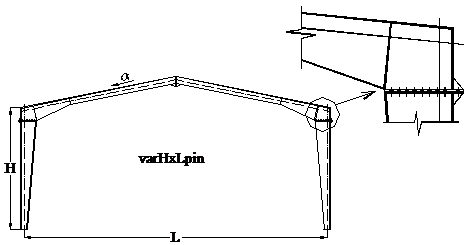
Figura 9: Geometria cadrelor analizate
Tabelul 3: Dimensiunile principale ale sectiunilor
|
Tip cadru |
H [m] |
L [m] |
Dimensiuni h*b*tf*tw [mm] |
||
|
stalp |
Vuta-rigla |
Rigla constanta |
|||
|
var4x18pin |
4 |
18 |
(350.800)*220*12*10 |
(400.800)*200*12*10 |
400*200*10*8 |
|
var4x24pin |
4 |
24 |
(450.900)*280*15*10 |
(500.900)*250*15*12 |
500*250*12*10 |
|
var4x30pin |
4 |
30 |
(500.1200)*350*15*12 |
(550.1200)*300*15*12 |
550*300*15*10 |
|
var6x18pin |
6 |
18 |
(350.800)*220*12*10 |
(400.800)*200*12*10 |
400*200*10*8 |
|
var6x24pin |
6 |
24 |
(450.900)*280*15*10 |
(500.900)*250*15*12 |
500*250*12*10 |
|
var6x30pin |
6 |
30 |
(500.1200)*350*15*12 |
(550.1200)*300*15*12 |
550*300*15*10 |
|
var8x18pin |
8 |
18 |
(350.800)*220*12*10 |
(400.800)*200*12*10 |
400*200*10*8 |
|
var8x24pin |
8 |
24 |
(450.900)*280*15*10 |
(500.900)*250*15*12 |
500*250*12*10 |
|
var8x30pin |
8 |
30 |
(500.1200)*350*15*12 |
(550.1200)*300*15*12 |
550*300*15*10 |
Cadrele au fost supuse unor analize elasto-palstice 3D cu programul de element finite Ansys v.5.4. Toate cadrele au fost modelate cu elemente de tip shell. In cadrul analizelor au fost aplicate blocaje laterale de tip 2 (vezi Fig. 5). Otelul utilizat fiind S235. Din Tabelul 3 se poate observa ca pentru aceiasi deschidere si inaltime diferita a cadrului a fost pastrata aceiasi sectiune de element.
O comparatie intre rezultatele obtinute si normele de proiectare este prezentata in Tabelul 4. Se observa ca fortele ultime obtinute in urma analizelor neliniare el-plastice (mult mai apropiate de cazul real) sunt superioare celor rezultate aplicand formulele din norme.
De asemenea crescand inaltimea structurii, forta ultima scade, aceasta poate fi explicata de rolul pe care stalpul il joaca in comportarea globala a cadrului.
Mai mult, nici in aceste cazuri nu a fost inregistrata o instabilitate globala, ci una locala. Mecanismul de cedare fiind flambaj prin incovoiere-rasucire a riglei sau a stalpului, depinzand de inaltimea cadrului (Figura 10).
Tabelul 4: Rezultate comparative MEF si Norme
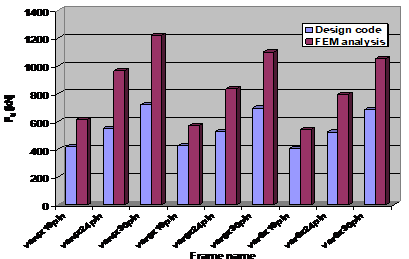
Denumire cadru
Fu [kN]
Analiza MEF
Norma
var4x18pin
615
418
var4x24pin
967
551
var4x30pin
1220
720
var6x18pin
569
426
var6x24pin
836
527
var6x30pin
1100
696
var8x18pin
544
407
var8x24pin
796
523
var8x30pin
1050
684
|
|
|
|
a) H=4 m |
b) H=6 m |
|
|
|
|
c) H=8 m |
|
Figura. 10: Moduri de cedare