placi plane

Consideratii generale

Placile sunt corpuri ce au o dimensiune, grosimea orientata dupa axa z, mult mai mica in raport cu celelalte doua (§I.3.1). Acest capitol trateaza cateva probleme simple din domeniul placilor considerate subtiri ce pot prelua solicitarea de incovoiere datorata actiunii fortelor orientate dupa axa z, perpendiculare pe planul median. Aceste placi indeplinesc conditia , unde l, de regula orientat dupa x, este latura mica a placii dreptunghiulare (cealalta latura) iar in cazul placii circulare se face referire la raza R a acestora.

Deformarea placii se evidentiaza din studiul curbarii planului median prin legi de variatie a sagetii w  si a rotirii ; se face abstractie de extinderea suprafetei mediane ca urmare a solicitarii acesteia.

Ipotezele de calcul din studiul barelor se admit in continuare iar unele se extind la calculul placilor. Se considera ca materialul placii este omogen, izotrop si legea generalizata a lui Hooke in domeniul elastic este satisfacuta. Se adopta o grosime a placii constanta.

Ipoteza lui Bernoulli devine ipoteza lui Kirchoff. Prin aceasta se admite ca punctele aflate pe normala la suprafata mediana raman pe normala la suprafata deformata. Se neglijeaza astfel lunecarile din material comparativ cu rotirea normalei. Inseamna ca punctele materiale ale placii se deplaseaza dupa normalele in planul median, in felul acesta fiind suficient studiul deformarii planului median. Deformatiile fiind mici comparativ cu dimensiuinile placii, se pot scrie intr-o prima etapa ecuatiile de echilibru pentru forma nedeformata. Se observa ca eforturile, si in consecinta tensiunile, nu mai pot fi determinate prin metoda sectiunilor. Se constata ca deformatiile, tensiunile si eforturile pot fi exprimate printr-o functie a rotirii j sau a deplasarii w. Problema consta in a stabili expresia uneia din aceste functii in baza studiului geometric, fizic si mecanic al placii.

Studiul placilor plane circulare incarcate simetric

1 Studiul geometric

Se considera cazul simplu al unei placi circulare simplu rezemata pe contur, articulata sau incastrata, definita intr-un sistem de referinta cilindric, incarcata simetric cu o sarcina uniform distribuita. Datorita simetriei, pe un cerc de raza oarecare, eforturile sunt aceleasi, dezvoltarea tensiunii avand o variatie identica indiferent de orientarea razei . Pentru studiu se izoleaza un volum elementar avand punctul M situat la o raza de centrul placii si la o distanta fata de planul median. Suprafetele volumului elementar sunt:, ,.

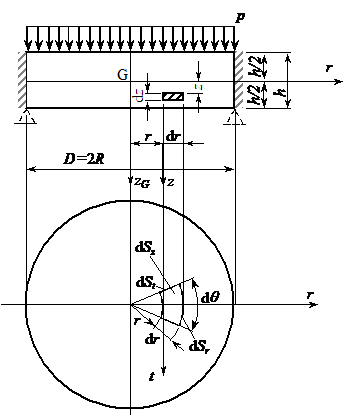
Fig. XVIII.1 Placa circulara simplu rezemata pe contur

Simetria placii, a reazemului si a starii de solicitare conduc la o deformare simetrica a placii. Studiul geometric arata ca suprafata mediana plana se modifica intr-o suprafata curba de revolutie cu axa prin deplasarea punctelor planului median, conform legii lui Kirchoff, numai dupa normala la planul median.

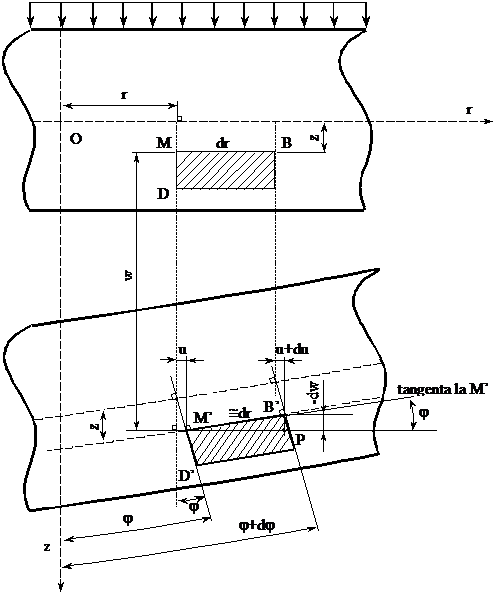
Fig. Studiul geometric al elementului de placa

Punctul M al volumului elementar se deplaseaza cu pana in punctul M', iar tangenta la suprafata deformata ce trece prin punctul mentionat formeaza unghiul notat cu cu orizontala, ceea ce exprima rotirea punctului M (rotirea punctului M D' in raport cu MD). Punctul B asociat punctului M prin pe directia se deplaseaza pe directia cu . Pe directia punctul M se deplaseaza cu , iar punctul B se deplaseaza cu .

Prin prisma simetriei se constata ca volumul elementar se poate lungi sau scurta pe directia r si t, fig. XVIII.1; pe directia avand loc o deplasare a placii in ansamblul ei, deformarile sunt insignifiante.

Din punct de vedere al lunecarilor simetria cazului studiat este compatibila doar cu lunecarile planelor S_r .

Prin prisma modului de calcul al deformatiilor se pot scrie urmatorele relatii:

• in triunghiul M'B'P avand in vedere semnul deplasarilor si rotirilor si tinand cont de faptul ca deplasarile liniare sunt infinitzetimale (, ):

; (XVIII.1)

• lungirea specifica radiala pe directia are in vedere lungirea calculata prin prisma deplasarii diferentiate a punctelor M si B ce definesc :

; (XVIII 2)

• lungirea specifica circumferentiala pe directia tangentei la cercul de raza in punctul M este evidentiata de noua circumferinta de raza a punctului M':

; (XVIII 3)

• deplasarea u a punctului M situat la distanta de planul median prin prisma rotirii a punctului este .

Prin prisma parametrului ce intervine in ecuatia diferentiala de echilibru a elementului de placa, lungimile specifice se calculeaza astfel:

, (XVIII 4)

iar este :

. (XVIII 5)

2 Aplicarea legii generalizate a lui Hooke

Asociat deformatiilor , , (nesemnificativ) si a lunecarilor posibile doar in planul  datorita simetriei rezulta o dispunere a tensiunilor conform figurii XVIII.3.

Fig. XVIII.3 Dispunerea tensiunilor

Deoarece si rezulta ca este o suprafata principala iar directia este indiferenta de marimea solicitarii si de dimensiunile placii circulare fiind o directie principala dupa care se dezvolta o tensiune normala principala.

Se observa:

• o variatie a tensiunii radiale pe directia ;
• tensiune circumferentiala constanta pe circumferinta;
• deoarece planurile paralele cu planul median se deformeaza fara sa se striveasca intre ele;
• o variatie a tensiunii tangentiale pe directia r din planul S_r.

Se constata ca elementul de placa se afla intr-o stare plana de tensiune, valorile tensiunilor calculandu-se prin prisma legii generalizate a lui Hooke (V.16) pentru o valoare z data, fiind dependente da variabilele si r.

, (XVIII.6)

. (XVIII.7)

3 Eforturi in placile circulare

Reprezentarea cumulativa a tensiunilor din sectiunile volumului elementar, se face sub forma cunoscuta a eforturilor.

In cazul placii, efortul nu mai pote fi dedus din exterior prin aplicarea torsorului de reducere. Efortul poate fi dedus functie de solicitarea exterioara pe intreaga circumferinta. Pentru a putea reprezenta efortul pe placa elementara de grosime h, ( din formulele precedente devine ), sarcina exterioara uniform distribuita fiind reprezentata de p, se considera intensitatea efortulurilor (efortul pe unitatea de lungime) T₁, M₁, obtinute din raportarea acestora la lungimea pe care se manifesta (fig. XVIII.4).

In cazul studiat conform solicitarii, eforturile moment sunt pozitive, suprafata de dedesubt este intinsa iar efortul forta taietoare pe portiunea considerata este negativ. Marimile si unitatile de masura ale intensitatii eforturilor sunt:

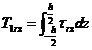[N/m] unde [N], (XVIII.8)

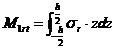[Nm/m] unde [Nm], (XVIII.9)

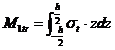[Nm/m] unde [Nm]. (XVIII.10)

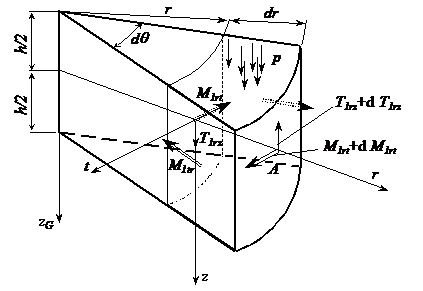
Fig. XVIII.4 Reprezentarea eforturilor

Prin prisma expresiilor lui si eforturilesi capata forma:

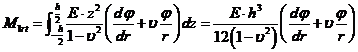, (XVIII.11)

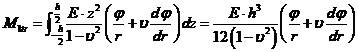, (XVIII.12)

in care:

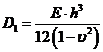, (XVIII.13)

unde este  modulul de rigiditate cilindrica a placii pe unitatea de lungime;

, (XVIII.14)

. (XVIII.15)

4 Studiul static

Din echilibrul fortelor dupa (pe axa t nu avem eforturi forta, iar dupa axa efrturile sunt egale si de sens contrar) rezulta:

, (XVIII.16)

. (XVIII.17)

Amplificand cu si neglijand diferentele de ordinul doi, rezulta:

, (XVIII.18)

sau:

, (XVIII.19)

, (XVIII.20)

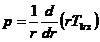, (XVIII.21)

Prin integrare rezulta:

. (XVIII.22)

Din calculul integralei rezulta:

(XVIII.23)

de unde:

. XVIII.24)

Prin relatia (XVIII.24) se face legatura dintre solicitarea exterioara p si efortul forta taietoare T.

De mentionat ca in cazul placilor circulare incarcate simetric, forta taietoare poate fi determinata usor considerand conditiile de echilibru pentru o portiune centrala de forma cilindrica de raza decupata din placa.

Din echilibrul sarcinii exterioare cu efortul forta taietoare pe unitatea de lungime de pe suprafata laterala a cilindrului de aceeasi valoare pe o circumferinta de raza r, rezulta:

, (XVIII.25)

de unde:

. (XVIII.26)

Din echilibrul momentelor in planul in raport cu punctul A rezulta un echilibru al momentelor (momentele din planul sunt constante pe intreaga circumferinta, iar in planul nu exista) sub forma:

, (XVIII.27)

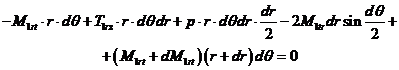(XVIII.28)

Amplificand cu si neglijand diferentiala de ordin superior rezulta ecuatia de echilibru a momentelor sub forma:

. (XVIII.29)

Relatia (XVIII.29) exprima legatura dintre eforturile M si T.

5 Functia a placii circulare incarcate simetric

Din analiza ecuatiilor de echilibru (XVIII.21) si (XVIII.29) se constata ca introducand in (XVIII.29) eforturile moment sub forma (XVIII.14 si (XVIII.15) si avand in vedere ca T_1rz poate fi dedus din (XVIII.21), rezulta o expresie de forma pentru o incarcare data p si o rigiditate D₁ a placii considerate.

Din (XVIII.29) rezulta:

XVIII.30)

XVIII.31

XVIII.32

de unde:

. (XVIII.33)

Integrand de doua ori expresia (XVIII.33 rezulta:

. (XVIII.34)

Constante de integrare si se determina din conditii la limita pentru fiecare caz concret. Astfel se fac referirile la rotiri, sageti, eforturi, care pot fi stabilite in mijlocul placii, pe conturul de rezemare, pe contururile libere, precum si pe frontiera intervalelor cu incarcari diferite avand in vedere continuitatea fibrei. De asemenea se au in vedere conditiile geometrice in situatiile de simetrie.

Inlocuind pe T_1rz (XVIII.24) prin integrari successive ale ecuatiei XVIII.34) rezulta:

(XVIII.35)

Prin cunoasterea functiei pot fi determinate momentele incovoietoare pe unitatea de lungime M_1tr si M_1rt , din expresiile (XVIII.11) si (XVIII.12) precum si sageata w din (XVIII.1). Cunoscand momentele incovoietoare se determina tensiunile din compararea expresiilor (XVIII.6), XVIII.7) si XVIII.11), XVIII.12), rezulta:

;

(XVIII.36)

;

Pentru rezulta tensiunile normale maxime din sectiunea de calcul considerata:

si (XVIII.37)

unde:

si

- moment de inertie axial al placii pentru latimea de o unitate;

- modul de rezistenta axial al placii pentru latimea de o unitate;

Se constata ca distributia tensiunilor orientate dupa cele doua directii r si t  variaza liniar pe grosimea placii fiind proportionale cu distanta de la punctul de calcul la suprafata mediana ca in cazul barelor (Navier). Planul neutru pentru si coincide cu suprafata mediana a placii, valorile extreme ale tensiunilor fiind pe suprafetele laterale.

Pentru determinare sagetii w se are in vedere (XVIII.1) in care se inlocuieste

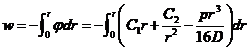XVIII.38)

XVIII.39)