Precizia mecanismelor cu parghii

PRECIZIA MECANISMELOR CU PARGHII

a)   Prin rezolvarea problemelor de sinteza cinematica se determina parametrii dimensionali ai mecanismului care realizeaza legea de miscare si conditiile suplimentare impuse. Acesta este mecanismul nominal, la care cuplele si elementele cinematice sunt construite geometric exact.

La mecanismul real, parametrii dimensionali se deosebesc fata de cei de la mecanismul nominal datorita erorilor de prelucrare si montaj, a uzurii in timpul functionarii etc. [23],[51],[62],[68].

Deoarece parametrii dimensionali reali difera fata de cei nominali, miscarea mecanismului real va fi diferita de cea a mecanismului nominal (miscarea dorita).

Erorile independente (elementare) sunt erorile datorate abaterilor constructiv-tehnologice ale elementelor si cuplelor cinematice. Acestea sunt formate din:

abateri dimensionale si pozitionale ale elementelor cinematice;

abateri dimensionale si de forma ale cuplelor cinematice.

Aceste abateri se incadreaza in limitele campurilor de toleranta STAS.

Erorile functionale (dependente) sunt erorile pozitiilor, definite ca diferente intre pozitia elementelor conduse ale mecanismului efectiv fata de pozitiile elementelor conduse ale mecanismului nominal la aceeasi pozitie a elementelor conducatoare.

Este necesar sa se stabileasca modul in care erorile independente influenteaza erorile functionale.

Se considera un mecanism cu grad de mobilitate , la care parametrul de pozitie independent este . Pozitiile elementelor sau ale punctelor mecanismului depind de pozitia elementului conducator si de parametrii dimensionali ai mecanismului:

,  (1.161)

in care: este un parametru de pozitie oarecare; , ,. - sunt parametrii dimensionali (constanti) ai mecanismului nominal.

Din cauza erorilor elementare , ,., valoarea parametrului de pozitie de la mecanismul real va fi diferita de cea de la mecanismul nominal cu eroarea de pozitie , deci:

              (1.162)

Dezvoltand in serie Taylor si retinand numai termenii de gradul intai se gasesc erorile pozitiilor:

                           (1.163)

Se observa ca eroarea totala este functie liniara de erorile elementare, pentru o pozitie data a elementului conducator.

Cunoscand in doua pozitii erorile pozitiilor si se poate determina eroarea deplasarilor in acest interval:

.           (1.164)

Prin derivari succesive, in raport cu timpul, se obtin erorile vitezelor si acceleratiilor.

b) Ca un exemplu se va determina eroarea de pozitie a punctului B de la un mecanism manivela - piston (fig. 1.53), tinand cont de abaterile lungimilor elementelor.

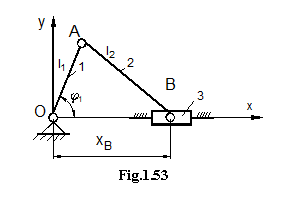Proiectand ecuatia conturului vectorial CAB pe axele de coordonate se poate exprima coordonata punctului B:

          (1.165)

Expresiile derivatelor partiale sunt:

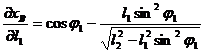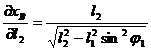,.           (1.166)

Erorile de pozitie partiale, produse de abaterile si ale lungimilor manivelei si bielei, vor fi:

; .                           (1.167)

Eroarea totala de pozitie , conform relatiei (1.164), va fi:

.          (1.168)