Momente de inertie pentru domenii materiale omogene uzuale

Momente de inertie pentru domenii materiale omogene uzuale

1)     Dreptunghi

Se considera un element infinit mic dA dintr-o sectiune dreptunghiulara cu laturile b si h ca in Figura 3.13.

Analizand sectiunea dreptunghiulara din Figura 3.13.a, putem exprima elementul de arie sub forma :

dA = b dz (3.64)

Momentul de inertie axial, calculat in raport cu axa Oy, este

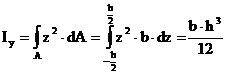(3.65)

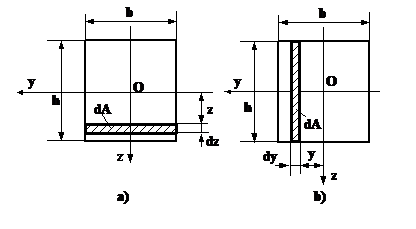
Fig. 3.13.

Raza de inertie este, corespunzator relatiei sale de definitie

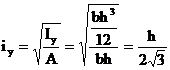(3.66)

Analizand sectiunea din Figura 3.13.b, putem exprima elementul de arie sub forma :

dA = h dy    (3.67)

Momentul de inertie axial, calculat in raport cu axa Oz, este 

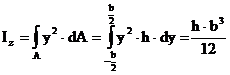(3.68)

Raza de inertie este, corespunzator relatiei sale de definitie

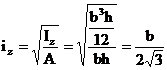(3.69)

2)     Cerc

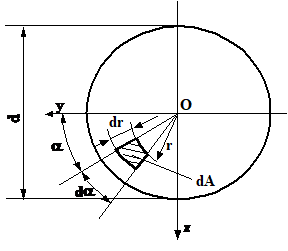
Se considera un element infinit mic dA dintr-o sectiune circulara de raza r ca in Figura 3.14.

Analizand sectiunea din Figura 3.14, putem ex-prima elementul de arie sub forma

(3.70)

Momentul de inertie polar,este

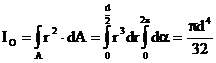  (3.71)

Fig. 3.14.

Din motive de simetrie, momentele de inertie axiale sunt egale

(3.72)

Momentul de inertie axial este, prin urmare

(3.73)

Raza de inertie este, corespunzator relatiei sale de definitie

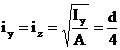  (3.74)

3)     Inel circular

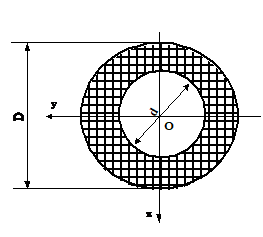
Momentul de inertie polar

(3.75)

Momentul de inertie axial

   (3.76)

Raza de inertie este, corespunzator relatiei sale de definitie

Fig. 3.15.

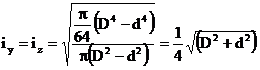(3.77)