Profitul si surplusul firmei

Daca la nivelul consumatorului, obiectivul final este maximizarea utilitatii, la nivelul firmei - fie ea de productie, de comercializare, de prestari servicii etc. - scopul final este acela de maximizare a profitului.

1.     Definirea functiei profitului

Fie o firma f in competitie pe piata unui aumit tip de bun.

Def. Functia profitului la nivelul functiei f, in functie de cantitatea de output obtinuta (sau comercializata, volumul de servicii prestatate etc.) q este data de :

p: R₊ R

unde p(q) = V(q) - C(q) fig. 1

iar V(q) - reprezinta venitul la nivelul firmei f (cifra de afceri);

C(q) - reprezinta costul la nivelul firmei f.

In functie de tipul de competitie pe piata si modul de calcul al costului, avem diferite forme pentru functia profitului, astfel:

daca pe piata unui produs, ce constituie obiectul de activitate al firmei f, exista competitie perfecta (ceea ce inseamna ca pretul p este dat), atunci:

p(q) = q^.y - C(q)fig. 2

Totodata, in acelasi tip de competitie putem face analiza profitului pornind de la faptul ca avem cantitatea de output q ca o functie de consumul de factori q=q(r.r_m) si de asemenea costul C = C(r), cu pretul ouputului si al inputurilor fixat:

p(p,x) = V(p,q) - C(x,q) = p^.q(r) - x^.r

= p^.q - C(x,q) =

fig. 3

- daca pe piata produsului respectiv exista competitie imperfecta, la nivelul firmei f avem:

p(q) = V(q) - C(q)

fig. 4

unde, de data aceasta, functia venitului are forma:

V(q) = p(q)^.q

cu p(q) reprezentand functia inversa a cererii, cu panta negativa.

Observatie: profitul se poate calcula - in cazul competitiei imperfecte - si altfel, si anume spre exemplu in cazul cartelului, unde profitul firmei f poate fi proportional cu cantitatea de output vanduta pe piata de firma in discutie, adica:

unde: p_f - reprezinta profitul firmei f;

q_f - cantitatea de output cu care vine pe piata firma f;

q - cantitatea totala de output pe piata, cu:

F - numarul total de firme din cadrul cartelului

p - profitul la nivelul cartelului

In cadrul unei firme ce obtine multioutput q=(q₁, q₂, ., q_n)^T, folosind m inputuri r=(r₁, ., r_m)^T, profitul firmei va fi:

p(q,r) = p^.q - xr, sau analitic:

fig. 5

2.     Proprietati ale functiei profitului

Vom lua, pentru inceput, in discutie functia profitului p(p, x), unde presupunem indeplinite proprietatile C₁-C₆ (C reprezinta functia cost) de catre functia cost c(x,q).

p₁) functia profitului p(p, x)> 0, aceasta inseamna ca firma se angajeaza ori in activitatea de a nu face nimic, si atunci V=C=0, fie desfasoara o activitate in urma careia V 0, C 0 dar totusi V=C, sau ultima situatie posibila V 0, C 0, dar V>C (altfel nu are sens a desfasura o asemenea activitate).

p₂) Functia profitului p(p, x) este crescatoare in p, ceea ce inseamna ca daca pretul outputului creste, atunci creste si profitul. Altfel scris, avem ca daca p¹>p², atunci p(p¹, x) > p(p², x).

Demonstratie. Presupunem ca pentru pretul p² nivelul outputului este q². Fie p¹ pretul corespunzator nivelului outputului q¹, cu p¹>p². Cantitatea q¹ poate fi mai mare sau egala cu q².

In prima situatie q¹=q², sporul de profit va fi:

p(p¹, x)-p(p², x) = (p¹-p²)q²>0

In a doua situatie q¹>q², sporul de profit va fi:

p(p¹, x)-p(p², x) = p¹q¹-C(x, q¹)-p²q²+C(x, q²)

=p¹(q²+a)-p²q²+C(x, 1)q²-C(x, 1)(q²+a)

=(p¹-p²)q²+[p¹-C(x, 1)]a>0

p₃) Functia profitului p(p, x) este descrescatoare in x, ceea ce inseamna ca daca vectorul preturilor factorilor x¹ este mai mare sau cel putin egal cu un alt vecor x², atunci profitul obtinut folosind factorii la preturile x¹ este mai mic sau cel mult egal cu profitul obtinut la preturile x².

Demonstratie. Din x¹>x² rezulta ca diferenta dintre cele doua niveluri ale profitului:

p(p, x¹)-p(p, x²) = pq¹-C(x¹, q¹)-pq²+C(x², q²)

=p(q¹-q²)+[C(x², q²)-C(x¹, q¹)]

= p(q¹-q²)+[C(x², q¹)-b-C(x¹, q¹)]

= p(q¹-q²)+[C(x², q¹)-b-C(x², q¹)-d]

cu b, d>0 astfel incat:

C(x², q¹)-b=C(x², q²) si C(x², q¹)+d=C(x¹, q¹)

Rezulta, deci, ca:

p(p, x¹)-p(p, x²)<0

p₄) Functia profitului p(p, x) este convexa si continua in (p, x).

Demonstratie. Functia p(p, x) este convexa daca oricare ar fi doua perechi de preturi (p¹, x¹) si (p², x²) ce maximizeaza profitul pentru cuplurile (r¹, q¹) si (r², q²), si de asemenea oricare ar fi perechea (p³, x³)=(ap¹+(1-a)p², ax¹(1-a)x²), cu aI(0, 1), atunci valoarea profitului p(p³, x³) se gaseste pe segmentul [p(p¹, x¹), p(p², x²)].

Avem din definitia functiei profitului, urmatoarele:

p(p¹, x¹) p¹q³-x¹r³;

p(p², x²) p²q³-x²r³

iar:

p(p³, x³)=a(p¹q³-x¹r³)+(1-a)(p²q³-x²r³)

Deci:

p(p³, x³)=ap(p¹, x¹)+(1-a p(p², x²)

p₅) Functia profitului p(p, x) este omogena de grad 1, adica daca preturile atat ale factorilor, cat si outputului se multiplica cu l, atunci si profitul se multiplica tot cu acea constanta l

Demonstratie: Avem:

p lp, lx)=(lp)q-C(lx, q)=lpq-lC(x, q)=lp(p, x)

p₆) Daca p(p, x) este o functie diferentiala in p si x, atunci exista un unic output

si o singura combinatie:

cu

Observatie: Hotelling a demonstrat, de asemenea, ca daca exista un set (q, r) ce maximizeaza profitul, atunci functia profitului este diferentiala.

Analiza statica comparata

Fie perechea (p, x) a preturilor outputului si respectiv factorilor, ce corespunde punctului (q, r) de maximizare a profitului si de asemenea, perechea (p¹,x¹) ce corespunde punctului (q¹, r¹) de maximizare a profitului. Cu aceste notatii avem ca:

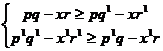
de unde se obtine, adunand cele doua relatii, ca:

pq-xr-pq¹+xr¹+p¹q¹-x¹r¹-p¹q+x¹r 0

fig.6

Observatie: Daca x¹=x atunci avem:

(p¹-p)(q¹-q) 0

ceea ce inseamna ca daca pretul oferit p¹ este mai mare sau egal cu p, atunci va creste cantitatea oferita, q¹ q.

Daca pana acum, in cadrul proprietatilor functiei profitului, am avut in vedere numai cazul functiei p(p, x) corespunzatoare pentru o firma in competitie perfecta, in continuare se va analiza situatia profitului firmei in conditiile in care costul este o functie numai de output.

Atunci cand functia de productie este monooutput, functia profitului:

p(q)=pq-C(q)

trebuie sa fie o functie concava (aceasta deoarece conditia de ordinul I este ^p _q=0, iar conditia de ordinul II care asigura ca punctul de extrem sa fie maxim este ²p q²=0).

Pentru o functie de productie si in consecinta si de profit, multioutput:

conditiile de maximizare a profitului sunt date:

-fie pornind de la matricea hessiana:

cu:

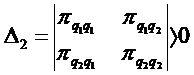
D₃<0, D₄>0, .

In general, D_I este negativ dupa cum I este impar, respectiv par, unde D_Ireprezinta minorii matricei hessiene;

fie cu ajutorul diferentialei totale, si anume diferentiala totala de gradul doi in punctul sectionar q*=(q^*₁, q^*₂, ., q^*_n) sa fie negativ definita, adica:

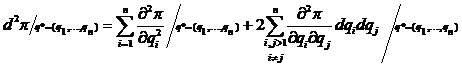
fig.7

Analiza in dinamica. Determinarea valorii prezente a firmei

Pornind de la valoarea profitului estimat a fi obtinut in viitor la o firma, se poate determina valoarea prezenta a firmei, indicatorul primordial in operatiunea de evaluare a acesteia.

Ca urmare, vom presupune analiza pe orizont infinit de timp si presupunem de asemenea cunoscute (valori estimate) valorile p₀ p₁ p_t, cu t

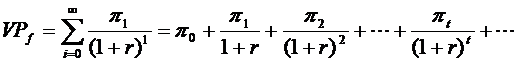
Atunci:

Fig.9

unde: VP_f - valoarea prezenta a firmei f

r - rata anuala de discount

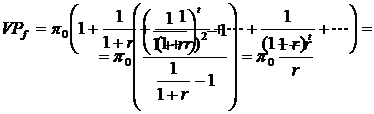
Observatie: In ipoteza ca p₁ p_t+1, unde t=0, 1, 2, . atunci valoarea prezenta a firmei va fi:

deoarece am avut o progresie geometrica cu ratia 1/(1+r).

Exemplul 1. Daca presupunem o firma f cu p₀ p₁=.=1 milion lei, iar r=40%, atunci valoarea prezenta a firmei este:

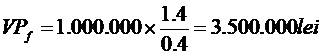
3.     Maximizarea profitului pe termen scurt

Fie o firma f cu doua inputuri , cu fixat undereprezinta cheltuielile fixe la nivelul firmei.

Pentru o piata in competitie perfecta, atat la output cat si la inputuri, avem de rezolvat la nivelul firmei f, urmatoarea problema de optim:

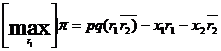
cu p,x - vectori de preturi dati, iar functia de productie este, de asemenea, cunoscuta. Rezolvarea problemei, presupune gasirea cantitatii optime de input r₁^* ce trebuie consumata, astfel incat firma f sa isi realizeze obiectivul sau de maximizare a profitului. Pentru aceasta trebuie sa fie indeplinite cele doua conditii:

-conditia de ordinul I:

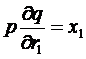
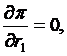
ceea ce implica

semnificand faptul ca productivitatea marginala in expresie valorica, sa fie egala cu pretul factorului;

-conditia de ordinul II:

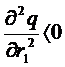
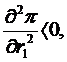
sau echivalent

ceea ce este adevarat, din ipotezele asupra functiei de productie.

Daca firma doreste obtinerea unui aumit nivel de profit, atunci:

de unde se obtine expresia lui r₁, functie de niveluldat al profitului

Exemplul 2. Presupunand functia de productie de tip Cobb-Douglas, cu factorul

dat,, avem ca relatia de mai sus se scrie:

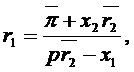de unde curba izoprofitului este:

cu

ceea ce reprezinta o paralela cu aza r_2:

Se observa ca pe masura ce nivelul creste, curbele izoprofitului se deplaseaza in sus.