Tehnici de decizie si clasificare a formelor

Scopul lucrarii

Lucrarea are ca scop prezentarea unor concepte de baza necesare in procesul de clasificare a formelor.

Notiuni teoretice

1.1. Selectarea trasaturilor

Este necesara determinarea unei clase optimale de trasaturi care sa permita separarea obiectelor ce trebuiesc recunoscute. Ansamblul optimal de trasaturi este functie de familia de obiecte de recunoscut. Adaugarea sau eliminarea unui obiect din aceasta familie poate modifica ansamblul trasaturilor optimale. Nu exista o teorie generala pentru selectarea parametrilor, dar se utilizeaza tehnici pentru aprecierea puterii discriminante a unei clase de trasaturi.

Printre tehnicile folosite pentru marirea relevantei informatiilor furnizate de vectorul de trasaturi mentionam:

Normarea trasaturilor - procedeu util atunci cand extragerea trasaturilor este facuta din mai multe surse diferite;

Ponderarea trasaturilor - permite accentuarea trasaturilor esentiale ale procesului de clasificare;

Transformarea sau combinarea trasaturilor - astfel incat utilizarea lor sa fie mai usoara;

Analiza componentelor principale (Karhunen- Loeve) - determina vectori ortogonali de dimensiuni mai reduse;

Reducerea dimensiunii vectorului trasaturilor - pe baza unor metode matematice utilizand transformate diagonale, rotationale, transformata Fourier, Walsh/Hadamard.

1.2. Clasificarea propriu-zisa

Exista doua moduri de abordare a clasificarii propriu-zise:

Clasificarea controlata - presupune existenta unui set de forme a caror apartenenta la clase este cunoscuta.

Clasificarea necontrolata - in care nu se face apel la o cunoastere prealabila a apartenentei unei forme la o clasa.

1.2.1. Vectori de forma si spatiul formelor

Fiecare caracteristica poate fi considerata ca fiind o variabila intr-un spatiu n-dimensional unde fiecare caracteristica este atribuita unei dimensiuni. Fiecare forma apare ca un punct in spatiul formelor. Cand o forma este descrisa de mai multe caracteristici ea poate fi privita ca un vector X, denumit vectorul de forma. Acest vector este dat de relatia:

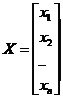                              (2.1)

unde x_i, i= 1,., n reprezinta cele n caracteristici.

Spatiul formelor notat cu W_X poate fi descris cu ajutorul relatiei

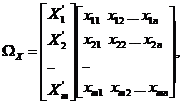                              (2.2)

unde X^'_i desemneaza vectorul transpus a lui X, iar m numarul de forme.

1.2.2. Tehnici de decizie si clasificare

Conceptul de clasificare al formelor poate fi inteles ca o partitionare a spatiului caracteristicilor acestuia. Clasificarea formelor, adica atribuirea fiecarui vector posibil sau punct din spatiul caracteristicilor clasei din care face parte, poate fi interpretata ca o partitionare a acestuia in regiuni (domenii) reciproc exclusive, fiecare domeniu apartinand unei clase de forme particulare. Din punct de vedere matematic acest gen de problema de clasificare poate fi definita sub forma unei functii discriminant. Astfel fie w₁ w₂ w_m cele m clase de forme posibile cu proprietatile:

w₁ w₂ .w_m W_X (2.3)

si

w₁ w_{2 .}w_m = F.

Unde cu F s-a notat multimea care constituie frontierele dintre clase, iar cu X s-a notat vectorul de forma. In acest caz functia discriminant D_j(X) asociata clasei de forme w_j, j =1,., m are proprietatea ca daca forma reprezentata prin vectorul X face parte din w_i, fapt pe care-l vom simboliza X w_i, cu i specificat, atunci valoarea lui D_i(X) trebuie sa fie cea mai mare, adica pentru toti X w_i va fi indeplinita conditia

D_i(X) > D_j(X); i,j = 1, ., m, i j. (2.4)

In felul acesta limitele de partitionare ale spatiului caracteristicilor (desemnate anterior cu F), denumite si limite de decizie, pot fi exprimate cu ajutorul relatiei

F = D_i(X) - D_j(X) = 0; i, j=1,.,m, i j                  (2.5)

Au fost propuse foarte multe forme pentru functii discriminant D_i(X), forme ce satisfac conditia (2.4). dintre acestea vom mentiona in continuare doar pe cele mai importante.

1.2.3. Functii discriminant liniare

Intr-un spatiu bidimensional aceste functii sunt liniare si pot fi scrise sub forma:

x₁-mx₂-b=0,                   

sau                    

W₁x₁+W₂x₂+W₃x₃=0                                (2.6)

unde:

m - este coeficientul unghiular,

b - termenul liber,

iar W₁= 1, W₂= -m si W₃= -b.

Intr-un spatiu n- dimensional functiile sunt hiperplane de forma:

W₁x₁+W₂x₂+..+W_nx_n+W_n+1= 0 (2.7)

In acest caz functia discriminant D_i(X) asociata clasei de forme w_i reprezinta o combinatie liniara a caracteristicilor x_i, i =1,.,m, data in relatia:

D_i(X)= W_i,kx_k+ W_i,n+1 , I =1,.,m    (2.8)

Ecuatiile hiperplanelor date de relatia (1.8), pentru m clase de forme, pot fi scrise matriceal astfel:

D(X)=

Unde:

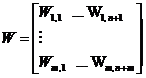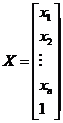si          (2.9)

In vectorul X s-a introdus suplimentar termenul 1 pentru a da posibilitatea efectuarii operatiei de inmultire.

Limita de decizie dintre regiunile W_x corespunzatoare claselor w_i si w_j este de forma:

D_i(X) - D_j(X) = W_kx_k+W_n+1; k = 1n; (2.10)

unde:

W_k=W_i,k - W_j,k

si

W_n+1=W_i,n+1-W_j,n+1.

Ecuatia (2.10) reprezinta ecuatia unui hiperplan din spatiul caracteristicilor W_x, numit si plan de decizie. Pentru a ilustra modul de utilizare a functiilor discriminant liniare prezentam un exemplu in care avem doua forme intr-un spatiu bi-dimensional. Fie formele X₁ si X₂ date de:

si

si functia de decizie D(X) = 0 data de relatia:

Relatia de mai sus poate fi scrisa sub forma:

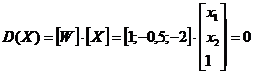
Daca inlocuim pe X₁ si X2 in D(X), obtinem:

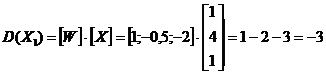
si respectiv

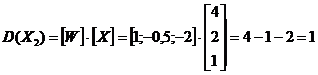
Pentru orice punct aflat deasupra lui D(X) = 0, D(X) este pozitiv si negativ pentru punctele de sub dreapta. Astfel, pentru cazul a doua clase, polaritatea in evaluarea lui D(X) determina la care clasa apartine forma data (Fig. 2.2-1).

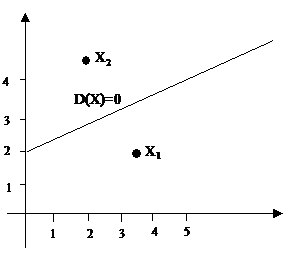
Fig. 2.2‑1Functia de decizie liniara in doua dimensiuni.

In cazul in care este necesara discriminarea pentru mai mult de doua forme sunt necesare doua sau mai multe functii de decizie. Pentru aceasta situatie exista trei tipuri de clasificatori.

i)        Tipul 1 utilizeaza o functie de decizie care imparte spatiul formelor in doua clase. Prima clasa notata cu w_i contine o singura forma, iar cea de a doua clasa contine restul formelor. Pentru a asigura apartenenta unei forme la clasa w_i este suficient sa fie indeplinita conditia D_i(X)>0 si D_j(X)<0 pentru toti i, j. Pentru n clase sunt necesare n functii de decizie.

ii)       Tipul 2 utilizeaza functii de decizie care separa spatiul formelor in doua regiuni. Prima regiune contine doua clase, iar cea de-a doua restul claselor. Separarea celor doua clase w_i si w_j se face cu ajutorul unei functii de decizie de forma D_ij(X) = 0. Apartenenta unei forme la clasa w_i sau w_j este asigurata daca D_ij(X) > 0.

iii)     Tipul 3 reprezinta un caz special al tipului 2 de clasificare. Din analiza figurilor 2.2-2a si 2.2-2b se observa prezenta unui spatiu nedeterminat care apare in interiorul triunghiului format din cele trei drepte corespunzatoare functiei de decizie. Punctele din interiorul acestui triunghi nu pot fi atribuite la nici una din cele trei clase. Pentru a elimina aceasta nedeterminare, functia de decizie de tipul 2, D_ij(X) = 0 este inlocuita cu D_i(X)-D_j(X) = 0, unde D_i(X) si D_j(X) sunt functii de decizie de tipul 1. Pentru ca o forma sa fie atribuita clasei w_i este necesar, in acest caz, indeplinirea conditiei D_i(X)>D_j(X) pentru toti j i (vezi fig. 2.2-2c).

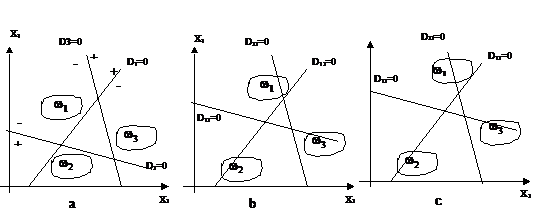
Fig. 2.2‑2 Functii de decizie multi-categorie: a-tipul 1; b-tipul 2; c-tipul 3.

Daca clasele pot fi separate utilizand tipul 1 de clasificare, regiunile in care este prezenta clasele vor fi mai compacte, fapt care conduce la o mai buna identificare a claselor decat in cazul utilizarii tipului 2 sau 3 de clasificare. In schimb, insa, regiunea de nedeterminare este mare. Daca in aplicatia practica apar forme in regiunea de nedeterminare rezultate in urma aplicarii tipului 1 de clasificare, poate fi incercata utilizarea tipului 2 de clasificare, in care regiunea de nedeterminare este mai mica sau a tipului 3 (tipul 3 de clasificare are dezavantajul ca timpul de calcul este mare)

1.2.4. Clasificatorul de distanta minima

O importanta clasa de clasificatori se bazeaza pe valoarea distantelor dintre forma de intrare si un set de vectori de referinta sau puncte prototip din spatiul caracteristicilor (prototipurile sunt forme a caror apartenenta la clase este cunoscuta). Daca vom presupune ca sunt cunoscuti m vectori de referinta, notati cu R₁, R₂,.R_m, cu R_j asociat clasei w_j atunci clasificatorul de distanta minima va atribui forma de intrare X clasei w_i daca distanta dintre aceasta si vectorii de referinta este minima,

adica X w_i daca d = X-R_i = minim.                (2.11)

Consideram doua grupe de puncte distincte in spatiul formelor si ne propunem sa determinam functia de decizie care va putea separa spatiul formelor in doua regiuni care vor corespunde celor doua clase. Initial vom determina vectorii de referinta pe care ii vom considera reprezentand centrele celor doua grupari de puncte. Valoarea punctelor prototip poate fi calculata cu o relatie de forma :

                   (2.12)

unde N reprezinta numarul de forme dintr-o grupare. Distanta dintre o forma X si centrul gruparii R (R este de forma R = (r₁, r₂,.,r_m)) este data de relatia d = X-R . Daca consideram ca cele doua grupari se afla intr-un spatiu bi-dimensional, atunci d va avea urmatoarea forma :

d² = (x₁ - r₁)² +(x₂ - r₂)² = x₁² - 2x₁r₁ + r₁² + x₂² - 2x₂r₂ + r₂².

In cazul cand avem mai mult de doua clase, distanta dintre o forma X si R_i al gruparii i este data de :

         (2.13)

Deoarece este aceeasi pentru toate clasele, el poate fi eliminat. Daca inmultim relatia (1.13) cu -0.5, vom obtine :

                                  (2.14)

Deoarece d_i² a fost inmultit cu un numar negativ rezulta ca cea mai mare functie de decizie (max D_i(X)) identifica distanta minima si deci clasa lui X.

Pentru determinarea termenilor W, din functia de decizie se utilizeaza relatia (2.14) si rezulta , pentru i = 1,.., n si .

Din cele spuse anterior rezulta ca un clasificator de distanta minima este un clasificator liniar. Performanta unui astfel de clasificator depinde evident de modul cum sunt alesi vectorii de referinta dar si  de felul cum sunt evaluate distantele. Cele mai frecvente distante utilizate sunt cele derivate de distanta generala Minkovski.

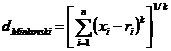                                  (2.15)

Astfel, pentru k = 2 se obtine binecunoscuta distanta Euclidiana.

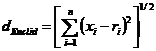    (2.16)

Pentru k = 1 se obtine distanta Manhattan.

          (2.17)

Daca toate caracteristicile x_i si r_i, i =1,.,n sunt codificate binar (au doar valorile 0 sau 1), atunci distanta Manhattan poarta numele de distanta Hamming. Distanta Hamming este echivalenta cu numarul de caracteristici care sunt diferite in X si R. Aplicarea lui SAU EXCLUSIV, simbolizat aici prin XOR, permite calcului foarte rapid al distantei Hamming conform relatiei:

(2.18)

Distanta Tanimoto reprezinta distanta Hamming normalizata.

                  (2.19)

Exemplu de determinare a functiilor de decizie.

Fie un spatiu bidimensional ce contine un numar de trei clase w₁ w_2, w₃ Cele trei clase contin urmatoarele forme:

,

,

.

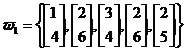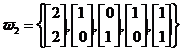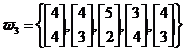Vectorii prototip ai claselor vor fi:

.

Functiile de decizie sunt de forma:

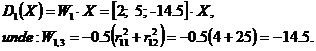
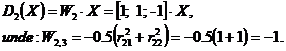
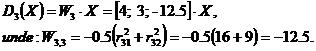
Pentru a testa acest clasificator se alege un punct din spatiul trasaturilor de forma:

si se substituie in , pentru I=1,2,3.

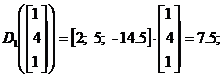
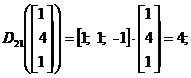
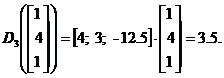
Se observa ca in acest caz avem D₁>D₂ si D₁>D₃ . Conform clasificatorului de tip 3, forma X este cea mai apropiata de de clasa 1 si cea mai indepartata de clasa 3. Rezulta ca X.

1.2.5. Alte tipuri de clasificatori

In literatura de specialitate sunt dezvoltati un numar mare de clasificatori, majoritatea avand ca punct de plecare clasificatorul distantei minime prezentat anterior. Dintre acestia cei mai importanti sunt:

i)        Clasificatorul vecinului cel mai apropiat. Acesta dezvolta un clasificator de distanta minima in raport cu mai multe seturi de vectori de referinta. Astfel, fie R₁, .,R_m cele m seturi de vectori prototip asociate, respectiv, claselor w₁ w_m si R_j^(k) setul de vectori de referinta din setul R_j, care apartin clasei w_j. In acest caz distanta dintre forma de intrare reprezentata prin vectorul X si setul de vectori de referinta R_j se defineste astfel:

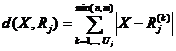, j = 1,.,m (2.19)

U_j fiind numarul de vectori de referinta din setul R_j. Clasificatorul ce utilizeaza acest tip de distanta va fi de forma

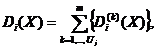i =1, ., m (2.20)

Acesti clasificatori sunt adesea denumiti clasificatori liniari pe portiuni sau clasificatori bazati pe cei mai apropiati U vecini.

ii)       Functii discriminant polinomiale.

Acestea dezvolta un clasificator de forma:

(2.21)

unde:  

k₁, k₂,..k_r = 1,.,n

pentru si

n₁, n₂,.,n_r = 0 si 1.

Limita de decizie dintre oricare 2 clase are forma unui polinom de ordinul r. In mod particular, pentru r = 2 obtinem o functie discriminant patrata cu

pentru k₁, k₂= 1,.,n; n₁, n₂ = 0 si 1 (2.22)

si L = (1/2) n (n+3).      

In aceasta situatie limita de decizie este un hiper-hiperboloid (in unele cazuri speciale aceste limite pot fi hipersfere sau hiperelipsoizi).

iii)     Clasificatorul Bayes

Se foloseste atunci cand distributia formelor nu este total disjuncta si exista suprapuneri semnificative ale valorilor trasaturilor diferitelor clase de forme.

In abordarea Bayesiana se folosesc cunostinte probabilistice despre trasaturile formelor si despre frecventa lor de aparitie.

Se presupune ca probabilitatea formelor clasei w_i este P(w_i Acesta inseamna ca apriori cunoastem probabilitatea de aparitie a unei forme din clasa w_I si, in absenta oricaror alte cunostinte, putem minimiza probabilitatea erorii de decizie presupunand ca forma necunoscuta apartine clasei cu probabilitatea P(w_i maxima. In luarea unei decizii de apartenenta se tine seama si de observatii asupra formelor.

Comportarea unei clase de forme este descrisa de probabilitatea conditionata p(x/w_i Probabilitatea p(x/w_i ne spune ca o trasatura masurata a unei forme apartinand clasei w₁ are valoarea x cu probabilitatea p(x/w_I Bazat pe aceste cunostinte se poate calcula probabilitatea a posteriori p(w_j /x) pentru o forma necunoscuta. Probabilitatea a posteriori p(w_j /x) a unei forme necunoscute ne spune ca daca o masuratoare facuta asupra formei necunoscute are valoarea x forma apartine clasei w_j cu probabilitatea p(w_j /x)

In multe aplicatii practice componentele lui x sunt valori ale variabilelor binare sau ternare asa incat x poate sa primeasca doar  una dintre valorile discrete ale lui m, v₁, .,v_m. In asemenea cazuri densitatea de probabilitatea a functiei p(x/w_j devine singulara; integrale ca si

sunt transformate in sume de forma

unde P(v_k|v_j este probabilitatea conditionata ca x = v_k, dindu-se astfel stara lui v_j

Calculul probabilitati conditionate p(w_j /x) se face pe baza formulei lui Bayes:

, (2.23)

unde:

si

m reprezinta numarul de clase.

Forma necunoscuta trebuie asignata clasei cu p(w_j /x) maxim. Formula poate fi generalizata pentru cazul unor vectori de trasaturi n dimensionali.

, (2.24)

unde:

,

m reprezinta numarul de clase si

X este vectorul de forma n-dimensional.

Functia discriminant dezvoltata pentru clasificatorul Bayes este de forma:

D_i(X) = P(w_i)*p(X/w_i),i =1,.,n (2.25)

1.3. PROBLEME PROPUSE

1.     Considerand un spatiu bidimensional si folosind functia discriminant liniara x₁-mx₂-b=0 pentru m =4/3 si b =2, scrieti un program care sa stabileasca apartenenta la unul din semiplanele delimitate de frontiera de decizie pentru perechi de forme, specificate de utilizator.

2.     Aceleasi cerinte ca la problema precedenta considerand urmatoarea functie polinomiala de decizie

x₁+x₂-x₃+1=0

intr-un spatiu tridimensional.

3.     Folosind metoda clasificatorului de distanta minimala si utilizind la alegere una din metodele de calcul a distantei minimale (Minkovski, Euclidiana, Manhattan), pe baza determinarii functiei de decizie in spatiul bidimensional, stabiliti apartenenta unei forme x din spatiul bidimensional uneia din cele trei clase de forme w₁ w₂ w₃ definite de utilizator.

Ind. Puteti folosi ca model clasele definite in exemplul dat pentru calculul functiei de decizie in cazul clasificatorului de distanta minimala.

4.     Fiind dat un spatiu bidimensional si trei clase de forme definite de utilizator, scrieti un program care sa stabileasca apartenenta unei forme necunoscute x la una din clasele date cunscand apriori probabilitatea de aparitie a unei forme din clasa w_i,i =1,.,3 P(w_i si probabilitatea ca o trasatura masurata a formei apartinand clasei w_i sa aiba o anumita valoare (p(x/w_i

Obs. P se exprima ca nr.cazuri favorabile /nr. cazuri posibile .

5.     Sa consideram problema densitatii conditionate pentru doua categorii unidimensionale data de distributia Cauchy

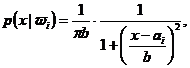i =1, 2.

Daca P(w₁)= P(w₂ aratati ca p(w₁/x)= p(w₂/x) daca x=

Calculati p(w₁/x) pentru cazul .Cum se comporta p(w₁/x) cand ?