sisteme bazate pe cunostinte - utilizarea retelelor bayesiene in fiabilitatea software

DEPARTAMENTUL PENTRU PREGATIREA PERSONALULUI DIDACTIC

SISTEME BAZATE PE CUNOSTINTE

UTILIZAREA RETELELOR BAYESIENE IN FIABILITATEA SOFTWARE

Capitolul I

INTRODUCERE

Sistemele bazate pe cunostinte, referite in continuare ca SBC, reprezinta nucleul pragmatic al domeniului calculatoarelor numit inteligenta artificiala. Aceste sisteme sunt aplicatii destinate rezolvarii problemelor ce necesita rationament bazat pe cunostinte.

Un sistem bazat pe cunostinte (SBC) este un program sau un pachet de programe care incorporeaza cunostinte dintr-un anumit domeniu si rezolva probleme dintr-o clasa bine definita de probleme aplicand strategii de rationare. Problemele care sunt rezolvate pot fi probleme de diagnoza, monitorizare, predictie, planificare, analiza, comanda si control etc. Solutia unor astfel de probleme implica efectuarea anumitor tipuri de rationamente numite artificiale, asemanatoare rationamentelor naturale, efectuate de om.

Componentele unui sistem bazat pe cunostinte:

- Baza de cunostinte (BC) - sistem cognitiv; cuprinde totalitatea cunostintelor (concepte, idei, teorii, reguli, metode, abstractizari, limbaje) din domeniul de aplicatie al SBC-ului.

- Motorul de inferenta (MI) - sistem rezolutiv; preia cunostintele din baza de cunostinte si le inlantuie printr-un mecanism de inferenta realizand rationamente care au rolul de a rezolva probleme din domeniul de aplicatie al SBC-ului.

- Modul de achizitie a cunostintelor (MAC); preia cunostintele specializate din domeniul de aplicatie al SBC-ului furnizate de expertii umani in domeniu sau de catre inginerul de cunostinte, din literatura de specialitate.

- Interfata cu utilizatorul (IU); are rolul de a asigura dialogul intre utilizator si sistemul de consultare a SBC-ului.

- Modul explicativ (ME); are rolul de a oferi explicatii ale rationamentelor efectuate de catre motorul de inferenta.

- Modul de invatare (MI); are rolul de a imbunatati performantele SBC-ului prin deducerea de noi cunostinte din cele existente, prin identificarea cunostintelor euristice performante, prin achizitia de noi cunostinte.

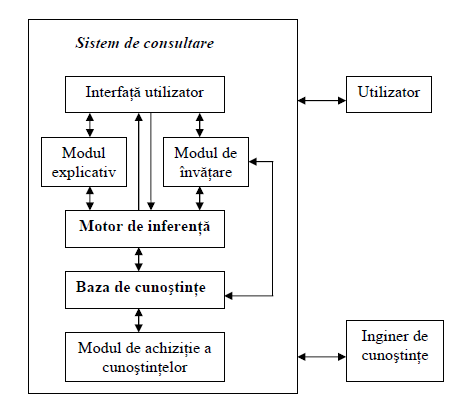
Arhitectura unui sistem bazat pe cunostinte

Implementarea sistemelor bazate pe cunostinte se poate realiza cu ajutorul:

- Limbajelor de programare clasice (C, Pascal);

- Limbajelor de programare specifice inteligentei artificiale (Lisp, Prolog);

- Generatoarelor de sisteme expert, asa numitele shell-uri de sisteme expert (H-Expert, VP-Expert);

- Instrumentelor specifice de dezvoltare a SBC-urilor (OPS5, KEE, Smash, SamIam); in cadrul laboratorului se va utiliza programul SamIam

In functie de tipul de aplicatie exista sisteme bazate pe cunostinte pentru:

- Interpretare

- Diagnoza si reparatie

- Consultare

- Monitorizare si control

- Predictie

- Planificare

- Proiectare

- Instruire

Capitolul II

RETELE BAYESIENE

Teoria de baza a retelelor bayesiene combina probabilitatea bayesiana si notiunea de independenta conditionala pentru a reprezenta dependentele dintre variabile (Pearl, 1986; Speigelhalter & Cowell, 1992). Pana in prezent retelele bayesiene s-au dovedit utile in multe tipuri de aplicatii ca sisteme expert medicale, de diagnostic al esecurilor, corespondenta tiparelor, recunoasterea vocala si, mai relevant pentru comunitatea riscurilor operationale, evaluarea riscurilor sistemelor complexe in medii cu miza ridicata.

Retelele bayesiene(Bayesian Belief Networks - BBN) fac posibila analiza in conditii de incertitudine si combina avantajele unei reprezentari vizuale intuitive cu o baza matematica solida in probabilitatea bayesiana. Cu BBN putem utiliza cunostintele expertilor in legatura cu dependentele dintre diferite variabile si sa proiectam in mod consistent impactul dovezilor asupra probabilitatilor rezultatelor incerte. BBN permit o insuflare de rigurozitate stiintifica cand distributiile de probabilitate asociate nodurilor individuale sunt doar "opiniile expertilor". Acest lucru poate sa creasca increderea in parerile expertilor, subliniind in acelasi timp imprecizia inerenta in asemenea tipuri de judecati.

O retea bayesiana este un graf orientat ale carui noduri reprezinta variabilele(discrete) incerte de interes si ale carui muchii sunt legaturile cauzale sau de influenta dintre variabile. Fiecarui nod i se asociaza un tabel de probabilitati. Acesta este un set de probabilitati conditionate ce modeleaza relatia de incertitudine dintre nod si parintele sau.

Cheia unui design de succes al retelelor bayesiene este descompunerea corecta a domeniului problemei intr-un set de propozitii cauzale sau conditionale despre domeniu. In loc sa cerem unui expert intreaga distributie unificata de probabilitati, care este evident o sarcina foarte dificila, putem aborda o strategie de tipul "divide-et-impera" si sa cerem detalii partiale ale modelului care au semnificatie in domeniul expertului. Obtinand aceasta descompunere, am specificat, ca rezultat natural al abordarii, si covarianta prin structura probabilitatilor conditionate.

In continuare avem nevoie ca expertul sa alcatuiasca tabelul probabilitatilor nodului(TPN) pentru fiecare variabila(nod): acest lucru poate fi facut fie utilizand date cronologice (prin invatarea parametrica bayesiana standard sau simularile Monte Carlo), fie cerand expertului sa furnizeze o serie de estimari subiective. Ideal ar fi ca aceste estimari sa se bazeze pe experienta si cunostinte, nu pe presupunere oarba.

Putem introduce cu usurinta distributii statistice discrete si continue in cadrul modelului retelei bayesiene, ca tabele de probabilitati ale nodurilor, si genera valori pentru aceste TPN-uri prin simulari Monte Carlo. Pentru functii continue trebuie sa aducem modelul la valori discrete corespunzatoare si in software-ul AgenaRisk aceasta operatie este realizata folosind o versiune avansata a algoritmului de discretizare dinamica prezentat in Kozlov si Koller (1997), permitand aproximarea solutiei atat pentru problemele statistice bayesiene clasice, implicand variabile continue, cat si pentru problemele hibride ce implica atat variabile discrete cat si continue.

Odata construita reteaua bayesiana, aceasta poate fi executata folosind un algoritm de propagare adecvat cum ar fi algoritmul arborelui de jonctiune. Acest lucru presupune calcularea tabelei unificate a probabilitatilor din structura probabilitatilor conditonate ale BBN intr-o maniera eficienta. Pentru aceasta se deriveaza automat din BBN reprezentarea unui graf teoretic, intermediar, numit arbore de jonctiune care permite executarea calculelor locale, modulare folosind un algoritm de transmitere a mesajelor. In esenta aceasta este o forma elaborata a teoremei lui Bayes. Intregul proces este complet automat, iar intr-un instrument ca AgenaRisk este ascuns expertului in domeniu.

Odata ce reteaua bayesiana a fost compilata, aceasta poate fi executata dinamic si prezinta urmatoarele doua caracteristici:

1. Efectele observatiilor introduse in unul sau mai multe noduri pot fi propagate in intreaga BN, in orice directie, si distributiile marginale ale tuturor nodurilor sunt actualizate.

2. Doar inferentele relevante pot fi facute in BN. Reteaua bayesiana foloseste structura dependentelor conditionale si cunostintele curente pentru a determina acele inferente care sunt valide.

Este important de observat ca volumul si complexitatea calculului implicate in folosirea retelelor bayesiene pot fi controlate din punct de vedere a memoriei interne si spatiului de stocare daca se foloseste o implementare eficienta a algoritmului arborelui de jonctiune. Totusi, multe pachete academice, open-source nu ofera implementari care sunt suficient de eficiente pentru a suporta modele mari de retele bayesiene, mai ales combinate cu simularea Monte Carlo. Dar implementari eficiente sunt posibile pentru clasa de retele bayesiene necesare modelarii problemelor de risc operational si pot fi asamblate relativ usor in unelte ca AgenaRisk.

STUDIU DE CAZ

UTILIZAREA RETELELOR BAYESIENE

IN FIABILITATEA SOFTWARE

Retelele bayesiene sunt cunoscute si sub numele de retele probabilistice cauzale, retele de probabilitate grafica, modele probabilistice cauza - efect si diagrame de influenta probabilistica, fiind de actualitate datorita folosirii lor ca o posibila solutie pentru situatiile in care informatia avuta la dispozitie este incompleta.

Deoarece pentru estimarea si predictia fiabilitatii software este nevoie de modele de fiabilitate care sa poata manevra: procese si produse diverse; relatii cauza si efect adevarate; incertitudine; informatie incompleta, utilizarea retelelor este adecvata in special pentru faptul ca exista instrumentul software SAMIAM care implementeaza calculul probabilistic, sofisticat al probabilitatilor conditionate fiind sprijinit si de o interfata grafica de top. Un BN (Bayesian Networks) este un graf care reprezinta relatii probabilistice intre variabile.

Cu BN este posibil sa se experimenteze dependente intre variabile diferite si sa se propage impactul unui lucru evident in probabilitati ale unor rezultate nesigure, cum ar fi fiabilitatea viitoare a unui sistem. Tot cu BN se mai pot reprezenta si manipula modele complexe ale fiabilitatii software, care pot sa nu fie implementate niciodata cu metodele conventionale. Alt avantaj este acela ca poate prezice evenimente bazat pe date partiale sau nesigure.

Se propune un exemplu despre cum se poate utiliza BN pentru a prezice fiabiliatea unui produs baza pe cunoasterea procesului si a produsului insusi (fig. 1).

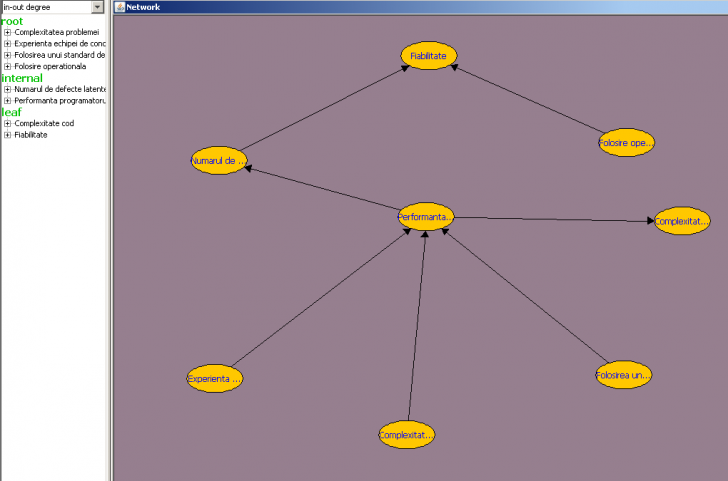
Figura 1 Utilizarea BN pentru predictia fiabilitatii folosind claritatea procesului si a produsului

Tabelul urmator cuprinde nodurile retelei baysene si starea lor.

Nodurile pot fi variabile discrete sau continue. De exemplu, nodul utilizand un standard de codificare este discret, avand doua valori: "da" si "nu", in timp ce nodul fiabilitate poate fi continuu (cum este probabilitatea de defectare).

Arcele sunt relatii cauzale (de influenta) intre variabile. De pilda, fiabilitatea software se defineste prin numarul de defecte latente si prin utilizarea operationala (frecventa cu care defectarile se pot declansa).

Aceasta relatie se modeleaza prin trasarea arcelor din nodurile "Numarul de defecte latente" si "Folosirea operationala" inspre "Fiabilitate".

Daca am sti ca exista un numar mare de defecte si un nivel ridicat de folosire operationala, atunci probabilitatea ca fiabilitatea sa fie mai mare ar fi mai mica decat atunci cand am sti ca sunt defecte putine si o utilizare scazuta.

In BN acest lucru se modeleaza cu tabela de probabilitate a unui nod, NPT (Node Probability Table).

Nodul de fiabilitate poate fi o variabila discreta, luand trei valori: joasa, medie si inalta.

NPT capteaza probabilitatile conditionate ale nodurilor parinte. Pentru nodurile fara parinti tabela probabilitatii nodului e o simpla probabilitate marginala.

Probabilitatile pentru NPT pot fi de tipul (tabelul 1):

probabilitati subiective (stabilite de experti);

probabilitati bazate pe date obiective (colectate pe proiecte similare).

Tabelul 1. Tabela NPT pentru nodul "fiabilitate"

Aceasta ipoteza se transpune in egalitatea probabilitatilor matematice pentru toate aceste noduri. Exista o tendinta de ignoranta care va duce la a se crede ca performanta programatorului e mult mai probabil scazuta decat inalta si de aceea numarul de defecte latente e mult mai probabil sa fie mai mare decat mic, ceea ce are ca urmare o fiabilitate scazuta, chiar daca nu stim nimic despre folosirea operationala a produselor (figura 2).

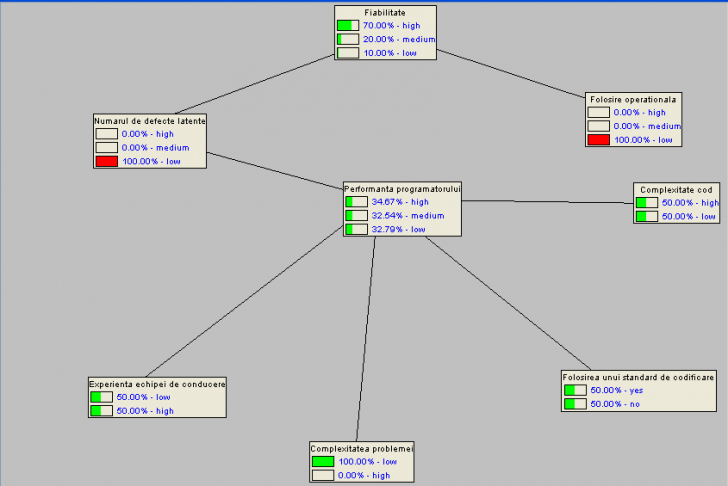
In continuare (figura 3), se face supozitia ca procesul e foarte bine controlat. Aceasta se materializeaza prin atribuirea valorii 1 probabilitatilor respective. Acest lucru va conduce la modificari semnificative asupra performantei codificatorului.

Impactul total asupra fiabilitatii nu e extraordinar (se schimba destul de modest fiabilitatea inalta).

Starea initiala a retelei bayesiene

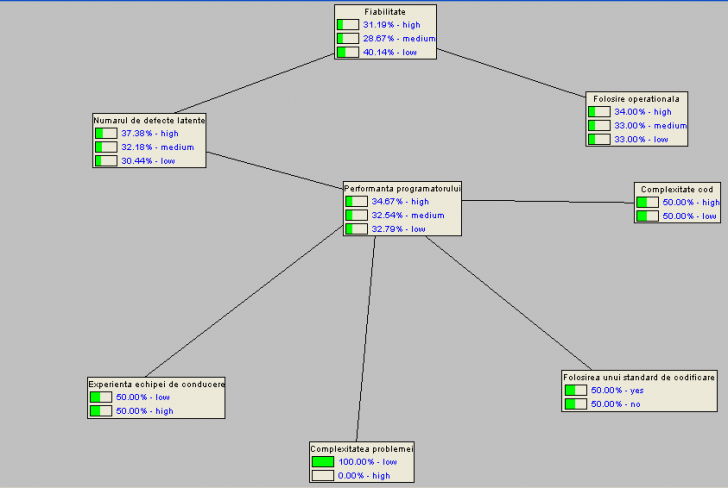
Pentru a verifica daca reteaua Baysieana a fost corect construita, s-au creat urmatoarea situatie ipotetica: numarul de defecte latente si folosirea operationala se incadreaza in procent scazut de 100%.

In acest caz scade fiabilitatea este mult mai intensa decat in starea initiala ajungand la 70%, diminuand pana la 10% coeficientul "low".

CONCLUZII

Consideram ca rezultatele studiului sunt bune, demonstrandu-se utilitatea retelelor baysene in studii si cercetari psiho-sociologice.

In acest studiu, s-a demonstrat versatilitatea Retelei Bayesiene cu privire la propunerile de programe dezvoltarea fiabilitatii echipamentelor si componentelor software.

S-a propus o retea Bayesiana de cercetare care intentioneaza sa ajute programatorii in aplicarea de programe pentru o fiabilitate cat mai buna a echipamentelor software.

Cercetarea s-a realizat in Scoala pentru Deficienti de Vedere Bucuresti.

BIBLIOGRAFIE

1.     Camelia GAVRILA, Sisteme bazate pe cunostinte - Universitatea Tehnica de Constructii Bucuresti;

2.     Camelia GAVRILA, Retele Bayesiene pentru prognoza si gestionarea cancerului de prostata - Universitatea Tehnica de Constructii Bucuresti;

3.     Revista Informatica Economica, nr 3 / 2000;