GEODEZIE

 

Prelucrarea observatiilor in retelele de nivelment si gravimetrie

Tema

Se dau:

1.      O retea de nivelment geometric de ordin superior (formata din reperii de nivelment A, B,

C, D) data prin coordonatele geodezice aproximative B, L;

-Cota provizorie si gravitatea absoluta pentru punctul A;

-Diferentele de nivel si gravitate rezultate in urma masuratorilor de nivelment geometric si respectiv gravimetrice, execute intre reperii de ordin inferior situati pe liniile de nivelment AB, AC, AD, BC, CD.

2.      O retea de nivelment trigonometric, dezvoltata din punctul A si formata din punctele A, A1, A2, A3, data prin coordonatele geodezice aproximative B, L.

-Distantele zenitale masurate si lungimile laturilor ;

-Inaltimea instrumentului si al semnalului in punct.

Se cer:

1.)O schita a celor doua retele ( inclusiv reperii de ordin inferior ).

2.)Compensarea retelei libere de nivelment geometric:

➢      Cu diferente de nivel masurate;

➢      In sistemul de altitudini ortometrice - sferoidice;

➢      In sistemul de altitudini normale.

3.)Compensarea retelei de nivelment trigonometric (luand ca fixa cota punctului A din compensarea retelei de nivelment in una din variantele b sau c :

➢     Necunoscuta unica pentru coeficientul de refractie pentru toata reteaua daca s-au facut toate compensarile de la punctul 2.

➢    Necunoscuta pentru coeficientul de refractie in fiecare punct de statie daca s-au efectuat compensarile de la punctele 2a si 2b sau 2a si 2c.

Memoriu Tehnic

I. Prelucrarea masuratorilor efectuate in retele de nivelment geometric geodezic

1.) Date initiale si scop:

Reteaua de nivelment este constituita din totalitatea punctelor luate in considerare la o anumita lucrare,dar si masuratorile care leaga aceste puncte intre ele; Reteaua de nivelmet in cazul nostru este o retea libera iar pentru asta trebuie sa se determine:

- diferentele de nivel masurate (Δh_ij^*)prin metoda nivelmentului geometric si reduse la unul din sistemele de altitudini cunoscut.

Pentru o prelucrare prin metoda masuratorilor indirecte este necesar ca numarul acestor masuratori sa fie mai mare decat numarul necunoscutelor implicate in model.

- lungimile traseelor urmate pentru determinarea diferentelor de nivel.

- altitudinea H_i a unuia sau a mai multor repere de nivelment din reteaua considerate.

- transformarea coordonatelor geodezice B, L in coordonate rectactangulare X, Y in proiectia Stereografica 1970 (ΔB - 1' ≈ 30 m, ΔL - 1'≈ 20 m)

- se determina cu ajutorul lui B si L coordonatele ΔX si ΔY(in m) si apoi se poatea afla distanta pe fiecare tronson cu relatia D_ij=

- alte informatii preliminarii utile la construirea modelului functional-stohastic,in mod deosebit cele care pot fi folosite pentru stabilirea unei matrice a ponderilor cat mai buna.

- altitudinile provizorii H_i^o pentru toate reperele noi din reteaua considerate, care se determina cu ajutorul diferentelor de nivel masurate , plecand de la altitudinea cunoscuta a unuia sau mai multor repere din retea.

Scop:

- determinarea altitudinilor pentru toate reperele noi ale retelei in sistemul de altitudini ales (valorile cele mai probabile) si preciziile cu care determinam aceste valori

- valorile cele mai probabile ale diferentelor de nivel si precizia cu care se cunosc aceste valori.

2.) Modelul de prelucrare:

Metoda folosita este cea a masuratorilor indirecte deoarece este usor de programat si totodata elementele necesare calcularii preciziei sunt si ele usor de calculat.

Intr-o retea de nivelment geometric geodezic trebuie sa determinam unele elemente preliminarii, cum ar fi altitudinea si gravitatea in fiecare reper.

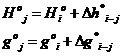
Unde:

H^o_j, g_j^{o -} altitudinea, respectiv gravitatea reperului pentru care se fac calculele.

H^o_i, g_i^{o -} altitudinea, respectiv gravitatea reperului din care se face transmiterea altitudinii.

ΔH^*_i,j, Δg_i,j^* - diferenta de nivel, respectiv diferenta de gravitate intre reperele i si j.

Diferentele de nivel trebuie reduse la sistemul de altitudini utilizat obtinand in final,valorile cele mai probabile ale altitudinilor punctelor in sistemul respective.

a.)      Reducerea diferentelor de nivel la un sistem de altitudini:

➢   Reducerea diferentelor de nivel la sistemul de altitudini ortometric-sferoidic:

^ORS reprezinta corectia de reducere a diferentei de nivel masurate la sistemul dealtitudini

ortometric-sferoidic, se calculeaza cu relatia:

f^*=0.0053(turtirea gravimetrica)

➢   Reducerea diferentelor de nivel la sistemul de altitudini normale:

^N reprezinta corectia de reducere a diferentei de nivel masurate la sistemul de altitudini normale, iar calculele se desfasoara astfel:

se determina valorile gravitatilor normale in punctele de la capetele tronsonului :

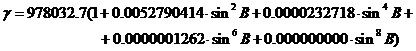
- se determina pentru aceleasi puncte gravitatea normala la altitudinea H a reperului de nivelment

- se determina corectia ortometrica sferoidica, datorata neparalelismului dintre suprafetele de nivel sicorectia datorata anomaliei gravitatii;

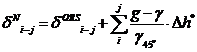
b.) Stabilirea modelului functional-stochastic:

➢    Modelul Gauss-Markov

v=Ax+l - modelul functional

unde :v - vectorul corectiilor

l- vectorul termenilor liberi

A - matricea coeficientilor

x - vectorul parametrilor

C_m=_o²Q_m - modelul stochastic

unde: C_m - matricea de varianta-covarianta

Q_m - matricea cofactorilor masuratorilor

_o² - varianta unitatii de pondere                     

Forma generala a ecuatiei de corectie pentru o diferenta de nivel masurata geometric :

b.1) ambele repere de la capetele tronsonului de nivelment sunt noi:

b.2) ambele repere de la capetele tronsonului sunt vechi:

Nu se executa masuratori directe de diferente de nivel daca nu exista cel putin un reper intermediar nou.

Unul din cele doua repere de la capetele tronsonului de nivelment este fix:

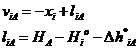
pentru reteaua de nivelment geometric termenul liber s-a determinat astfel

c.) Stabilirea ponderilor:

➢    ponderea e o valoare minima atasata unei masuratori prin care se exprima increderea in masuratoarea respectiva

➢    in geodezie consideram ca masuratorile sunt independente rezultand matricea cofactorilor o matrice diagonala

➢    la prelucrarea observatiilor efectuate in retelele de nivelment geometric se

utilizeaza in mod curent doua relatii pentru stabilirea ponderilor masuratorilor

Se calculeaza ponderea functie de lungimea traseului pe care s-au efectuat masuratorile:

L-lungimea traseului parcurs in [km]

( constanta din relatia de mai sus este aceeasi pentru toate diferentele de nivel care intervin in reteaua ce urmeaza a fi prelucrata,se alege astfel incat valorile ponderilor sa fie apropiate de unitate)

- prelucrarea se face prin introducerea unei ecuatii de pondere foarte mare. Ecuatia fictiva va avea toti coeficientii egali cu '1'pentru tote necunoscutelept a inlatura defectul de rang

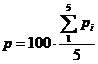
- o alta posibilitate este aceea de a utiliza numarul de statii in loc de lungumea traseului

d.) Normalizarea si rezolvarea sistemului normal:

- forma liniara

X=-N^-1 .A^{t .}P ^.L

unde: A - matricea coeficientilor sistemului liniarde ecuatii

P - reprezinta matricea ponderilor

N - matricea sistemului normal

x - matricea necunoscutelor sau solutziile sistemului de ec.

L - matricea termenilor liberi

I matricea unitate

e.) Calculul elementelor compensate:

(calculul valorilor cele mai probabile ale altitudinilor)

(calculul valorilor celor mai probabile ale diferentelor de nivel)

- verificarea compensarii trebuie sa satisfaca relatia:

f.) Calculul elementelor de precizie:

1.)    Abaterea standard a unitatzii de podere:

; m=5, n=4

unde :m - reprezinta numarul de masuratori

n - reprezinta numarul de necunoscute

d - defect de rang - in cazul nivelmentului d =1

2.) Abaterea standard de determinare a unei masuratori compensate

 ;

p_i reprezinta ponderea diferentei de nivel pe tronsonul considerat

3.) Abaterea standard de determinare a necunoscutelor:

; qsunt elementele de pe diagonala principala a matricii cofactorilor

necunoscutelor

4 Abaterea medie standard pe retea:

II. Prelucrarea masuratorilor efectuate in retele de nivelment trigonometric geodezic

1.) Date initiale si scop

➢    aceste masuratori se fac cu scopul de a determia punctele in retelele planimetrice

➢    trebuie sa stabilim o suprafata de referinta astfel incat sa poata fi fixata fata de suprafata aleasa ca referinta(la noi in Romania sistemul de altituni normale ca suprafata de refrinta cvasigeoidul si punct zero fundamental "Marea Neagra 1975")

➢   

Masuratori efectuate:

- directii orizontale zenitale sau distante zenitale

I si S - inaltimea instrumentului si inaltimea semnalului

D - distantele intre puncte care trebuie reduse la suprafata aleasa ca referinte

➢    H_ialtitudinea pentru cel putin un punct din reteaua din sistemulde altitudini considerat

trebuie sa o cunoastem

➢    Pentru coeficientul de refractie se alege o valoare:

Scop: - determinarea valorilor cele mai probabile si preciziile cu care au fost determinate

- valorile cele mai probabile ale masuratorilor si preciziile cu care au fost masurate

2.) Modelul de prelucrare:

Atunci cand se cunosc unghiurile verticale sau unghiurile zenitale si distanta inclinata sau orizontala intre cele 2 puncte considerate, atunci pot fi utilizate relatiile fundamentale ale trigonometriei petru determinarea diferentei de nivel intre cele 2 puncte

- conform principiului nivelmentului trigonometric trebuie sa cunoastem distanta dintre cele 2 puncte s_ij redusa la suprafata de referinta

- masuratorile corecte se obtin :

In nivelment trigonometric trebuie sa tinem cont:

- de faptul ca Pamantul este curbat

- de razele de curbura

a.)     Calculul elemetelor preliminarii si reducerea observatiilor:

➢   (valoarea provizorie) pentru a reduce observatiile la suprafata considerata iar pentru directiileunghiulare zenitale trebuie sa calculam componenta deviatiei verticale in planul determinat de cele 2 puncte.

➢   Prin prelucrare se vor deduce corectii pentru masuratori si respectiv pentru altitudinile provizorii:

Δh_ij = Δh+ v_ij

H_i = H + dx_i

➢   Calculul coordonatelor punctelor din retea :

Folosindu-ne de latitudine si lobgitudine pe care le aproximam la fel ca in cazul nivelmentului geometric( transformarea coordonatelor geodezice B, L in coordonate rectactangulare X, Y in proiectia Stereografica 1970 (ΔB - 1' ≈ 30 m, ΔL - 1'≈ 20 m) calculam X si Y punctelor din retea.

Pentru punctul A vom alege o cota arbitrara care va ajuta la determianrea celorlalte puncte.

➢   Calculul orientarilor

Folosindu-ne de coordonatele punctelor, vom afla orientariile laturiilor , orientare ce ulterior va fi considerata egala cu azimutul.

b.) Reducerea distantelor :

b.1) Calculul diferentelor de nivel :

b.2 ) Reducerea distantei la coarda :

D_ij^c =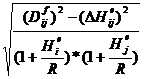

b.3) Reducerea distantei pe elipsoid :

s_ij =

b.4) Reducerea distantei la altitudinea medie :

D_ij = s_ij * ( 1 + H_m/R )

unde: H_m = - reprezinta altitudinea medie

c.)Formarea modelului functional-stochastic:

➢    Modelul Gauss-Markov:

v=Ax+l - modelul fuctional

unde:V - vectorul corectiilor

A - matricea coeficientilor sistemului de ecuatii ale corectilor

X - vectorul necunoscutelor

L - vectorul termenilor liberi

C_m=_o²Q_m - modelul stochastic

unde:C_m - reprezinta matricea de varianta -covarianta

Q_m matricea cofactorilor

_o - variatia unitatii de pondere

La formarea modelului functional stochastic trebuie sa se aiba in vedere urmatoarele:

-prelucrarea riguroasa a masuratorilor , sa se raporteze la un sistem unitar.

- orice modificare in modelul functional stochastic conduce la obtinerea altor rezultate.

- acest model functional stochastic poate fi imbunatatit pe baza unor rezultate obtinute intr-o prima prelucrare, prin analiza ponderilor grupelor de masuratori .

- conditia sub care se efectueaza prelucrarea prin metoda observatilor indirecte este:

V^TPV = minim

- cand cerintele de precizie nu sunt ridicate se mai poate face o aproximatie

V^TV = minim

Forma generala liniarizata a sistemului ecuatiilor de corectii este:

v_ij = a_ijx_i - a_ijx_j - b_ijy + l_ij ; p_ij

a_ij = b_ij =

l_ij =

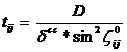
d.) Stabilirea ponderilor:

➢    In cazul nivelmentului geometric ponderea se calculeaza astfel: p =

➢    In cazul nivelmentului trigonometric ponderea se calculeaza astfel:p=

unde constanta se alege astfel incat ponderea sa fie in jurul valorii de 1.

e.) Normalizarea si rezolvarea sistemului normal:

- forma liniara

X=-N^-1 .A^{t .}P ^.L

unde:A - matricea coeficientilor sistemului liniarde ecuatii

P - reprezinta matricea ponderilor

N- matricea sistemului normal

x - matricea necunoscutelor sau solutziile sistemului de ecuatii

L - matricea termenilor liberi

I matricea unitate

f.)Calculul elementelor compensate:

(calculul valorilor cele mai probabile ale altitudinilor)

H_i = H + dx_i

ζ_ij = ζ_ij⁰ + v_ij (calculul distantelor zenitale)

k_i = k_i⁰ + y_i; k⁰ = 0,13 (control masuratorilor in functie de ultimu termen al matricei necunoscutelor)

g.) Calculul elementelor de precizie:

1.) abaterea standard a unitatzii de podere

[ ^cc/km]

unde :

m - reprezinta numarul de masuratori = 12

n - reprezinta numarul de necunoscute = 4

2.) Abaterea standard de determinare a unei masuratori compensate:

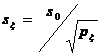
reprezinta ponderea diferentei de nivel pe tronsonul condiderat.

3.) abaterea standard de determinare a necunoscutelor:

qsunt elementele de pe diagonala principala a matricii inverse a sistemului normal

4.) abaterea medie standard pe retea :

Tabele

Transformarea coordonatelor geodezice (B,L)in coordinate plane (x,y) tinand cont de aproximatia

I. - 1.) Compensarea retelei de nivelment geometric - geodezic cu diferente de nivel masurate

Tabel 1.1 Calculul diferentelor de nivel provizorii

Tabel 1.2 Calculul cotelot provizorii

Tabel 1.3 Intocmirea sistemului normal al ecuatiilor de conditie

Tabel 1.4 Calculul altitudinilor comensate

Tabel 1.5 Calculul diferentelor de nivel compensate

Tabel 1.6 Controlul compensarii:

Calculul elementelor de precizie:

Tabel 1.7

Tabel 1.8

2). Compensarea retelei de nivelment geometric - geodezic in sistemul de altitudini ortometrice - sferoidice

Tabel 2.1 - Reducerea diferentelor de nivel la sistemul de altitudini ortometrice - sferoidic

Tabel 2.2 Diferente de nivel si distante pentru liniile de nivelment

Tabel 2.3 Forma sistemului liniar al ecuatiilor de corectie

Tabel 2.4 - Calculul altitudinilor compensate

Tabel 2.5 Calculul diferentelor de nivel compensate

Tabel 2.6 Controlul compensarii

Calculul elementelor de precizie:

Tabelul 2.7

Tabelul 2.8

3). Compensarea retelei de nivelment geometric - geodezic in sistemul de altitudini normale

T abel 3.1 - Reducerea diferentelor de nivel la sistemul de altitudini normale

Tabel 3.2 Diferente de nivel pentru liniile de nivelment

Tabel 3.3 Calculul altitudinilor provizorii pentru reperii de nivelment

Tabel 3.4 Forma sistemului liniar al ecuatiilor de corectii

Tabel 3.5 Calculul altitudinilor compensate

Tabel 3.6 Calculul diferentelor de nivel compensate

Tabel 3.7 Controlul compensarii

Calculul elementelor de precizie:

Tabelul 3.7

Tabelul 3.8

II. Prelucrarea masuratorilor efectuate in retele de nivelment trigonometric geodezic

Transformarea coordonatelor geodezice (B,L) in coordinate plane (x,y) tinand cont de aproximatia

Tabel 4.1 Coordonatele plane X si Y

Tabel 4.2 Calculul orintarilor intre reperii de nivelment trigonometric

Tabel 4.3 Calculul razei medii de curbura

Tabel 4. 4 Calculul diferentelor de nivel provizorii

Tabel 4. 5 Calculul cotelor provizorii

Tabel 4.6 Reducerea distantelor

Tabel 4.7 Calculu coeficientilor ecuatiilor de corectie

Tabel 4.8 Formarea sistemului liniar de ecuatii

Tabel 4.9 - Calculul directiilor zenitale compensate

Tabel 4.10 - Calculul altitudinilor compensate

Tabel 4.11 Controlul compensarii si prezentarea rezultatelor in urma compensarii

Calculul preciziilor :

Tabelul 4.12

Tabelul 4.13