Teorema unicitatii determinarii campului electromagnetic

Teorema unicitatii determinarii campului electromagnetic

Ecuatiile reprezentand legile generale ale campului electromagnetic macroscopic in medii fixe sau mobile si in domenii de continuitate si netezime a proprietatilor fizice locale, impreuna cu ecuatii de trecere (de pe suprafetele de discontinuitate electromagnetica si, eventual, asimetrica, sau pe curbele si in punctele singulare), determina in mod univoc structura (starea) si evolutia campului electromagnetic macroscopic, adica permit determinarea univoca a vectorilor de stare -locala si instantanee- a campului electromagnetic in teoria macroscopica: si , in oricare din regimurile sale, daca sunt precizate urmatoarele conditii (numite  conditii de unicitate):

1)   conditiile initiale (numai in regimul nestationar), prin care se cunosc marimile directe de stare a campului electromagnetic si , pentru orice punct P apartinand domeniului de existenta W, la momentul initial t = 0. Fata de sistemul de referinta atasat corpurilor, poate fi determinat prin raza sa vector care reprezinta distanta de la un punct de referinta (originea) la punctul P considerat, cu orientarea . In acest caz, conditiile initiale sunt si pentru si la t = t₀ = 0;

2)   conditiile la limita (pe suprafata ), care cuprind conditiile pe frontiera a domeniului camp W, ingloband si conditiile la infinit (daca domeniul camp W este infinit extins) in fiecare moment t > t₀ =0, a componentelor tangentiale sau pentru si la , precum si conditiile la interfata subdomeniilor de camp in medii neomogene;

3)   conditiile de material si starea corpurilor din camp, fixate prin ecuatiile constitutive corespunzatoare: ,, , , si . In general se presupune mediul liniar, izotrop si in repaus, deci caracterizat de marimile de material e m si g constante in timp;

4) conditiile de viteza (care sunt necesare numai in cazul unor medii mobile in camp) prin care se considera campul de viteze ca o distributie vectoriala cunoscuta pe W si intr-un interval de timp t = [0,T], cu derivatele partiale ale vitezei in raport cu coordonatele spatiale ca marimi scalare marginite;

5) conditiile de surse, care cer ca functiile de punct si de timp si sa fie cunoscute (date in domeniile de continuitate si netezime din W), ca si densitatea de suprafata a sarcinii electrice si densitatea de curent pe suprafetele de discontinuitate (electro-magnetica si, eventual, cinetica) existente in campul W

Aceasta formulare, evidentiata in esenta ei prin scrierea cursiva, reprezinta teorema de unicitate a campului electromagnetic in teoria sa macroscopica.

Teorema aceasta scoate in evidenta caracterul complet al legilor fundamentale ale teoriei macroscopice a campului electromagnetic, precum si caracterul obiectiv "cauza D efect" al campului electromagnetic (de a satisface principiul cauzabilitatii).

In formularea precedenta a teoremei de unicitate a campului electromagnetic s-a admis "a priori" existenta solutiei ecuatiilor fundamentale ale campului electromagnetic macroscopic - prin considerente matematice aplicate sistemului de ecuatii cu derivate partiale (1.105`) sau (1.105``). In tehnica, aceasta existenta a unicitatii este probata "a posteriori", de elaborarea -prin aplicarea conditiilor de unicitate (formulate anterior)- a solutiei cautate.

In tratatul Preda, M., Cristea, P., Spinei, F., 1980 se prezinta o demonstartie eleganta -prin reducerea la absurd- a teoremei de unicitate a campului electromagnetic, considerandu-se cazul particular -mai simplu- al unui mediu liniar, izotrop si in repaus, ceea ce implica numai conditiile de unicitate 1), 2) si 3) ale teoremei.

Se presupune, prin reducere la absurd, ca ecuatiile generale ale legilor campului electromagnetic, in conditiile de unicitate 1), 2) si 3), ar conduce la doua solutii si anume:

si

. (U1)

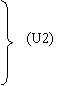Fiind solutii, aceste marimi satisfac -ambele- legile campului electromagnetic pentru medii izotrope, liniare si in repaus, ceea ce inseamna ca se poate scrie:

si ,

si ,

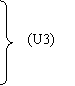adica primele doua ecuatii de baza ale lui Maxwell (1.105), precum si legile de material (in aceleasi conditii de material 3):

si ,

si ,

si ,

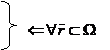care indeplinesc aceleasi conditii initiale 1), ceea ce inseamna ca se poate scrie:

si aceleasi conditii la limita, componentele tangentiale la fiind:

.

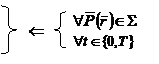
Diferentele celor doua solutii, adica:

si , (U6)

trebuie sa satisfaca si ele sistemul de ecuatii (1.105) si (1.106), putandu-se scrie:

, (1)

, (3)

, (4)

, (5)

obtinut prin scaderea, membru cu membru, a expresiilor (U2) si (U3).

Avand in vedere relatiile (U4) si (U5), rezulta: conditiile initiale (U4) si cele pe frontiera (U5) ale marimilor diferenta sunt conditii de zero, adica:

si:

Puterea disipata P_d in mediul din campul W, cu volumul v_W, de sistemul de marimi diferenta (U6) este - conform legii tarnsformarii de energie (1.102``) si (1.103``):

,

care prin inlocuirea lui rezultat din relatia (2) a sistemului (U7), devine:

(U10)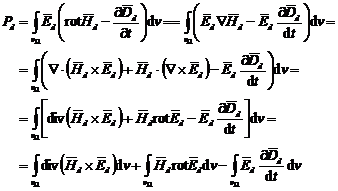

In membrul drept al relatiei (U10) se pot face urmatoarele inlocuiri:

- aplicandu-se formula lui Gauss-Ostrogradski (9.20) - v.§ 9.1.2 primului termen rezulta:

;

- inlocuindu-se in termenul al doilea rot prin expresia sa (1) din sistemul (U7) si inlocuindu-se cu expresia sa (5) din (U7) rezulta:

;

- inlocuindu-se in ultimul termen cu expresia sa (4) din sistemul (U7) rezulta:

,

astfel ca relatia (U10) devine:

(U11)

deoarece in conditiile pe frontiera (U9) produsul vectorial si atunci:

,

care, prin inlocuirea lui cu expresia sa (3) din sistemul (U7), devine:

(U12)     .

Membrul stang al egalitatii (U12) este, intotdeauna in intervalul [0, T] si peste tot in W, nenegativ - deoarece g > 0 si ; aceasta are implicatia: derivata integralei din membrul drept (U12) trebuie sa fie (este) negativa, ceea ce inseamna ca integrala derivata este sau scazatoare sau constanta. Dar, conform conditiilor initiale (U8), la momentul initial , integrala din membrul drept al egalitatii (U12) fiind nula, rezulta ca la orice alt timp aceasta integrala este ori nenegativa ori nula; insa cum fiecare termen al integralei este sigur nenegativ (deoarece simultan si peste tot in W si ), atunci ea este nula in . Prin urmare:

si, de aici:

si ,

iar -conform expresiilor (3), (4) si (5) din (U7)- atunci si celelalte marimi vectoriale diferenta sunt nule; adica:

si .

In acest fel, toate ecuatiile (U6) sunt nule si deci cele doua solutii (U1), presupuse initial ca fiind diferite, sunt identice: si , peste tot (in orice domeniu W) si oricand in timp. In acest fel, teorema de unicitate a campului electromagnetic, formulata la inceputul acestui paragraf, este demonstrata, cel putin pentru cazul particular al unui mediu izotop si liniar aflat in repaus, in conditiile de unicitate 1), 2) si 3).