
|
|
|
Reprezentarile graficele sunt forme intuitive de prezentare a distributiilor de frecvente ("o imagine face mai mult decat o mie de cuvinte"). Ele sunt foarte frecvent utilizate pentru analiza si prezentarea datelor in psihologia aplicata deoarece faciliteaza intelegerea semnificatiei datelor numerice. In prezent, programele computerizate ofera mijloace extrem de puternice si de sofisticate pentru elaborarea reprezentarilor grafice. Dar simpla utilizare a unui astfel de program nu garanteaza realizarea unui grafic eficient. In esenta, un grafic eficient este o combinatie reusita intre forma si continutul statistic pe care il reflecta. Realizarea acestei combinatii depinde de respectarea catorva principii esentiale:
Formele de expresie grafica a datelor statistice sunt foarte numeroase. Ne vom ocupa aici doar de cateva dintre acestea, cel mai des utilizate[1][1]:
graficul de tip bara
histograma
poligonul de frecvente
graficul frecventei cumulate
graficul circular
graficul de tip "stem and leaf" ("tulpina si frunze")
In cele ce urmeaza, vom face o trecere sumara in revista a celor mai utilizate tipuri de reprezentari grafice.
Este cel mai simplu mod de reprezentare grafica a datelor. Se utilizeaza atunci cand dorim sa reprezentam o variabila "discreta" (care prezinta valori intregi, de exemplu, numarul de raspunsuri corecte la un test in functie de nivelul de instruire al subiectilor).
In mod obisnuit, un grafic se prezinta ca o imagine inclusa intr-un sistem de axe perpendiculare:
Iata cum arata un grafic de acest tip efectuat pe datele din tabelul de frecvente grupate, luand clasele drept valori ale distributiei. Cu cat frecventa unei valori este mai mare, cu atat bara este mai mare. Simplitatea si claritatea este cea mai mare calitate a acestui tip de grafic.
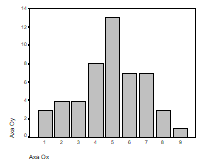
Observatii:
Toate barele trebuie sa aiba aceeasi latime
Intre bare se lasa un spatiu (deoarece nu exista nici o legatura intre ceea ce reprezinta ele)
Barele pot fi puse in orice ordine. Ordonarea barelor, descrescator sau crescator, creeaza un grafic-bara special, numit grafic Pareto.
La prima vedere, histograma este asemanatoare cu graficul de tip bara. Ea este adecvata pentru situatiile cand variabila pe care dorim sa o reprezentam este de tip "continuu" (adica poate lua orice valoare pe o scala numerica, de ex., numar de raspunsuri corecte, timpul de reactie, lungimea, etc.). Iata, de exemplu, histograma distributiei de frecvente din tabelul 3 (realizata cu programul SPSS):
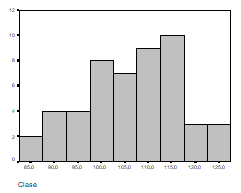
Se observa faptul ca programul a realizat automat o grupare de frecvente, afisand pe axa Ox limita minima a intervalului ca "eticheta" a acestuia.
Este o reprezentare alternativa la histograma. Punctele centrale ale suprafetelor rectangulare care reprezinta frecventa sunt unite cu o linie care delimiteaza suprafata poligonului.
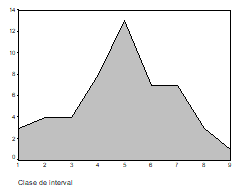
Imaginea prezinta distributia de frecvente grupate din tabelul de mai sus, cifrele 1,2,3,4,5,6,7,8,9 reprezentand denumirea conventionala a fiecarei clase.
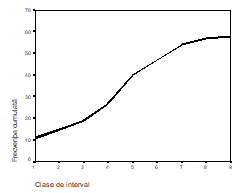
Este un grafic de tip liniar care reprezinta valorile frecventei absolute cumulate. Pe acest grafic se vede cu usurinta cate valori se afla pana la o anumita valoare din distributie (datele reprezentate sunt cele din tabelul 3, fiecare interval de clasa fiind etichetat conventional cu cifre de la 1 la 9).
Este utilizat in situatiile in care valorile sunt "parte a unui intreg". De exemplu, poate fi utilizat la reprezentarea distributiei de frecvente grupate de mai sus, pentru a avea o imagine directa a ponderii frecventei fiecarei clase de interval in raport cu celelalte.
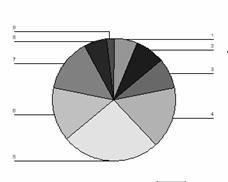
Graficul reprezinta frecventa absoluta a claselor de interval ale aceleiasi distributii de mai sus. Pe un grafic de acest tip se pot reprezenta fie valorile absolute, fie procentajul fiecarei clase raportat la intreg.
Este o reprezentare care incearca sa imbine expresia numerica cu cea grafica, fiind propusa de statisticianul J.W. Tuckey (1977). Scopul principal a fost acela de a oferi nu doar o imagine a distributiei ci si o metoda de explorare a acesteia. Ea este din ce in ce mai utilizata de psihologi, motiv pentru care consideram necesar sa o prezentam aici.
Atunci cand utilizam o distributie de frecvente grupate, cazurile individuale "se pierd" la nivelul fiecarei clase de interval fara a mai putea sti unde se plaseaza fiecare valoare initiala in interiorul fiecarui interval. Reprezentarea de tip stem-and-leaf (pe scurt stem plot), are tocmai avantajul de a realiza graficul distributiei cu pastrarea valorilor individuale.
Modul de realizare
Sa revenim la distributia prezentata anterior:
101
94
87
117
115
116
91
113
96
105
92
107
118
114
98
112
101
114
107
109
97
109
124
102
118
113
116
106
108
89
106
108
115
92
97
102
108
102
109
114
107
104
110
101
101
121
125
86
109
123
Mai intai, observam ca valorile sunt cuprinse intre 86 si 125. Alegem o valoare convenabila pentru tulpina, care va juca rolul de interval de clasa, care in cazul nostru poate fi 10. "Tulpina" reprezentarii stem plot este in acest caz numarul de zeci din fiecare valoare individuala.

Valorile din coloana stem indica numarul de zeci, iar cele din coloana Leaf, numarul de unitati. Daca privim imaginea in ansamblu ne-o putem reprezenta ca pe o histograma orizontala. In acest exemplu:
Stem 8, urmat de Leaf 679 indica faptul ca variabila noastra are in compunere valorile 86,87,89.
Stem 12, urmat de leaf 134, ne arata ca distributia contine valorile 121, 123,124
Concluzii.
Utilizarea tabelelor de frecventa si a reprezentarilor grafice aduce un important castig in analiza datelor statistice. Este insa, important sa retinem faptul ca atat tabele cat si reprezentarile grafice nu sunt decat inceputul analizei datelor nu si sfarsitul acesteia. Cu alte cuvinte, nu vom putea trage direct concluzii pe baza lor. Ele pot fi utilizate, insa, pentru a ilustra concluzii, care devin astfel mai usor de inteles si de retinut. In fazele primare de analiza a datelor statistice, graficele ne ajuta sa ne facem o imagine generala asupra acestora, lucru util pentru alegerea procedurilor statistice. Este important sa alegem tipul de grafic adecvat in raport cu natura datelor si cu ideea pe care dorim sa o ilustram. In practica, graficele se realizeaza utilizand programe specializate, iar SPSS are proceduri puternice de realizare a unei largi varietati de grafice.
TEMA PENTRU ACASA
Valorile de mai jos reprezinta distributia rezultatelor la un test de calcul aritmetic (numarul de calcule corecte)
Scor
Scor
Scor
Scor
Scor
55
30
52
49
54
46
53
54
50
59
52
57
48
45
49
51
62
46
33
42
48
39
47
50
56
50
68
44
51
53
Realizati:
1. Tabelul frecventelor simple
2. Indicati:
scorul cel mai frecvent
ce procent de valori se afla sub scorul 33
valoarea (scorul) ce mai apropiata de percentila 20
3. Tabelul frecventelor grupate (indicati modul de alegere a numarului de intervale, marimea intervalului de clasa, intervalele de clasa, frecventa simpla, relativa si cumulata a grupelor de frecventa)
4. Reprezentarea grafica de tip stem-and-leaf
Asa cum am vazut, analiza de frecvente este o metoda utila pentru punerea in valoare a unor caracteristici ale distributiilor statistice. Cu toate acestea, ea este tributara necesitatii de a manipula intreaga cantitate de date, toate valorile unei distributii (fie ele si grupate). Pentru a elimina acest neajuns sunt utilizati asa numitii indicatori sintetici. Acestia sunt descriptori numerici care condenseaza intr-o valoare unica o anumita caracteristica a unei intregi distributii de valori. Principalele avantaje pe care le ofera sunt concentrarea semnificatiei si usurinta utilizarii. In acelasi timp, insa, trebuie sa avem in vedere ca, prin natura lor sintetica, fiecare indicator pierde o anumita cantitate de informatie care tine de alte caracteristici, pe care nu le surprinde.
Tipuri de indicatori sintetici:
Trei sunt caracteristicile distributiilor care sunt evaluate cu ajutorul indicatorilor sintetici: tendinta centrala, variabilitatea (imprastierea, diversitatea), forma distributiei. Pentru fiecare din aceste caracteristici se utilizeaza anumiti indicatori specifici:
Indicatori ai tendintei centrale: Acestia sunt valori tipice, reprezentative, care descriu distributia in intregul ei;
Indicatori ai variabilitatii: Sunt valori care descriu caracteristica de imprastiere a distributiei. O distributie care contine aceeasi valoare, ori de cate ori s-ar repeta ea, are o variabilitate zero.
Indicatori ai formei distributiei: Sunt valori care se refera la forma curbei de reprezentare grafica a distributiei, prin comparatie cu o curba normala (oblicitate, aplatizare)
Este expresia ce mai directa a valorii tipice (reprezentative)
In cazul unei distributii simple, este valoarea cu frecventa cea mai mare de aparitie
In cazul unei distributii de frecvente grupate, este clasa de interval cu frecventa cea mai mare de aparitie
Se afla prin alcatuirea tabelei de frecvente (simple sau grupate) si este valoarea careia ii corespunde frecventa absoluta cea mai ridicata.
Distributiile pot avea un singur mod (unimodale), doua moduri (bimodale) sau mai multe (multimodale)
Exemplu: In seria de valori 5,8,3,2,5,4, Mo=5 (apare de cele mai multe ori)
Este valoarea "din mijlocul" unei distributii, adica aceea care are 50% dintre valori deasupra ei si 50% dintre valori dedesubtul ei (cu alte cuvinte, percentila 50).
Se gaseste prin alcatuirea tabelei de frecvente, in coloana frecventelor relative procentuale cumulate, si corespunde valorii de 50%.
In cazul distributiilor cu numar impar de valori, Me este chiar valoarea respectiva.
In cazul distributiilor pare, Me se calculeaza ca medie a celor doua valori din mijlocul distributiei
Exemplu:
In seria de valori 5,8,3,2,5,4, ordonata crescator (2,3,4,5,5,8), Me=4,5 (ca medie a valorilor 4 si 5 aflate in mijlocul unei distributii pare). Daca distributia noastra ar fi avut 5 valori (fara 2, de exemplu), Me=5
Este raportul dintre suma valorilor distributiei si numarul acestora
Notatii uzuale:
o m (miu), atunci cand este media intregii populatii de referinta
o m, atunci cand se calculeaza pentru un esantion (cazul cel mai frecvent)
Calcularea mediei pentru o distributie simpla de frecvente se face prin adunarea valorilor si se impartirea la numarul lor
o Exemplu: Pentru distributia 5,8,3,2,5,4
![]() (formula
2.1)
(formula
2.1)
Calcularea mediei pentru o distributie de frecvente grupate: Se face suma produsului dintre fiecare valoare si frecventa ei, apoi se imparte la suma frecventelor (numarul valorilor)
Exemplu: Pentru distributia: 5,8,3,3,3,2,4,2,3,5,4
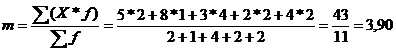 (formula
2.2)
(formula
2.2)
NOTA: In expresia de mai sus:
X este variabila. ![]() se
intelege ca "Suma de la X=1 la N (numarul valorilor)
se
intelege ca "Suma de la X=1 la N (numarul valorilor)![]()
f este frecventa . ![]() se intelege ca "Suma de la f=1 la
k (unde k numarul grupelor de frecventa)
se intelege ca "Suma de la f=1 la
k (unde k numarul grupelor de frecventa)
Proprietatile mediei aritmetice
o Adaugareascaderea unei constante la fiecare valoare a distributiei, marestescade media cu acea valoare
o Inmultireaimpartirea fiecarei valori a distributiei cu o constanta, multiplicadivide media cu acea constanta
o Suma abaterii valorilor de la medie este intotdeauna egala cu zero
o Suma patratului abaterilor de la medie va fi intotdeauna mai mica decat suma patratelor abaterilor in raport cu oricare alt punct al distributiei
Avantajele si dezavantajele indicatorilor tendintei centrale
Tabloul de mai jos prezinta, in mod sintetic avantajele si dezavantajele specifice indicatorilor tendintei centrale:
AVANTAJE
DEZAVANTAJE
MODUL
- Usor de calculat (nesemnificativ in prezent);
- Poate fi utilizat pentru orice tip de scala;
- Este singurul indicator pentru scale nominale;-
- Corespunde unui scor real al distributiei;
- In general, nesigur, mai ales in cazul esantioanelor mici, cand se poate modifica dramatic la o modificare minora a unei valori;
- Poate fi gresit interpretat. Se identifica total cu un scor anume, fara a spune nimic despre celelalte valori;
- Nu poate fi utilizat in statistici inferentiale;
MEDIANA
- Poate fi utilizata pe scale ordinale si de intervalraport;
- Poate fi utilizata si pe distributii de frecventa cu clase deschise sau scoruri nedeterminate la marginile distributiei;
- Poate sa nu corespunda unei valori reale (N par);
- Nu reflecta valorile distributiei (un scor extrem se poate modifica, fara a afecta Me);
- Este mai putin sigura in extrapolarea de la esantion la populatie;
- Greu de utilizat in statistici avansate
MEDIA
- Reflecta valorile intregii distributii;
- Are multe proprietati statistice dezirabile;
- Adecvata pentru utilizare in statistici avansate;
- De obicei nu corespunde unei valori reale;
- Nu este tocmai adecvata pentru scale ordinale;
- Conduce la interpretari gresite pe distributii asimetrice
- Poate fi puternic afectata de scorurile extreme;
Valorile extreme reprezinta valori excesive, neobisnuit de mari sau de mici fata de celelalte valori ale unei distributii. Identificarea lor este necesara pentru a evita efectul pe care il au asupra valorilor tendintei centrale, in primul rand asupra mediei. Una dintre metodele de identificare este analiza grafica de tip Box-and-Whisker-Plot (pe scurt Box-Plot), elaborata de Tukey.
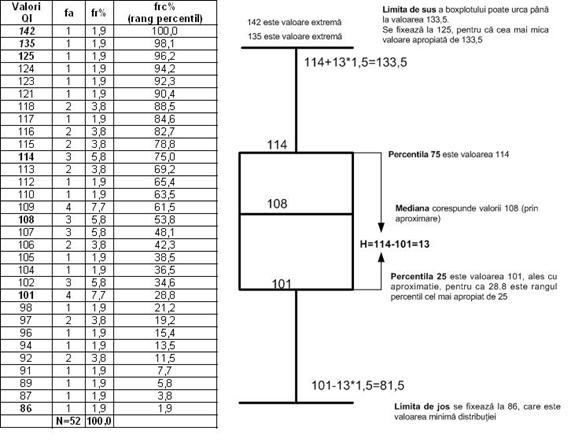
In esenta, reprezentarea Box-Plot (vezi imaginea) este constituita dintr-o caseta (dreptunghi), a carui limita inferioara este plasata in dreptul percentilei 25, limita superioara fiind plasata in dreptul percentilei 75. Cu alte cuvinte, caseta cuprinde 50% dintre valorile unei distributii. Distanta dintre valorile limita ale casetei se numeste H.
Linia din interiorul casetei marcheaza valoarea mediana (Me)
"Mustatile" care pornesc de la limita superioara si inferioara a casetei, au o lungime maxima egala cu 1,5 H. In acel punct se plaseaza ultima valoare "legitima" a distributiei. Orice valoare mai mica sau mai mare de acestea, sunt definite ca extreme (Outliers)
Un exemplu de creare a reprezentarii box plot: Vom utiliza distributia scorurilor QI prezentata anterior, la care am adaugat doua valori suplimentare (135 si 142), alese intentionat pentru a fi mai mari decat restul valorilor.
101
94
87
117
115
116
91
113
96
105
135
92
107
118
114
98
112
101
114
107
109
142
97
109
124
102
118
113
116
106
108
89
106
108
115
92
97
102
108
102
109
114
107
104
110
101
101
121
125
86
109
123
Pentru a face reprezentarea box plot facem mai intai tabela de frecvente simple, cu scopul calcularii percentilelor. Tabelul de frecvente alaturat cuprinde valorile ordonate ale distributiei, intre de la valoarea cea mai mica (86) si se cea mai mare (142). Pe coloana frc% se afla frecventele cumulate procentuale (percentilele). Pentru box plot identificam percentilele 25 si 75. Ele corespund valorilor 101 (este valoarea cea mai apropiata de 25 pe coloana frc%) si, respectiv, 114. Am obtinut astfel, limita inferioara si superioara a casetei. Mediana (percentila 50) corespunde valorii 108 (frc%=53.8, prin aproximare). Diferenta dintre valorile corespunzatoare percentilelor 25 si 50 este 13 (114-101). Astfel putem determina limitele prelungirilor superioara si inferioara ale casetei care sunt: 114+13*1.5=128 (aproximare) pentru prelungirea superioara si, respectiv 101-13*1,5=83 (aproximare) pentru cea de jos. Am obtinut astfel toate valorile necesare trasarii box plotului.
Imaginea de mai jos prezinta tabelul distributiei si boxplotul corespunzator[2][1]:
Tratarea valorilor extreme
Punerea in evidenta a unor valori extreme ridica problema modului lor de tratare a acestor valori. In acest scop, trebuie sa avem in vedere doua aspecte:
1. Stabilirea naturii valorilor extreme, care pot fi:
a. erori de inregistrare (tastare);
b. erori de masurare;
c. rezultate influentate de anomalii ale conditiilor experimentale.
d. Esantionul a fost extras dintr-o populatie asimetrica
e. Valorile respective fac parte din alta populatie de valori
f. Esantion prea mic
2. Tratarea lor pe una din caile posibile:
a. eliminare (daca sunt erori necorectabile);
b. corectare (daca este posibil);
c. utilizarea mediei 5%trim, adica a mediei care nu tine cont de 5% din numarul valorilor de la fiecare din cele doua extremitati ale distributiei.
d. transformare (daca datele sunt corecte si, totusi, dorim sa evitam efectul lor asupra indicatorilor sintetici). Exista diverse metode de transformare: extragerea radicalului din toate valorile distributiei, logaritmarea distributiei, etc.[3][2]
Analiza valorile extreme reprezinta unul dintre obiectivele principale ale fazelor preliminare de analiza a datelor. Prezenta lor este de natura sa aiba efecte majore asupra rezultatelor fapt care trebuie luat in considerare la alegerea procedurilor statistice inferentiale.
Valori nedeterminate si clase deschise
Valorile "nedeterminate" sunt acele valori a caror marime nu decurge din procesul de masurare, in acelasi mod in care rezulta oricare valoare a seriei (Exemplu: La testul de asociere verbala, daca subiectul depaseste, sa zicem 10 sec., se inregistreaza valoarea 10, fara a se astepta, la infinit (?), un raspuns). Categorii "deschise" sunt acele categorii de valori care au una dintre limite "libera" (Exemplu: Cate tigari fumezi zilnic? Se poate inregistra numarul tigarilor ca atare, dar ultima valoare este "30 sau mai mult).
In ambele situatii de mai sus, utilizarea mediei este nesigura (si incorecta). Indicatorul recomandabil este mediana.
[1][1] In mod normal, reprezentarea boxplot se construieste independent de tabelul de frecvente. Daca le-am asociat in imaginea de mai sus, am facut-o doar cu scop didactic, pentru a pune mai clar in evidenta mecanismul de elaborare
[1][2] Aceste metode vor fi discutate cu ocazia aplicatiilor SPSS.
Indicatorii tendintei centrale se refera la ceea ce face ca valorile sa se asemene, la caracteristica "comuna" a valorilor unei distributii. Indicatorii imprastierii, de care vom vorbi in continuare, se refera la caracteristica de variabilitate, care descrie diferentele existente intre valori. In cazul tendintei centrale este scoasa in evidenta caracteristica valorilor unei distributii de a se "asemana" unele cu altele, "asemanare" surprinsa de indicatorii tendintei centrale. In cazul imprastierii, se urmareste descrierea tendintei valorilor de a se deosebi una de alta, de a se "sustrage" unei tendinte centrale prin indepartarea de aceasta. De exemplu, o distributie de tipul 2,2,2,2,2,2,2 este, evident, mult mai omogena (mai putin variabila) decat o distributie de genul 1,2,3,4,5,6,7.
De fapt, prima din cele doua serii de valori nu prezinta nici o variatie, toate valorile fiind identice unele cu celelalte. Intr-o serie de valori identice, reprezentativitatea unui indicator al tendintei centrale este absoluta (Mo=Me=m=Xi, unde Xi este fiecare dintre valorile distributiei). Acesta este un caz extrem si improbabil. Intr-o distributie reala fiecare valoare are "individualitatea" ei. Cu cat valorile difera mai mult una de alta, cu atat variabilitatea distributiei este mai mare. O definitie echivalenta, care este mai usor de tradus in operatii matematice, priveste variabilitatea ca masura in care valorile difera fata de medie.
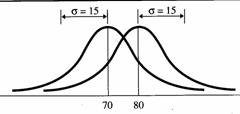
Sa ne imaginam urmatoarea situatie: Un psiholog clinician vrea sa vada efectul unei metode de crestere a increderii in sine pe un lot de subiecti. In acest scop, el evalueaza increderea in sine inainte si dupa sedintele de psihoterapie. Distributia valorilor este reprezentata in imaginea de mai jos:
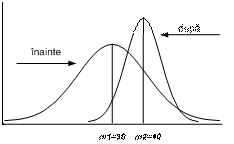
Asa cum se observa, valorile increderii masurate inainte de cura psihoterapeutica au o medie de 30 si o imprastiere (neomogenitate) mai mare, in timp ce valorile de dupa tratament prezinta o medie de 40 si o imprastiere mai mica, (sunt mai omogene). Acest fapt sugereaza ca tratamentul psihoterapeutic a avut efect[4][1]. Imaginea scoate in evidenta si faptul ca in distributiile mai omogene media este mai reprezentativa decat in distributiile mai putin omogene.
Pentru evaluarea imprastierii distributiilor statistice se utilizeaza mai multi indicatori. Distingem doua categorii de indicatori ai imprastierii: elementari si sintetici.
Principala caracteristica a indicatorilor elementari este aceea ca surprind imprastierea distributiei prin distanta dintre doar doua valori ale acesteia.
Este data de diferenta dintre valoarea maxima si valoarea minima a unei distributii
R=Xmax-Xmin (formula 2.3)
Utilitatea ei este data de faptul ca ne indica in mod absolut plaja de valori intre care se intinde distributia.
Principalul dezavantaj consta in faptul ca poate fi influentata de o singura valoare aflata la extremitatea distributiei.
Este data de raportul procentual dintre amplitudinea absoluta si media distributiei:
![]() (formula 2.4)
(formula 2.4)
Este utila atunci cand cunoastem plaja teoretica de variatie a distributiei, putand astfel sa facem o comparatie cu plaja reala, obtinuta prin formula de mai sus.
Din cauza ca amplitudinea utilizeaza doar cele doua valori extreme ale distributiei, este un indicator imprecise al variabilitatii:
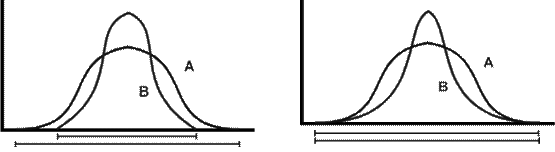 Exemple:
Exemple:
Distributia A are o amplitudine mai mare dar si o variabilitate mai mare decat distributia B
Amplitudinea distributiilor A si B sunt identice, dar distributia A are mai multa variabilitate.
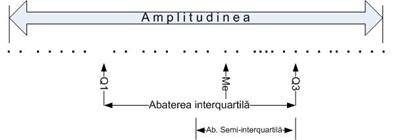
Quartilele (Q) sunt percentilele care impart distributia in patru segmente egale. Ele sunt: Q1 (percentila 25); Q2 (percentila 50, sau Me); Q3 (percentila 75).
Abaterea quartila este data de diferenta dintre valoarea corespunzatoare quartilei 3 si valoarea corespunzatoare quartilei 1
![]() (formula
2.5)
(formula
2.5)
Nota bene: Se poate observa ca este chiar distanta dintre limita superioara si cea inferioara a casetei Box-Plot (valoarea H)
Semnifica distanta unui un scor "tipic" fata de amplitudinea intregii distributii si se calculeaza ca media diferentei dintre quartila 3 si quartila 1.
![]() (Formula
2.6)
(Formula
2.6)
Intr-o distributie perfect simetrica RSQ=Q2=Me
RSQ nu este afectata de valorile aberante fiind considerata, din acest motiv, un indicator "robust" al imprastierii
O imagine de ansamblu a tipurilor de indicatori elementari ai imprastierii ne este data de figura de mai jos, unde am figurat prin puncte o distributie oarecare de 31 de valori posibile.
Asa cum am precizat, acest tip de indicatori ilustreaza imprastierea prin distanta dintre doua puncte ale unei distributii. Unul dintre avantajele lor este acela al usurintei de calcul. Pe de alta parte, tocmai pentru ca iau in seama doar doua dintre valorile distributiei, sunt vulnerabili si nesiguri. Utilitatea lor este in general limitata dar sunt singurii care pot fi folositi atunci cand indicatorii sintetici (de care vom vorbi in continuare), nu pot fi calculati. Un alt dezavantaj al acestora este dificultatea de a fi utilizati in procedurile statistice avansate.
Spre deosebire de indicatorii elementari, indicatorii sintetici surprind imprastierea unei distributii prin luarea in considerarea abaterii fiecarei valori de la un anumit indicator al tendintei centrale. Cel mai uzual indicator de referinta pentru imprastiere este media. Aceasta pentru ca, asa cum ne amintim, media are avantajul de a fi o "concentrare" a tuturor valorilor unei distributii.
Distanta dintre o valoare anumita si media distributiei se numeste abaterea valorii (Xi-m). Daca am dori sa calculam abaterea medie a unei distributii nu ne-ar ramane decat sa insumam abaterile individuale ale fiecarei valori si sa le impartim la numarul acestora. Din pacate, media abaterilor intr-o distributie este intotdeauna egala cu zero (vezi proprietatile mediei). Acest fapt poate fi descris cu formula
![]()
unde Xi sunt valorile distributiei, m este media iar N, numarul de valori, si poate fi pus in evidenta practic, astfel:
X
Xi - m
5
(5 - 4.5) = .5
8
(8 - 4.5) =3.5
3
(3 - 4.5) = -1.5
2
(2 - 4.5) = -2.5
5
(5 - 4.5) = .5
4
(4 - 4.5) = -.5
SX = 27
S(Xi-m) = 0
N = 6
m = 4.5
Asa cum se observa in coloana "Xi-m", diferentele individuale insumate produc S(Xi-m) = 0. Acest lucru este valabil pentru orice fel de distributie si este una dintre proprietatile importante ale mediei.
Pentru a elimina acest inconvenient putem sa luam abaterile individuale in valoare absoluta (fara semn).
X
(Xi - m)
5
(5 - 4.5) =.5
8
(8 - 4.5) = 3.5
3
(3 - 4.5) = 1.5
2
(2 - 4.5) = 2.5
5
(5 - 4.5) =.5
4
(4 - 4.5) =.5
SX = 27
S|Xi-m| = 9
N = 6
m = 4.5
Ca urmare, formula abaterii medii (d) poate fi scrisa astfel:
![]() (formula
2.7)
(formula
2.7)
Pentru cazul frecventelor grupate, formula devine:
![]()
(Formula 2.8)
Abaterea medie este usor de inteles si are semnificatia de medie a distantelor intre fiecare scor si media distributiei. Din pacate, nici ea nu este potrivita cu statisticile avansate
Notatii uzuale:
s2 (cand se calculeaza pentru esantion)
s2 (cand se calculeaza pentru intreaga populatie)
Pentru a elimina inconvenientul abaterilor de la medie de a avea suma egala cu zero, se opereaza ridicarea la patrat a abaterilor valorilor individuale[6][3]
X
(Xi - m)
(Xi - m) 2
5
(5 - 4.5) = .5
.25
8
(8 - 4.5) =3.5
12.25
3
(3 - 4.5) = -1.5
2.25
2
(2 - 4.5) = -2.5
6.25
5
(5 - 4.5) = .5
.25
4
(4 - 4.5) = -.5
.25
SX = 27
S(Xi-m) = 0
S(X-m)2 = 21.5
N = 6
M = 4.5
Daca insumam abaterile ridicate la patrat (patratice) si le impartim la numarul valorilor, obtinem dispersia (numita si varianta sau abatere medie patratica)
![]() (formula 2.9)
(formula 2.9)
Nota: Formula contine la numitor o anumita inexactitate care va fi discutata mai departe (vezi formula 2.11)
Totusi, din cauza ridicarii la patrat, dispersia nu reprezinta o valoare foarte buna a imprastierii (de ex., poate fi mai mare decat amplitudinea distributiei). Solutia acestui neajuns o constituie:
Notatii uzuale:
s (pentru esantioane)
s (pentru populatie)
SD (Standard Deviation, in standardul APA )
ab.std.
Abaterea standard se obtine prin extragerea radicalului din expresia abaterii medii patratice (dispersiei).
Formula
de calcul: ![]() (formula 2.10)
(formula 2.10)
NOTA: Formula contine o inexactitate la numitor care va fi discutata mai departe (vezi formula 2.11)
Pe
datele din tabelul de mai sus: ![]()
Operatiile succesive efectuate mai sus, ridicarea la patrat si extragerea radicalului, nu trebuie vazute ca operatii artificiale, "gratuite". Aceste operatii nu se refera la valorile distributiei ci la abaterile de la medie, ceea ce conduce la rezultate diferite care exprima, intr-o alta forma, aceeasi caracteristica de imprastiere a valorilor originale.
Corectia indicatorilor imprastierii calculati pentru esantioane
Formulele 2.8 si 2.9 au la numitor valoarea N (volumul esantionului). Fara a intra in detalii, vom spune ca valorile astfel calculate, ale dispersiei si abaterii standard, pentru un esantion, contin o imprecizie (bias) care conduce la subestimarea imprastierea la nivelul populatiei. Chiar daca luam in considerare un numar mare de esantioane, extrase succesiv dintr-o anumita populatie, indicatorii imprastierii vor fi mai mici decat imprastierea la nivelul intregii populatii.
Corectia se face prin utilizarea la numitor a expresiei N-1. In acest mod, cu cat esantionul este mai mic, cu atat indicatorul respectiv al imprastierii va fi influentat mai mult de expresia de la numitor.
Expresia N-1 poarta numele de "grade de libertate". Pentru a-i intelege semnificatia, este bine sa ne gandim la faptul ca, intr-o distributie de 3 valori (de exemplu: 1,3,8) media este 4, iar abaterile de la medie sunt -3, -1, 4. Suma lor este zero. Ca urmare, este suficient sa cunoastem cel putin doua din cele trei valori pentru a o afla pe a treia. Altfel spus, doar doua valori sunt libere sa se modifice, a treia (ultima) fiind determinata de acestea.
Formulele corecte devin:
Dispersia:![]() (formula
2.11)
(formula
2.11)
Abaterea standard: ![]() (formula 2.12)
(formula 2.12)
Formulele initiale, de definitie, raman corecte pentru situatia in care se urmareste doar descrierea caracteristicii de imprastiere pentru esantionul respectiv. Atunci cand se urmareste insa, extrapolarea acestei valori la nivelul populatiei, utilizarea formulei corectate este absolut necesara. Este evident ca diferenta dintre valoarea corectata si cea necorectata a variabilitatii este cu atat mai mare cu cat esantionul este mai mic, ponderea numitorului asupra rezultatului fiind astfel mai mare. Cu cat N este mai mare, rezultatul formulei este mai putin afectat de diferenta de o unitate a numitorului. Programele de prelucrari statistice utilizeaza pentru calculul celor doi indicatori doar formulele corectate.
Proprietatile abaterii standard
Abaterea standard este, asa cum vom vedea, indicatorul principal al imprastierii utilizat in diverse proceduri statistice avansate. Pentru a-i justifica modul de utilizare in diverse formule, trebuie sa retinem cateva proprietati fundamentale ale abaterii standard:
 1. Daca se adauga/scade o constanta
la fiecare valoare a unei distributii, abaterea standard nu este
afectata
1. Daca se adauga/scade o constanta
la fiecare valoare a unei distributii, abaterea standard nu este
afectata
2. Daca se multiplica/divide fiecare valoare a unei distributii cu o constanta, abaterea standard se multiplica/divide cu acea constanta
3. Abaterea standard fata de medie este mai mica decat abaterea standard fata de orice alta valoare a unei distributii
Abaterea medie si abaterea standard se exprima in unitatile de masura ale variabilei de referinta. De exemplu, pentru o distributie de timpi de reactie, exprimati in sutimi de secunda, s=2.14 inseamna ca imprastierea standard este de 2.14 sutimi de secunda.
Daca acelasi esantion face si un test de coordonare a miscarilor, evaluat in numar de "iesiri din traseu" a caror abatere standard este s=20.94, nu putem compara omogenitatea celor doua serii de valori. Adica, nu putem spune daca esantionul este mai omogen sau mai putin omogen din perspectiva unei dintre cele doua performante.
Dintre solutiile posibile pentru eliminarea acestui neajuns, cea mai des utilizata este coeficientul de variatie (variabilitate), notat cu cv (sau v), propus de Pearson. Se calculeaza ca raport intre abaterea standard si medie. Poate fi exprimat si procentual conform formulei de mai jos:
![]()
(formula 2.13)
Valoarea acestui coeficient exprima un raport procentual dintre abaterea standard si medie. Cu cat este mai mare, cu atat media putem spune ca media este mai putin "reprezentativa" pentru distributia respectiva, data fiind ponderea ridicata a imprastierii. Utilizarea coeficientului de variatie este limitata la valorile masurate pe scale de raport, cu origine naturala 0. In cazul a doua variabile a caror origine este diferita una de alta, diferentele dintre valori (abaterea standard) raman aceleasi dar media se schimba, fapt care face ca raportul exprimat in formula sa fie modificat iar comparatia a doi coeficienti de variatie, irelevanta. In plus, pe o scala de interval cu valori negative se poate ajunge la medie egala cu 0, ceea ce face formula inaplicabila.
Utilitatea coeficientului de variatie vine de la faptul ca valoarea sa mai este legata de unitatea de masura. Diferenta dintre doua valori cv poate fi interpretata ca diferenta de imprastiere a celor doua variabile, chiar daca masoara lucruri diferite.
Sunt propuse anumite limite de interpretare a acestui indicator, astfel:
daca cv<15%, imprastierea este mica si, deci, media este reprezentativa
daca cv este cuprins intre 15%-30%, imprastierea este mijlocie si media este suficient de reprezentativa
daca cv este mai mare de 30%, imprastierea este mare si media are o reprezentativitate redusa
Calcularea coeficientului de variatie a unei distributii, inainte de integrarea ei in proceduri statistice inferentiale, este o metoda utila de verificare a masurii in care media, pe care se bazeaza de cele mai multe ori procedurile inferentiale, este legitima.
Alegerea indicatorului imprastierii
Abaterea standard este cea mai utilizata pentru scale de masurare interval/raport. Realizeaza cea mai buna combinatie intre calitatea estimarii si posibilitatea de a fundamenta inferente statistice.
Amplitudinea este un indicator nesigur si care nici nu poate fi calculat in cazul scalelor nominale
Pe distributii cu valori nedeterminate sau cu intervale deschise, se alege abaterea interquartila (semi-interquartila).
Expresia grafica a distributiilor poate fi descrisa sub doua aspecte esentiale: simetria si boltirea. O distributie este simetrica atunci cand valorile acesteia se impart in mod egal de o parte si de alta a valorilor tendintei centrale. Se numesc asimetrice (skewed) distributiile ale caror valori se concentreaza fie in zona valorilor mici (spre stanga) fie in zona valorilor mari (spre dreapta)
Distributie:simetrica asimetrica negativ asimetrica pozitiv
![]()
![]()
![]()
![]()
![]()
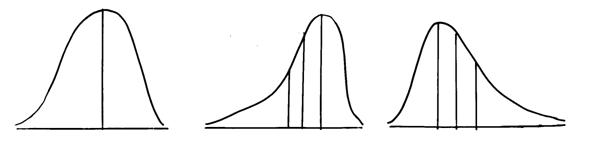
Medie Mediana Mod Mod
Mediana Medie
Mediana
Figurile de mai sus arata cum se plaseaza cei trei indicatori ai tendintei centrale in functie de simetria distributiei:
In cazul distributiilor (perfect) simetrice, Mo, Me si m se plaseaza pe aceeasi valoare
In cazul distributiilor asimetrice cei trei indicatori au pozitii diferite (vezi figura).
Mediana se plaseaza intotdeauna intre mod si medie. Din acest motiv, mediana este cea mai reprezentativa valoare pentru distributiile asimetrice
Media este afectata de valorile extreme, cu atat mai mult cu acestea sunt mai puternic deviate. Ca urmare, in cazul distributiilor puternic asimetrice, media nu este un indicator veridic al tendintei centrale.
Descrierea numerica a caracteristicii de simetrie/asimetrie se face cu ajutorul unui indicator statistic specific, numit indicator de "simetrie" sau de "oblicitate" (skewness, in limba engleza). Nu vom prezenta aici formula sa de calcul, destul de complicata, el urmand a fi obtinut usor cu ajutorul programelor specializate. Vom face insa cateva precizari cu privire la domeniul de variatie si semnificatia acestui indicator. Pentru o curba absolut simetrica, indicele de oblicitate (skewness) are valoarea 0 (zero), primind valori pozitive pentru curbele asimetric pozitive si valori negative pentru cele asimetric negative. Ca reper general de apreciere, recomandat de cei mai multi autori, un indice de oblicitate a carui valoare depaseste +1/-1 semnaleaza o asimetrie pronuntata a distributiei.
Caracteristica de boltire (kurtosis, in terminologia engleza) indica gradul de extindere pe verticala a curbelor de distributie. In termeni generali, sub aspectul boltirii, curbele pot fi de trei categorii:
Leptokurtice, cu majoritatea valorilor distribuite in zona mediei (au o forma "inalta" si "subtire")
Mezokurtice, cu o prezenta "moderata" a valorilor in zona mediei
Platikurtice, cu valori medii relativ putine si o forma aplatizata
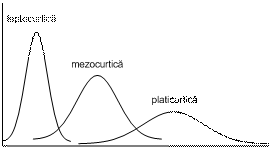
Desigur, o curba poate fi in acelasi timp si asimetrica si boltita excesiv, chiar daca imaginea de mai sus ilustreaza boltirea pe curbe simetrice.
Indicatorul numeric al boltirii (kurtosis) are o plaja de variatie in jurul valorii zero (care inseamna boltire medie, "normala", mezocurtica). Indicele de boltire pozitiva indica o curba "inalta" (leptocurtica), iar indicele de boltire negativa, o curba "aplatizata" (platicurtica). La fel ca si in cazul indicelui de oblicitate (skewness), cu cat acesta este mai indepartat de valorile +1/-1, avem de a face cu distributii cu abatere accentuata de la boltirea "normala".
Calcularea indicatorilor de simetrie si de boltire reprezinta modalitati importante de apreciere a caracteristicilor unei distributii. Acestia trebuie luati in considerare ori de cate ori utilizarea procedurilor statistice inferentiale reclama anumite caracteristici ale distributiilor.
Intrebari pregatitoare pentru evaluarea partiala 1
a) Pe ce scala de masurare se exprima culoarea ochilor?
b) Frecventa relativa cumulata se mai numeste si
c) Daca abaterea standard a unei distributii este 4, care este dispersia?
d) Pe ce scala se exprima atitudinea fata de statistica masurata pe o scala continua de la 1 (absolut antipatica) la 10 (absolut simpatica)?
e) Daca toate valorile unei distributii sunt marite cu aceeasi valoare, media distributiei
f) Daca toata valorile unei distributii sunt impartite la o valoare, abaterea standard a distributiei
Nota: Toate intrebarile vor cere raspunsuri scurte. Se va acorda maxim un minut pentru fiecare intrebare.
TEMA PENTRU ACASA
1. Tabelul de mai jos contine doua distributii de valori (variabile). Una reprezinta scorurile la un test de evaluare a timiditatii, cealalta la un test de evaluare a sentimentului de singuratate. Aflati pentru fiecare distributie in parte: modul, mediana, media
Timiditate
Singuratate
29
27
28
35
36
30
41
51
25
30
15
20
33
47
40
42
33
40
20
33
35
28
26
40
32
22
23
15
2. Ce indicator al tendintei centrale poate fi utilizat pentru a descrie fiecare dintre urmatoarele distributii ipotetice (motivati fiecare alegere):
a) Frecventa cardiaca pentru un grup de subiecti aflati inaintea unei sedinte de aerobic (masurata in batai pe minut)
b) Preferinta religioasa a unui esantion de participanti la o conferinta internationala
c) Evaluarea motivatiei pentru zbor a unui grup de candidati piloti, apreciata ca una dintre urmatoarele valori; (1) foarte slaba; (2) slaba; (3) medie; (4) buna; (5) foarte buna
d) Venitul anual al angajatilor unei societati (in lei)
e) Tipurile de fobii diagnosticate pentru un grup de pacienti
f) Timpul consumat cu rezolvarea unor probleme de tip cognitiv (masurat in secunde)
g) Inaltimea in centimetri a unui grup de baschetbalisti
3) Calculati amplitudinea, abaterea interquartila, abaterea medie, si abaterea standard, pentru urmatoarele doua distributii de valori:
a) 3,8,13,23,25,26, 26,27,28,28,29, 30,32,41,49,56
b) 17,19,22,23,25,26,26,27,28, 28,29,30,32,35,35,36
4) Care dintre cele doua distributii de mai sus are o imprastiere mai mare (motivati raspunsul)
5) Care dintre indicatorii imprastierii (amplitudine, abatere interquartila, abatere standard) ar trebui alesi pentru fiecare dintre urmatoarele situatii:
g) Distributia este puternic asimetrica, avand cateva valori extreme intr-o singura directie a curbei
h) Intentionati sa utilizati proceduri statistice avansate (de exemplu, sa emiteti aprecieri asupra "populatiei" pe baza datelor de esantion )
i) Vreti sa stiti intinderea maxima a unei distributii
j) Vreti ca fiecare valoare a distributiei sa fie luata in considerare
k) Valoarea cea mai mare a distributiei este "mai mult de 10"
[1][1] O prezentare extensiva a tipurilor de reprezentari grafice poate fi gasita in Statistica, Electronic Textbook, 1984-1999, StatSoft Inc., Graphical techniques
[2][1] In mod normal, reprezentarea boxplot se construieste independent de tabelul de frecvente. Daca le-am asociat in imaginea de mai sus, am facut-o doar cu scop didactic, pentru a pune mai clar in evidenta mecanismul de elaborare
[4][1] Vom vedea mai departe ca aceasta afirmatie nu este decat o ipoteza, pana la verificarea ei statistica.
[5][2] In continuare ne vom raporta la media de esantionare. Se subintelege ca, pentru cazul unei populatii, media va fi scrisa cu litera m (miu).
[6][3] Aceasta operatie este permisa de proprietatile mediei