
|
|
|
Constante fizice
Sarcina electronului e = q = 1.6 10-19 C
Permitivitatea spatiului liber eo = 8.86 10-14 F/cm
Tensiune termica (T = 300 K) ![]() k T = 0.0259 eV
k T = 0.0259 eV
Masa electronului liber in repaos mo = 9.11 10-31 Kg
Proprietati importante ale principalelor materiale semiconductoare
Constanta retelei [A]
5.43
5.65
5.65
Temperatura de topire [oC]
1415
937
1238
Constanta dielectrica - er
11.7
16.0
13.1
Largimea benzii interzise - EG [eV]
1.12
0.66
1.42
Concentratie intrinseca de
purtatori - ni [cm-3]
1.45 1010
2.4 1013
1.8 106
Mobilitatea electronilor - mn [cm2/V.s]
1350
3900
8500
Mobilitatea electronilor - mp [cm2/V.s]
480
1900
400
Nota Valorile sunt orientative, valabile pentru semiconductori in stare pura (nedopati). Mobilitatea scade puternic cu cresterea dopajului.
Relatii utile:
Conditia
de neutralitate: ![]()
Echilibru
termic: ![]()
Legea lui
Ohm: ![]()
![]()
Ecuatiile de transport: ![]()
![]()
Relatiile lui
Einstein: ![]()
![]()
Ecuatiile de
continuitate: ![]()
![]()
La nivel mic de injectie, vitezele nete de recombinare:
![]()
![]()
2.1. Un monocristal de material semiconductor cu concentratia intrinseca ni este dopat cu NA acceptori si ND donori pe cm3. Sa se calculeze concentratiile de purtatori mobili de sarcina, daca monocristalul se afla la echilibru termic, la temperatura camerei.
Rezolvare. Se presupune valabila ipoteza ionizarii complete a atomilor de impuritate. Se utilizeaza conditia de neutralitate a sarcinii electrice si conditia de echilibru termic:
![]()
![]()
Sistemul de doua ecuatii de mai sus are doua necunoscute. Presupunem un semiconductor de tip n (deci ND > NA). Rezulta:
![]()
![]()
Solutia generala a ecuatiei de gradul doi este:
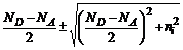
Semnul (+) corespunde purtatorilor majoritari si semnul (-) purtatorilor minoritari. Deci:
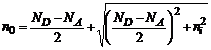
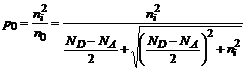
![]()
Cea de a doua relatie pentru p0 nu poate fi utilizata practic deoarece, in general, cele doua numere care se scad au valori foarte apropiate si eroarea cu care se obtine rezultatul este mare.
In majoritatea cazurilor practice se indeplineste conditia ND - NA >> ni si relatiile de mai sus devin:
![]()
![]()
In cazul unui semiconductor de tip p (deci ND < NA) se procedeaza similar. Daca NA - ND >> nI se obtine:
![]()
![]()
2.2. Un monocristal de siliciu de tip n se afla la echilibru termic si este dopat cu ND = 1016 cm-3 donori si NA = 0 cm-3 acceptori. Sa se calculeze concentratiile de electroni si goluri la T = 300 K.
Rezolvare. Se considera valabila ipoteza ionizarii complete. Deoarece ND >> ni = 1.45 1010 cm-3. Deci (problema 2.1):
n0 = 1016 cm-3 p0 = 2.1 104 cm-3
2.3. Un monocristal de germaniu de tip n se afla la echilibru termic si este dopat cu ND = 5.0 1013 cm-3 donori si NA = 0 cm-3 acceptori. Sa se calculeze concentratiile de electroni si goluri la T = 300 K.
Rezolvare. In cazul germaniului ni = 2.4 1013 cm-3, deci trebuiesc utilizate relatiile exacte de calcul deduse in problema 2.1. Rezulta:
n0 = 5.97 1013 cm-3 p0 = 9.66 1012 cm-3
2.4. Un monocristal de siliciu de tip n se afla la echilibru termic si este dopat cu ND = 1016 cm-3 donori si NA = 3 1015 cm-3 acceptori. Sa se calculeze concentratiile de electroni si goluri la T = 300 K.
Raspuns. n0 = ND - NA = 7 1015 >> ni. p0 = 3 10 4 cm-3 .
2.5. Sa se calculeze la temperatura camerei, in cazul semiconductorilor puri, rezistivitatea unui monocristal de: a) siliciu; b) germaniu c) GaAs.
Rezolvare. Se utilizeaza relatia:
![]()
unde n = p = ni. Rezulta:
a) s = 4.25 10-6 W-1 cm-1
b) s = 2.23 10-2 W-1 cm-1
c) s = 2.56 10-9 W-1 cm-1
Rezulta ca GaAs este practic un bun izolant (cu aplicatii in circuitele integrate) iar substratele de siliciu pur au o rezistivitate ridicata.
2.6. Sa se calculeze tipul impuritatilor si concentratia lor pentru a obtine la temperatura camerei un monocristal de siliciu cu rezistivitate maxima.
Rezolvare. Datorita diferentei dintre mobilitatile electronilor si golurilor, rezistivitatea maxima (deci conductivitatea minima) nu se obtine pentru semiconductorul intrinsec ci pentru un semiconductor de tip p usor dopat cu acceptori. La echilibru termic:
![]()
![]()
Rezulta urmatoarea functie de p0 pentru care trebuie gasit minimul prin derivare:
![]()
![]()
Solutia este:
![]()
![]()
Conductivitatea rezulta s = 4.26 10-6 W-1 cm-1 si rezistivitatea r = 2.35 105 W cm.
2.7. Un semiconductor din siliciu compensat de tip n are o conductivitate s = 16 (W cm)-1 si o concentratie de impuritati acceptoare de NA = 5 1015 cm-3. Considerand mobilitatea independenta de concentratia de impuritati, sa se calculeze concentratia de impuritati donoare la temperatura camerei.
Rezolvare. Semiconductorul este de tip n deci ND > NA iar datorita faptului ca conductivitatea este mult mai mare decat cea a semiconductorului intrinsec rezulta ND - NA >> ni. Deci, cu ipoteza ionizarii complete:
![]()
Rezulta: ND = 7.91 1016 cm-3.
2.8. Intr-o bara semiconductoare de tip p, concentratia de purtatori variaza liniar intre p(0) > p0 si p(W) = p0. Se considera: p(0) = 103 p0. Sa se calculeze expresia densitatii de curent de goluri de difuzie.
Raspuns.
a)
![]()
- largimea regiunii de sarcina spatiala: ![]()
![]()
![]()
- campul electric maxim: ![]()
- caracteristica statica: ![]()
- componenta de difuzie a curentului: 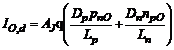
- componenta de generare-recombinare: 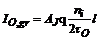
![]()
![]()
![]()
- coeficientul de multiplicare in avalansa: 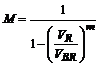
- rezistenta interna: ![]()
- capacitatea de difuzie: ![]()
- capacitatea de bariera: ![]()
Probleme rezolvate
2.9. Pentru o jonctiune pn abrupta cu NA = 1018 cm-3 si ND = 1016 cm-3, sa se calculeze inaltimea barierei interne de potential daca jonctiunea se afla la T = 300 K si este realizata din: a) siliciu; b) germaniu; c) GaAs.
Inaltimea barierei interne de potential se calculeaza cu relatia:
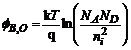
Cele trei materiale semiconductoare au valori diferite pentru concentratia intrinseca. Rezulta pentru:
- siliciu FBO = 0.819 V
- germaniu FBO = 0.433 V
- GaAs FBO = 1.287 V.
Se observa ca diferenta interna de potential este cu atat mai mare cu cat concentratia intrinseca este mai mica, deci largimea benzii interzise este mai mare.
O observatie utila pentru verificarea calculelor de acest tip este aceea ca inaltimea barierei interne de potential creste cu aproximativ 60 mV pentru fiecare ordin de marime al argumentului functiei logaritm.
2.10. O jonctiune abrupta din siliciu,
aflata la T = 300 K, are nivelele de dopaj NA = 1017
cm-3 si ND = 1015 cm-3.
Constantele de difuzie ale purtatorilor minoritati sunt Dn = 25 cm2/s
si Dp = 10 cm2/s. Timpul de viata al
purtatorilor de sarcina este ![]() .
.
a) Sa se calculeze concentratiile de purtatori in ipoteza ionizarii complete.
Trebuie remarcat ca intr-o jonctiune pn exista doua zone distincte, cu dopaje de impuritati diferite, deci trebuiesc calculate patru concentratii de purtatori. In zona n concentratiile sunt:
-
purtatori majoritari: ![]()
-
purtatori minoritari: ![]()
In zona n concentratiile sunt:
-
purtatori majoritari: ![]()
-
purtatori minoritari: ![]()
b) Sa se calculeza inaltimea barierei interne de potential.
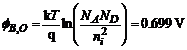
c) Sa se calculeze largimea regiunii de sarcina spatiala pentru echilibru termic si pentru polarizarea jonctiunii la VF = 0.5 V si VR = 10 V.
Deoarece NA >> ND (cazul jonctiunii abrupte asimetrice) largimea regiunii de sarcina spatiala este data de:
![]()
Rezulta:
- vD = 0 V l = lO = 9.52 10-5 cm = 0.952 mm
- vD = VF = 0.5 V l = 5.078 10-5 cm = 0.508 mm
- vD = VR = 10 V l =3.723 10-4 cm = 3.723 mm
Largimea regiunii golite este cu atat mai mare cu cat tensiunea inversa aplicata pe jonctiune este mai mare.
d) Sa se calculeze campul electric maxim pentru echilibru termic si pentru polarizarea jonctiunii la VF = 0.5 V si VR = 10 V.
Campul electric maxim se calculeaza cu:
![]()
Din relatiile:
![]()
![]()
rezulta pentru jonctiunea abrupta:
![]() si
si ![]()
Se observa ca regiunea de sarcina spatiala se extinde cu precadere in zona n, mai slab dopata. Cazul jonctiunii in care NA >> ND (jonctiune asimetrica) se mai noteaza si p+n.
Numeric rezulta:
- vD = 0 V EM = 1.47 104 V/cm
- vD = VF = 0.5 V EM = 7.84 103 V/cm
- vD = VR = -10 V EM = 5.746 104 V/cm
e) Sa se calculeze tensiunea de strapungere VB a jonctiunii stiind ca valoarea campului electric de strapungere este Ecr = 3 105 V/cm.
Valoarea campului critic la care apare strapungerea depinde atat de tipul semiconductorului, de forma geometrica a jonctiunii, de temperatura cat si de concentratiile de impuritati. Valoarea indicata in problema a fost obtinuta pe baza datelor experimentale pentru siliciu, in conditiile celorlalte date numerice ale problemei.
Rezulta:
![]()
Numeric: VB = 292 V.
f) Sa se calculeze componenta de difuzie a curentului prin dioda pentru polarizarea jonctiunii la VF = 0.5 V si VR = 10 V. Se presupune cazul jonctiunii "groase".
Componenta de difuzie a curentului prin dioda a fost calculata pentru jonctiunea pn ideala, la care, printre altele, se neglijau fenomenele de generare-recombinare din regiunea de sarcina spatiala. Densitatea curentului prin structura calculata in aceste conditii are expresia:
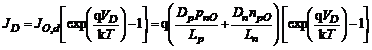
Aceasta expresie se poate rescrie inlocuind valorile densitatilor de purtatori minoritari la echilibru termic (calculate la punctul a) ca:
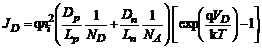
In expresia de mai sus singurele marimi necunoscute sunt lungimile de difuzie ale purtatorilor minoritari. Ele se calculeaza cu:
![]() = 3.54 10-3 cm = 35.4 mm
= 3.54 10-3 cm = 35.4 mm
![]() = 2.24 10-3 cm = 22.4 mm
= 2.24 10-3 cm = 22.4 mm
In cazul jonctiunii "groase" se presupune ca Ln si Lp sunt mult mai mici decat grosimea zonelor neutre situate de o parte si de alta a regiunii de sarcina spatiala.
Se obseva ca in cazul jonctiunii abrupte asimetrice (NA >> ND), expresia curentului poate fi scrisa:
![]()
Valoarea densitatii curentului de difuzie la saturatie este: JO,d = 1.5 10-10 A/cm2.
Rezulta deci: - vD = VF = 0.5 V JD = 8.44 10-2 A/cm2.
- vD = VR = -10 V JD = - JO,d = -1.5 10-10 A/cm2.
g) Sa se calculeze componenta de generare-recombinare a curentului prin dioda pentru polarizarea jonctiunii la VF = 0.5 V si VR = 10 V.
In cazul polarizarii in direct a jonctiunii pn, in regiunea de sarcina spatiala concentratia de purtatori mobili de sarcina creste mult peste valoarea de la echilibru termic. In aceasta zona apare fenomenul de recombinare a purtatorilor mobili de sarcina si prin jonctiune va trece o componenta a curentului neglijata la deducerea legii diodei ideale. In cazul polarizarii in invers a jonctiunii concentratiile de purtatori mobili de sarcina sunt sub valorile de la echilibru termic si apare fenomenul de generare a perechilor electron-gol. Si in acest caz apare o componenta suplimentara a curentului care se adauga celei de difuzie.
Expresia densitatii de curent datorata fenomenelor de generare-recombinare este:
![]()
Se remarca faptul ca dependenta curentului de tensiunea de polarizare are loc atat direct, prin intermediul functiei exponentiale, cat si indirect, prin intermediul largimii regiunii de sarcina spatiala l (deci trebuiesc utilizate rezultatele obtinute la punctul c).
Pentru VF = 0.5 V, rezulta: JD,rec = 1.77 10-3 A/cm2.
Comparand aceasta valoare cu cea obtinuta la punctul f pentru densitatea curentului de difuzie, rezulta ca, pentru siliciu, componenta de recombinare a curentului in direct prin jonctiune reprezinta o abatere importanta de la legea diodei ideale. Datorita dependentei reduse de tensiune prin intermediul largimii regiunii de sarcina spatiala, aceasta abatere va fi cu atat mai importanta cu cat tensiunea de polarizare in direct este mai mica. Aceasta abatere devine neimportanta la tensiuni de polarizare mai mari.
Pentru VR = 10 V, rezulta: JD,gen = - 8.64 10-7 A/cm2.
Comparand aceasta valoare cu cea obtinuta la punctul f pentru densitatea curentului de difuzie, rezulta ca componenta de generare a curentului invers este dominanta pentru jonctiunile din siliciu polarizate invers la temperatura camerei (este mai mare cu cateva ordine de marime).
h) Sa se calculeze rezistenta de semnal mic a jonctiunii polarizate in invers la VR = 10 V, daca aria jonctiunii este AJ = 10-2 cm2.
Calculul rezistentei interne de semnal mic (de fapt al conductantei) se face calculand panta caracteristicii statice I/V corespunzatoare punctului static de functionare dat. Tinand cont de punctele f si g, rezulta ca pentru polarizarea in invers a jonctiunii numai componenta de generare depinde de tensiunea aplicata (curentul de difuzie este practic constant la tensiuni inverse mai mari de 3kT/q).
Caracteristica curent de generare-tensiune devine in aceste conditii:
![]()
Prin derivare, conductanta de semnal mic se obtine ca:
![]()
Deci:
![]()
Dependenta de tensiune a largimii regiunii golite este (punctul c):
![]()
Dupa cateva calcule simple, rezulta:
![]()
Rezultatul final este:
![]()
Tinand cont de rezultatele obtinute la punctele b si g, rezulta rI = 2.48 MW. Rezultatul reprezinta o valoare foarte mare a rezistentei interne a unei jonctiuni polarizate invers, dar aceasta valoare este finita (nu infinita, dupa cum rezulta din legea diodei ideale).
i) Sa se calculeze componenta de difuzie a curentului prin dioda pentru VR = 10 V. Se cunoaste ca zona n are o largime Wn,O = 5 mm (distanta intre jonctiunea metalurgica si contactul ohmic).
Se calculeaza largimea efectiva Wn a zonei n neutre. Pentru aceasta se utilizeaza calculele facute la punctul c pentru l si observatia de la punctul d (regiunea de sarcina spatiala se extinde practic numai in zona n, mai slab dopata). Rezulta:
![]() =1.277 mm
=1.277 mm
Deoarece Lp = 22.4 mm >> Wn, rezulta ca formulele utilizat la punctul f nu mai pot fi utilizate in acest caz. Principala modificare care apare este cea a distributiei purtatorilor minoritari din zona n. Cu ipotezele simplificatoare in care a fost dedusa legea diodei ideale, ecuatia diferentiala pentru concentratia de purtatori minoritari in excess pn' din zona n neutra este:
![]()
Considerand originea x = 0 la jonctiunea metalurgica si sensul pozitiv al axei x spre zona n, conditiile la limita necesare pentru rezolvarea ecuatiei diferentiale se scriu ca:
![]() conditia
Schockley
conditia
Schockley
![]() la contactul
metalic nu sunt purtatori in exces.
la contactul
metalic nu sunt purtatori in exces.
Distributia purtatorilor minoritari in exces este:
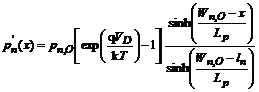
Daca Wn >> Ln se obtine distributia exponentiala de la jonctiunea "groasa". Daca Wn << Ln, atunci functia sinus hiperbolic poate fi aproximata:
Sinh (x) x, daca x 0. Rezulta o distributie liniara de x a purtatorilor minoritari in exces, data de:
![]()
Un caz asemanator va fi intalnit in cazul bazei tranzistorului bipolar. Curentul de difuzie al golurilor minoritare din regiunea n se calculeaza la marginea regiunii de sarcina spatiala x = ln rezultand:
![]()
Se observa ca acest rezultat poate fi obtinut din relatia curentului de difuzie de la punctul f (jonctiune "groasa") daca se inlocuieste lungimea de difuzie Ln cu largimea efectiva a regiunii n neutre Wn.
Aceasta ultima relatie este utila la lucrarea de laborator "Regimul static al jonctiunii pn", Tabelul 3. Jonctiunea pn a fost simulata in acel caz in absenta recombinarii purtatorilor de sarcina, deci pentru un timp de viata tO , deci pentru o valoare infinita a lungimii de difuzie a purtatorilor minoritari.
j) Sa se calculeze capacitatea de bariera a jonctiunii pentru VR = 10 V, daca aria jonctiunii este AJ = 10-2 cm2.
Capacitatea de bariera se calculeaza cu:
![]()
Tinand cont de rezultatul obtinut la punctul c (l = 3.723 10-4 cm) rezulta: Cb = 27.8 pF.
k) Sa se calculeze rezistenta serie a jonctiunii pentru VF = 0.5 V, daca aria jonctiunii este AJ = 10-2 cm2 iar grosimile zonelor p si n (de la jonctiunea metalurgica pana la contactele ohmice) sunt Wp,O = 100 mm si Wn,O = 250 mm. Estimati de la ce valoare a tensiunii in direct pe dioda efectul rezistentei serie devine semnificativ. Se considera T = 300 K.
Deoarece largimea regiunii de sarcina spatiala este mult mai mica decat grosimile zonelor n si p (punctul c), putem considera Wp Wp,O = 100 mm si Wn Wn,O = 250 mm. Regiunile neutre se comporta ca niste rezistoare a caror valoare poate fi calculata cu relatia:
![]()
Trebuiesc calculate rezistivitatile celor doua zone neutre. La nivel mic de injectie, rezulta:
![]() = 0.156 W.cm
= 0.156 W.cm ![]() = 6.25 W.cm
= 6.25 W.cm
Pentru calculul mobilitatilor purtatorilor au fost utilizate relatiile lui Einstein si a fost neglijata dependenta acestora de concentratia de impuritati. Pentru cele doua regiuni neutre rezulta urmatoarele valori ale rezistentelor serie care, la nivel mic de injectie, nu depind de tensiunea de polarizare a jonctiunii:
- zona p: Rp = 0.156 W - zona n: Rp = 15.62 W
Rezistenta serie a structurii rezulta: RS = 15.78 W
Pentru a estima efectul acestei rezistente asupra functionarii jonctiunii trebuie calculata caderea de tensiune pe rezistenta serie si comparata cu caderea de tensiune pe regiunea de bariera. Utilizand calculele de la punctele f si g pentru VF = 0.5 V, rezulta un curent prin dioda ID 0.844 mA, deci o cadere de tensiune pe rezistenta serie:
RS ID = 13.3 mV,
Valoarea obtinuta este neglijabila fata de caderea de tensiune pe jonctiune de 500 mV. Consideram ca efectul rezistentei serie devine semnificativ daca caderea de tensiune pe ea este de 10% din caderea de tensiune pe regiunea de bariera. Daca consideram ca prin structura trece numai curent de difuzie (vezi punctul g), tensiunea dorita se obtine din rezolvarea ecuatiei neliniare:
![]()
Cu IO,d = 3.75 10-12 A, rezulta VF = 0.536 V.
2.11. Sa se calculeze diferenta interna de potential, largimea regiunii de sarcina spatiala si campul electric maxim pentru o jonctiune pn abrupta din siliciu, aflata la echilibru termic, la T = 300 K, cu dopajele uniforme NA = 1018 cm-3 si a) ND = 1015 cm-3; b) ND = 1016 cm-3; c) ND = 1017 cm-3; d) ND = 1018 cm-3.
Sa se repete calculul pentru cazul germaniului.
2.12. Sa se calculeze diferenta interna de potential, largimea regiunii de sarcina spatiala si campul electric maxim pentru o jonctiune pn abrupta din GaAs, aflata la echilibru termic, la T = 300 K, cu dopajele uniforme NA = 1018 cm-3 si a) ND = 1015 cm-3; b) ND = 1016 cm-3; c) ND = 1017 cm-3; d) ND = 1018 cm-3.
2.13. Se da o jonctiune pn din GaAs abrupta, uniform dopata, la T = 300 K. La echilibru termic numai 20% din largimea regiunii de sarcina spatiala se afla in regiunea p. Bariera interna de potential este fBO = 1.2 V. Sa se determine: a) dopajele NA si ND; b) largimea regiunii de sarcina spatiala ln si lp; c) campul electric maxim.
Indicatie. Se pleaca de la conditia lp = 0.2 l. Rezulta NA = 4 ND. Dopajele se calculeaza apoi din valoarea lui fBO
2.14. O jonctiune abrupta din siliciu, aflata la T = 300 K, are nivelele de dopaj NA = 5 1015 cm-3 si ND = 1015 cm-3. Aria jonctiunii este AJ = 10-2 cm2 si jonctiunea este polarizata la o tensiune inversa VR = 5 V. Sa se calculeze: a) diferenta interna de potential; b) largimea regiunii de sarcina spatiala; c) campul electric maxim; d) capacitatea totala a jonctiunii.
2.15. Se considera o jonctiune pn uniform dopata din GaAs la
T = 300 K. Capacitatea jonctiunii la polarizare zero este Cj(0)
iar la o tensiune inversa de 10 V, capacitatea este Cj(10). Raportul
dintre aceste capacitati este ![]() . La tensiunea inversa de 10 V, largimea regiunii din
sarcina spatiala din zona p este de
4 ori mai mica decat largimea regiunii de sarcina spatiala din regiunea n. Sa se calculeze diferenta interna de
potential si dopajele din regiunile n
si p.
. La tensiunea inversa de 10 V, largimea regiunii din
sarcina spatiala din zona p este de
4 ori mai mica decat largimea regiunii de sarcina spatiala din regiunea n. Sa se calculeze diferenta interna de
potential si dopajele din regiunile n
si p.
Indicatie. Deoarece 4 lp = ln
rezulta NA = 4 ND. Pentru tensiuni de polarizare mai mici
sau egale cu zero, capacitatea jonctiunii este capacitate de bariera, care este
invers proportionala cu largimea regiunii de sarcina spatiala. Rezulta: ![]() , deci FBO = 0.9 V si ND = 2.38 1017
cm-3.
, deci FBO = 0.9 V si ND = 2.38 1017
cm-3.
2.16. O jonctiune abrupta din siliciu,
aflata la T = 300 K, are nivelele de dopaj NA = 5 1015
cm-3 si ND = 1015 cm-3.
Constantele de difuzie ale purtatorilor minoritati sunt Dn = 25 cm2/s
si Dp = 10 cm2/s. Timpul de viata al
purtatorilor de sarcina este ![]() . Jonctiunea este polarizata la o tensiune directa VF =
0.6 V. Sa se calculeze:
. Jonctiunea este polarizata la o tensiune directa VF =
0.6 V. Sa se calculeze:
a) componenta de difuzie a curentului prin jonctiune;
b) componenta de generare-recombinare a curentului;
c) la ce tensiune componenta de difuzie a curentului egaleaza componenta de generare-recombinare;
d) sa se determine campul electric din regiunea p neutra.
2.17. O jonctiune abrupta din GaAs,
aflata la T = 300 K, are nivelele de dopaj NA = 5 1015
cm-3 si ND = 1015 cm-3.
Constantele de difuzie ale purtatorilor minoritati sunt Dn = 150 cm2/s
si Dp = 7.5 cm2/s. Timpul de viata al
purtatorilor de sarcina este ![]() . Jonctiunea este polarizata la o tensiune inversa VR =
10 V. Sa se calculeze:
. Jonctiunea este polarizata la o tensiune inversa VR =
10 V. Sa se calculeze:
a) componenta de difuzie a curentului prin jonctiune;
b) componenta de generare-recombinare a curentului.
2.18. O jonctiune abrupta din germaniu,
aflata la T = 300 K, are nivelele de dopaj NA = 5 1015
cm-3 si ND = 5 1014 cm-3.
Mobilitatile purtatorilor sunt mn = 3800 cm2/(V.s)
si mp = 1800 cm2/(V.s).
Timpul de viata al purtatorilor de sarcina este ![]() . Jonctiunea este polarizata la o tensiune inversa VR =
10 V. Sa se calculeze:
. Jonctiunea este polarizata la o tensiune inversa VR =
10 V. Sa se calculeze:
a) componenta de difuzie a curentului prin jonctiune;
b) componenta de generare-recombinare a curentului.
2.19. O jonctiune abrupta din germaniu,
aflata la T = 300 K, are nivelele de dopaj NA = 5 1015
cm-3 si ND = 5 1014 cm-3.
Mobilitatile purtatorilor sunt mn = 3800 cm2/(V.s)
si mp = 1800 cm2/(V.s).
Timpul de viata al purtatorilor de sarcina este ![]() . Jonctiunea este polarizata la o tensiune directa VF =
0.15 V. Sa se calculeze:
. Jonctiunea este polarizata la o tensiune directa VF =
0.15 V. Sa se calculeze:
a) componenta de difuzie a curentului prin jonctiune;
b) componenta de generare-recombinare a curentului.
2.20. O jonctiune abrupta pn din siliciu are urmatorii parametrii:
- grosimea zonei n: Wn,O = 2 mm;
- grosimea zonei p: Wp,O = 200 mm;
- constantele de difuzie: Dn = 25 cm2/s si Dp = 10 cm2/s;
- rezistivitatea zonei n: rn = 0.5 W.cm;
- rezistivitatea zonei p: rp = 0.04 W.cm;
- timpul de viata al purtatorilor: ![]() ;
;
- aria jonctiunii: AJ = 10-4 cm2;
Sa se calculeze:
a) curentul prin structura la VR = 10 V;
b) curentul prin structura la VF = 0.6 V;
c) rezistenta serie a structurii la echilibru termic;
d) capacitatea structurii la echilibru termic si trasati dependenta capacitatii de bariera de tensiunea inversa pe jonctiune.
2.21. Se da o jonctiune pn din GaAs polarizata invers la o tensiune VR = 5 V. Se cunosc parametrii: NA = ND = 1016 cm-3; Dn = 200 cm2/s; Dp = 6 cm2/s;
tn tp tO = 10-8 s; T = 300 K. Sa se calculeze densitatea curentului de difuzie si densitatea curentului de generare. Sa se compare valorile obtinute cu cele corespunzatoare cazului in care jonctiunea este relizata din siliciu.
2.22. O jonctiune abrupta asimetrica p+n din siliciu, uniform dopata, este proiectata pentru o tensiune minima de strapungere de VB = 15 V. Sa se determine concentratia maxima de impuritati a zonei mai slab dopate. Se considera campul electric critic egal cu 4 105 V/cm.