|
|
|
Diferite enunturi ale principiului al treilea al termodinamicii
Conform ecuatiei (XV.3) la T = 0 K, capacitatile
calorice ale reactantilor si produsilor sunt identice. Aplicarea
teoriei cuantice la interpretarea caldurii specifice a solidelor
arata ca Cp
pentru solide tinde catre zero la zero absolut si deci, 
este zero sau finit.
Ecuatia (XV.3) se poate scrie:
(XV.4)
Conform ecuatiei (XV.2), in stare solida, la zero absolut, toate substantele au o valoare identica a entropiei. Entropia substantei solide la temperatura T este deci:
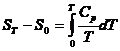(fara transformari polimorfe)
si deoarece este finit sau zero la
0 K, rezulta ST - S0 ≥ 0, cu alte cuvinte
valoarea minima posibila a entropiei unei substante corespunde
temperaturii de 0 K.
Planck completeaza teorema lui Nernst, enuntand principiul al treilea sub forma: entropia unui cristal perfect pur, la zero absolut, este zero (corect: valoarea coventionala a entropiei este zero):
S(T = 0) = S0 = 0 (XV.5)
Ecuatia (XV.5) verifica si ecuatia: (DS)T = 0 = 0.
Principiul al treilea include astfel si teorema lui Nernst, dar are avantajul unor aplicatii exacte.
Prin cristal perfect se intelege aranjarea particulelor in retea, fara nici o modificare. In termeni mai generali, relatia (XV.5) se aplica sistemelor la echilibru intern termodinamic (sisteme complet determinate prin valoarea presiunii, temperaturii si prin numarul de particule) in raport cu toti factorii. De exemplu, un cristal poate fi in echilibru termodinamic intern in raport cu vibratiile termice si cu simetria cristalina, dar nu si in raport cu distributia izotopilor in retea.
Principiul al treilea se poate enunta, deci, sub forma: contributia la entropia sistemului, datorita fiecarui factor in raport cu care sistemul este in echilibru termodinamic intern, se anuleaza la 0 K.
Conditia de echilibru termodinamic intern nu este o restrictie speciala a principiului al treilea. Aceasta conditie trebuie sa fie indeplinita de sistem pentru definirea tuturor marimilor termodinamice.
Exemplul 3 Sa se arate ca, in conformitate cu principiul al treilea, coeficientii de dilatatie si de presiune se anuleaza la 0 K.
Rezolvare:
Entropia unui cristal la temperatura T, fara transformari de faza in intervalul 0 - T, este:
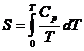
de unde, prin derivare, se obtine:
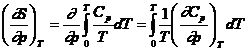
Dar, conform ecuatiei (XIV.41):
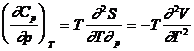
si deci:
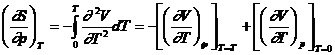
Rezulta, potrivit ecuatiei (XIV.41), c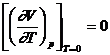a:
(a)
Experimental, s-a dovedit aceasta in cazul cuprului, aluminiului, argintului, diamantului, clorurii de sodiu, bioxidului de siliciu, fluorurii de calciu si piritei (pana la -250 oC).
Din ecuatia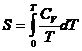 
, prin derivare in raport cu volumul, se obtine:
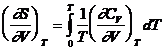
si, asemanator cazului examinat inainte:
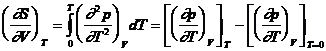
de unde:
, la T = 0 K (b)
Acelasi rezultat (b) se poate obtine direct din (a) utilizand ecuatia (V.3) si observand faptul ca coeficientul de compresibilitate al solidelor nu se modifica mult cu temperatura si are o valoare finita la 0 K.
Acest rezultat se poate generaliza pentru un sistem definit, la temperatura T, de coordonatele generalizate x1, x2 cu fortele corespunzatoare X1, X2
Potrivit teoremei lui Nernst:
; 
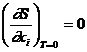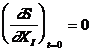
si prin relatia de tip Maxwell (XIV.38-41) se obtine:
si la T = 0
Ecuatiile obtinute se aplica pentru urmatoarele marimi: tensiunea superficiala, forta electromotoare a unui element galvanic, susceptibilitatea magnetica.
