Modele pentru jonctiunea pn

1. Introducere

Pentru studierea jonctiunii pn au fost dezvoltate doua modele : analitic si numeric.

Modelul analitic al jonctiunii pn se bazeaza pe urmatoarele ipoteze principale:

• Existenta in jurul jonctiunii a unei zone de sarcina spatiala, iar in afara acesteia a unor zone quasineutre
• Caderea de tensiune pe zonele neutre este neglijabila
• In zonele neutre purtatorii minoritari se deplaseaza predominant prin difuzie
• La marginile zonei de sarcina spatiala valorile pentru concetratiile de purtatori sunt cele date de conditiile lui Shockley

Modelul numeric al jonctiunii  pn se bazeaza pe rezolvarea numerica a sistemului de ecuatii al semiconductorilor. Nici una din ipotezele de mai sus nu mai este necesara. Avantajele modelului numeric sunt:

• Precizia rezultatelor este mult mai ridicata putandu-se face, in ipoteza utilizarii unor modele corecte pentru mobilitate si  recombinare, o descriere cantitativa a functionarii jonctiunii pn care chiar in cazul unor situatii dificil de tratat analitic cum ar fi cazul nivelului mare de injectie
• Permite utilizarea unor modele pentru mobilitate si recombinare mult mai apropiate de realitatea fizica

Lucrarea isi propune compararea rezultatelor obtinute folosind cele doua modele.

2.Modele pentru jonctiunea pn.

2.1 Modelul analitic.

Latimile zonelor de sarcina spatiala pot fi obtinute folosind relatiile:

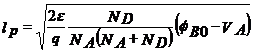
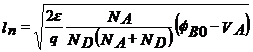
Diferenta de potential este data de relatia:

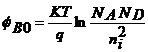
Campul electric maxim poate fi calculat folosind formula:

Conditiile Shockley la limita sarcinii spatiale:

2.2 Modelul numeric.

Ecuatiile folosite sunt:

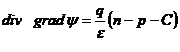
Setul de ecuatii care trebuie rezolvat numeric este:

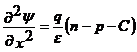Pentru o analiza unidimensionala:

Conditiile la limita folosite sunt:

np - n_i² = 0 

n - p - C = 0

Modelarea parametrilor fizici.

Mobilitatea

Mobilitatea purtatorilor intr-un semiconductor este legata de fenomenele de ciocnire si imprastiere pe care le sufera acestia. Simulatorul ofera doua posibilitati de modelare a mobilitatii: mobilitati constante si mobilitati dependente de concentratia impuritatilor de dopare si de intensitatea campului electric. Pentru cazul mobilitatii constante se utilizeaza urmatoarele valori:

_n = 1330 cm²/Vs

_p = 495 cm²/Vs

Fenomenul de saturatie a vitezei de drift in campuri electrostaticeintense a fost inclus in simulator folosind urmatorul model:

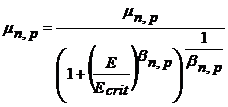
Recombinarea.

Recombinarea se poate neglija (R = 0) sau se poate utiliza modelul Shockley - Read -  Hall:

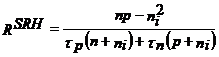
Desfasurarea lucrarii.

1.Pentru un dispozitiv cu N_A = 10¹⁸ cm^-3 si N_D =  10¹⁷ cm^-3 se determina distributia densitatii de sarcina a campului electric si potentialul electrostatic pentru V_A = 0V, -4V, -8V, -12V.

Rezultatele au fost trecute in tabelul urmator:

Graficele ln(V), lp(V) si E_max(V) sunt date in continuare:

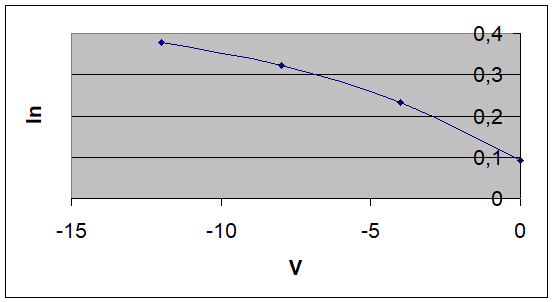
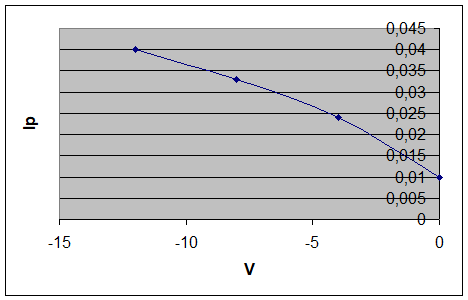
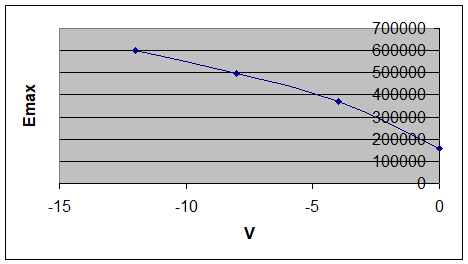
2. Se analizeaza in continuare indeplinirea ipotezelor Shockley la marginile zonelor de sarcina aplicata in cazul unei recombinari nule in functie de tensiunea directa aplicata.

Pentru aceasta se vor determina concentratiile de electroni si goluri pentru o structura la V_a=0.7, 0.8, 0.9, 1.0, 1.1V.

Rezultatele au fost trecute in tabelul urmator:

Graficul sunt urmatoarele:

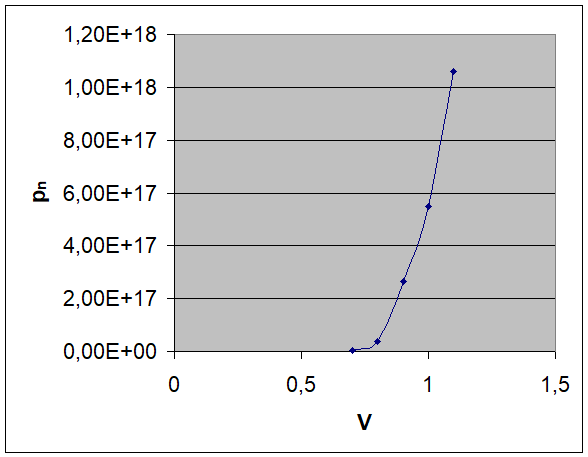
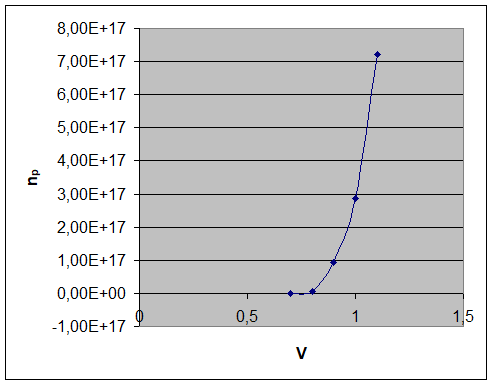
Caracteristica statica este data de urmatorul tabel: