Legea fluxului magnetic

Modelele acestei legi au doua forme de exprimare: una globala, relativa la orice suprafata inchisa dintr-un camp electromagnetic si alta locala relativa la orice punct P din camp.

Forma globala a legii fluxului magnetic

Sub aceasta forma, legea fluxului magnetic (adica fluxul vectorului inductie magnetica ) se refera la orice suprafata inchisa dintr-un camp magnetic prin care intotdeauna fluxul magnetic este egal cu zero, ceea ce se reprezinta prin modelul:

, (1.67)

sau -exprimandu-se fluxul magnetic prin definitia sa ( 1.36 )- prin modelul:

, (1.67')

in care sensul elementului de arie orientat, este ales conventional spre exteriorul suprafetei inchise , pe directia normalei locale.

Legea (1.67) este general valabila, fara restrictii.

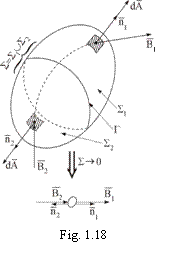
Legea (1.67') arata ca liniile de camp magnetic, adica axele unor tuburi de flux magnetic unitar ( de 1Wb ) sunt linii inchise. Intr-adevar, considerandu-se pe o suprafata inchisa din campul un contur inchis (fig. 1.18 ), care separa suprafata in doua suprafete si cu , astfel ca , legea (1.67') va deveni:

,

de unde rezulta:

sau , (1.68)

care arata ca, la acelasi sens al orientari lui , oricare ar fi ea pe sau (spre exteriorul suprafetei ): caci (v. fig. 1.18 ) si -la limita cand , care poate fi oricare, tinde catre zero ()- rezulta ca , ceea ce indica continuitatea liniilor de camp, fara puncte de convergenta sau divergenta (v. fig. 1.18), fapt exprimat -mai evident- de forma locala a fluxului magnetic.

Egalitatea (1.68) arata si faptul ca fluxul magnetic prin orice suprafata deschisa ce se sprijina pe acelasi contur are aceeasi valoare absoluta, adica .

Legea (1.67) mai arata ca, daca , in interiorul suprafetei nu mai exista elemente care sa modifice fluxul magnetic, deci nu exista ,,sarcini" (,,mase") magnetice separate (de un anumit semn, de exemplu numai Nord sau numai Sud, separate - v. Fizica).

Forma locala a legii fluxului magnetic

Aplicandu-se formula lui Gauss-Ostrogradski (v. § 9.1.2) legii (1.67'), rezulta:

,

si, deoarece si volumul inchis de aceasta suprafata sunt oricare din camp, iar , mai reiese ca in orice punct din campul :

(1.69)                ,

sau (mai simplu scris):

(1.69')                            ,

care constituie modelul general al formei locale a legii fluxului magnetic. Ea arata ca, in orice situatie, campul de inductie magnetica (si mai general, campul magnetic) este un camp de divergenta nula, care nu are puncte de izvor sau puncte de puturi magnetice.

Inductia magnetica pe suprafetele de discontinuitate

Daca o suprafata deschisa separa un domeniu in doua domenii omogene, in care inductia magnetica are valorile diferite si atunci in orice punct P al lui S_d, la trecerea dintr-un mediu in celalalt, componentele normale la ale lui si sunt egale, adica:

(1.70)                   ,

ceea ce inseamna ca pe suprafetele de discontinuitate ale inductiei magnetice componentele sale normale se conserva.

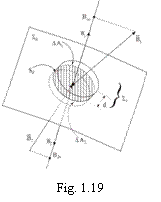Aceasta situatie rezulta din legea fluxului magnetic (1.67') scrisa pentru o suprafata inchisa foarte mica in forma de disc cilindric, cu fetele frontale si (fig. 1.19) situate de o parte si de alta a suprafetei de discontinuitate in imediata ei apropiere, paralele la si cu suprafata laterala normala pe inchizand punctul considerat. ,,Grosimea" discului este extrem de mica: << , unde , astfel ca idealizat fetele discului si sunt ,, lipite " de de-o parte si de alta a sa.

Aplicarea legii (1.67') suprafetei inchise duce la:

sau, deoarece la limita (daca , si ) , rezulta:

.

Pentru ca in conformitate cu conventia de semn a normalei la din legea (1.67'), , iar (adica componenta lui dupa directia normalei la in punctul P , deci componenta normala a inductiei ), ultima egalitate devine:

sau ,

care este egalitatea (1.70) de conservare a componentelor normale ale inductiei magnetice pe suprafetele de discontinuitate.