|
|
|
FUNCTII SI POTENTIALE TERMODINAMICE
Am stabilit anterior ca un sistem termodinamic in echilibru poate fi descris la scara macroscopica de un numar finit de variabile de stare. Conform principiului al doilea, entropia sistemului depinde de n variabile de stare extensive, U si Xi cu i=1, n-1. Pentru o evolutie infinitezimala a sistemului intre doua stari de echilibru, se poate scrie:
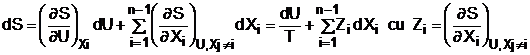
Cum
S si Xi sunt marimi extensive, parametri Zi se
numesc variabile entropice conjugate marimilor 
si sunt
marimi intensive. In aceasta reprezentare, inversul temperaturii
termodinamice T este parametrul entropic conjugat al energiei interne U:
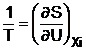
O
alta reprezentare, numita energetica este fondata pe
relatia: 
in care energia
interna este considerata ca o functie de parametrii extensivi S
si . Si in acest caz, pentru o evolutie a sistemului
intre doua stari de echilibru, se poate scrie:
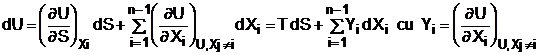
Cum
U si Xi sunt marimi extensive, parametrii Yi,
numiti variabile energetice conjugate pentru , sunt marimi intensive.
Parametrii Zi si Yi nu sunt independenti, deoarece:
si deci: 
(1.23)
1. Functii termodinamice
1.1. Energia interna
Functiile
termodinamice sunt functii energetice asociate unor ansambluri
determinate de variabile. Cea mai simpla functie termodinamica
este energia interna, functie de variabilele extensive S si : , cu variabile extensive
altele decat U.
Atunci
cand starea sistemului este caracterizata de doua variabile, de
exemplu S si V, sistemul este numit divariant. In cazul prezent 
si
diferentiala lui U este:
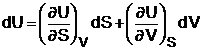
Dar 
(1.24)
De unde rezulta
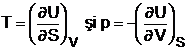
In plus, folosind relatia (1.23):
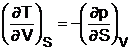
relatie numita relatia Maxwell relativa la energia interna.
Folosirea functiei U ca functie caracteristica este incomoda, deoarece este necesara cunoasterea dependentei energiei interne de entropie care nu este direct accesibila experientei. Din aceste considerente se prefera utilizarea altor functii termodinamice.
1.2. Transformarea Legendre pentru sisteme divariante
Vom
numi transformare Legendre, o transformare ce permite schimbarea
ansamblului de variabile, si deci de functii termodinamice, prin
scaderea din energia interna a produselor dintre variabila
extensiva X si variabila intensiva energetica asociata
Y. Intr-adevar, noua functie -XY conduce diferentiind la:
(1.25)
si procedand la fel pentru variabila S
se obtine: -XY-TS, de unde:
(1.26)
1.3. Entalpia
Vom numi entalpia unui fluid omogen, functia H de variabilele S si p definita prin transformarea Legendre a lui U in raport cu p:
(1.27)
Se deduce diferentiala lui H:
Rezulta 
de unde, prin diferentiere, se obtin
urmatoarele relatii:
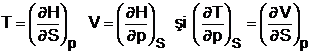(1.28)
ultima din relatiile de mai sus purtand numele de relatia Maxwell relativa la entalpie.
Energia libera
Vom numi energie libera sau functia lui Helmholtz, functia de stare F definita prin transformarea Legendre a lui U in raport cu T:
F= U [T]= U -T S (1.29)
Pentru un corp omogen diferentiala lui F este:
Rezulta 
din care, prin diferentiere, se obtin
relatiile:
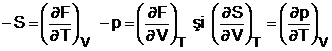(1.30)
Ultima din relatiile (1.30) este relatia lui Maxwell relative la energia libera.
1.5. Entalpia libera
Vom numi entalpie libera G, sau functia lui Gibbs, functia de stare definita prin transformarea Legendre a lui U in raport cu T si p:
(1.31)
sau
Pentru un corp omogen, diferentiala lui G se scrie:
Rezulta 
de unde, prin diferentiere, se obtin relatiile:
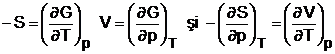(1.32)
Ultima din relatiile (1.32) este relatia Maxwell relativa la entalpia libera.
1.6. Relatiile lui Gibbs - Helmholtz
Aceste
relatii permit exprimarea functiilor U si H in functie de F
si G. Inlocuind in relatia F= U -T S, entropia prin valoarea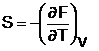 
se obtine:
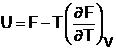(1.33)
Similar,
introducand in relatia G = H - T S expresia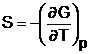 
se obtine:
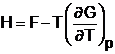(1.34)
Relatiile (1.33) si (1.34) sunt numite relatiile lui Helmholtz.
2. Potentiale termodinamice
Principiul
al doilea al termodinamicii ne-a permis sa stabilim sensul de
evolutie al sistemului, acesta fiind dat de inegalitatea 
. Dar entropia produsa nu este o functie de stare,
de aceea se cauta functii termodinamice care, in anumite
conditii pot, prin valorile lor in doua stari diferite, sa
dea sensul de evolutie al sistemului termodinamic. Aceste functii se
numesc potentiale termodinamice.
2.1. Evolutia si echilibrul termodinamic pentru un sistem izolat
Pentru un sistem izolat, bilantul entropic intre doua momente succesive t si t+ d t se scrie:
(1.35)
In consecinta, evolutia sistemului izolat este caracterizata de catre functia de stare S. Conditia de echilibru este:
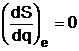
unde q poate fi oricare din parametri ce caracterizeaza starea sistemului termodinamic. Echilibrul este stabil daca
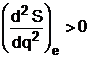
2.2. Evolutia si echilibrul unui sistem la volum si entropie constante
Din bilantul energetic si entropic pentru sistem intre momentele t si t + d t:
se poate deduce:
Cum la entropie si volum constante dS=0 si dV =0, de unde W=0, se obtine :
In concluzie, pentru un sistem real ce evolueaza la volum si entropie constante, conditia de evolutie este :
(1.36)
Conditia de echilibru este dU=0 deoarece atunci Sprod=0.
2.3. Evolutia si echilibrul unui sistem la presiune si entropie constante
Scriind bilantul energetic si entropic pentru un sistem intre momentele t si t+ d t:
se obtine
Deci evolutia reala la presiune si entropie constante se caracterizeaza prin scaderea entalpiei:
(1.37)
Egalitatea d H=0 corespunde echilibrului deoarece in aceste conditii Sprod=0.
2.4. Evolutia si echilibrul unui sistem la temperatura si volum constante
Scriind bilantul energetic si entropic pentru un sistem intre momentele t si t+ d t:
se obtine
Deci evolutia reala la temperatura si volum constante se caracterizeaza prin scaderea energiei libere:
(1.38)
Egalitatea d F=0 corespunde echilibrului deoarece in aceste conditii Sprod=0.
2.4. Evolutia si echilibrul unui sistem la temperatura si presiune constante
Scriind bilantul energetic si entropic pentru un sistem intre momentele t si t+ d t:
se obtine
deci evolutia reala la temperatura si presiune constante se caracterizeaza prin scaderea entalpiei libere:
(1.39)
Egalitatea d G=0 corespunde echilibrului.
Din cele demonstrate in acest paragraf se poate trage concluzia ca transformatele Legendre ale energiei sunt potentiale termodinamice. Mentionam ca se pot efectua transformari Legendre ale antropiei. Aceste transformari se numesc functii Massieu si au un rol important in fizica statistica.
