Etalonarea materialelor fotoelastice

Etalonarea materialelor fotoelastice

Diferenta tensiunilor principale σ₁ - σ₂, intr-un punct de pe suprafata modelului se determina cu expresia (38).

σ₁ - σ₂ = N.f_σ,

Daca se cunoaste ordinul de banda N in punctul respectiv si constanta fotoelastica de tensiune optica f_σ a modelului. Daca punctul se afla pe o izocromata, ordinul de banda este un numar intreg si corespunde ordinului izocromatei, iar daca se afla intre doua izocromate este fractionar si se determina cu una din metodele de compensare.

Constanta fotoelastica de tensiune a modelului este data de expresia (39)

,

si depinede de lungimea de unda a luminii folosite, de grosimea modelului si de proprietatile de birefrigenta ale materialului modelului.

Pentru un model fotoelastic cu grosimea h, care este analizat in lumina monocromatica cu lungimea de unda λ, constanta fotoelastica de tensiune a modelului se determina experimental, printr-o operatie de etalonare.

In practica se folosesc diferite procedee de etalonare, dintre care cele mai folosite sunt: etalonarea cu epruveta de tarctiune, etalonarea cu epruveta de incovoiere si etaloanarea cu disc comprimat diametral.

1 Etalonarea cu epruveta solicitata la tractiune

Epruveta folosita pentru etalonare se prelucreaza din acelasi material cu modelul si are forma unei barete prevazuta cu un concentrator in care se stocheaza izocromatele formate prin solicitarea baretei la tractiune cu sarcini aplicate progresiv (fig. 21,a).

Fig. 21 Epruveta solicitata la tractiune

In vederea determinarii constantei fotoelastice a modelului, se incarca epruveta mai intai cu o sarcina F₁, astfel incat franja de ordinul unu sa ajunga la conturul concentratorului. Intre timp se pot forma si franjele de ordinul doi si chiar trei. Franja ajunsa la contur, potrivit (38) este caracterizata de expresia σ₁ - σ₂ = N.f_σ, conturul fiind neincarcat, σ_2c = 0 si expresia devine

σ_1c = N₁.f_σ, (a)

Pe de alta parte tensiunile produse de sarcina F₁ in sectiunea epruvetei sunt:

(b)

Din (a) si (b) rezulta expresia pentru calculul constantei fotoelastice de tensiune a modelului

(c)

Daca sarcina aplicata epruvetei este crescuta treptat, astfel incat izocromatele de ordinele doi, trei etc, sa fie tangente la conturul concentratorului, folosind expresia (c) se determina valoarea constantei fotoelastice corespunzatoare fiecarei trepte de incarcare. Calculand, media acestor valori se obtine constanta fotoelastica de tensiune a modelului f_σ, cu perechile de valori F_i, N_i, deteminate experimental se poate trasa si curba de etalonare(fig. 21b).

2 Etalonarea cu epruveta solicitata la incovoiere

Din acelasi material cu modelul se confectioneaza o bareta de forma speciala, care este solicitata la incovoiere pura cu ajutorul unui dispozitiv cu parghii (fig. 22,a). Bareta solicitata progresiv este examinata intr-un polariscop cu lumina polarizata circular. Izocromatele care se formeaza de la contur sedeplaseaza catre axa barei, pe masura ce incarcarea creste (fig. 22,b).

O izocromata de un anumit ordin N, tangenta la contur, este caracterizata de expresia:

σ_1c - σ_2c = N.f_σ.

Conturul fiind neincarcat, σ_1c = 0 (fig. 22,c), si

σ_1c = N.f_σ, (d)

Tinand seama de notatiile din figura 22,a, tensiunea maxima pe conturul baretei poate fi calculata cu expresia

(e)

Din expresiile (d) si (e) se obtine relatia pentru calculul constantei fotoelastice

. (f)

Fig. 22 Epruveta solicitata la incovoiere

Cu aceasta expresie se calculeaza valorile constantei fotoelastice de tensiune a materialului corespunzatoare fiecarei izocromate, cu care apoi se determina valoarea medie a aceseia. Folosind perechile de valori F, N si in acest caz se poate trasa curba de etalonare.

3 Etalonarea cu disc comprimat diametral

Discul confectionat din acelasi material cu modelul fotoelastic este solicitat progresiv la compresiune pe directia diametrului vertical (fig. 23,a). Pentru acest caz particular de incarcare, tensiunile principale pe un element de suprafata in centrul discului se calculeaza cu expresiile:

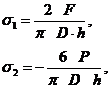(g)

unde F este forta aplicata, iar D si h sunt diametrul, respectiv grosimea discului.

Fig. 23 Disc comprimat diametral

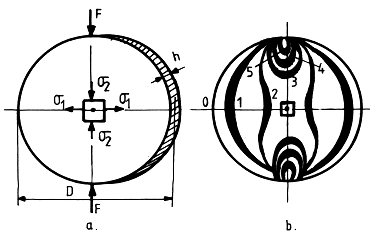
Diferenta tensiunilor principale in centrul discului va fi:

(h)

Discul astfel solicitat este introdus intr-un polariscop cu lumina polarizata circular si pentru fiecare treapta de incarcare se determina valoarea ordinului de banda N, folosind una din tehnicile de compensare prezentate mai sus.

Diferenta tensiunilor principale in centrul discului, pentru o anumita treapta de incarcare(fig. 23b) este:

σ₁ - σ_­2 = N.f_σ. (i)

Egaland relatiile (h) si (i) se obtine expresia pentru calculul constantei fotoelastice de tensiune a modelului:

. (j)

Constanta fotoelastica de tensiune a modelului determinata cu pocedeele prezentate mai sus reprezinta variatia tensiunilor tangentiale maxime din model (t_max = (σ₁ - σ₂)/2), necesare pentru a produce o variatie a ordinului de banda cu o unitate si se exprima in MPa/franja.

Pentru a caracteriza sensibilitatea unui material fotoelastic in raport cu altul, se defineste constanta fotoelastica de tensiune a materialului, prin expresia:

(45)

Aceasta constanta reprezinta variatia necesara a tensiunii tangentiale maxime, pentru a modifica ordinul de banda cu o unitate, intr-un model fotoelastic cu grosimea unitara si se exprima in N/mm.fr.

Considerand o relatie liniara intre tensiuni si deformatii, legea fotoelasticitatii conduce in final la o relatie similara cu (38)

, (46)

unde

, (47)

este constanta fotoelastica de deformatie optica a modelului si se exprima in μm/m.franja.

Constanta fotoelastica de deformatie a modelului reprezinta variatia necesara a lunecarii specifice maxime (g_max/2=ε₁ - ε₂), pentru a produce o modificare a ordinului de banda cu o unitate si se exprima in μm/m.franja. Si in acest caz se poate defini o constanta fotoelastica de deformatie a materialului

, (48)

care se exprima in μm/franja si reprezinta variatia lunecarii specifice maxime (g_max), care produce modificarea ordinului de banda cu o unitate, intr-un model cu grosimea unitate.

Intre coeficientii relativi de tensiune si deformatie optica ai materialul exista relatia:

, (49)

unde n si E sunt coeficientul lui Poisson, respectiv modulul de elasticitate longitudinal(constantele elastice) ale materialului fotoelastic.

Iar intre constantele fotoelastice de tensiune si deformatie ale modelului va rezulta urmatoarea relatie:

(50)