Determinarea indicelui de refractie al unui lichid. aberatiile lentilelor.

DETERMINAREA INDICELUI DE REFRACTIE AL UNUI LICHID. ABERATIILE LENTILELOR.

1. Scopul lucrarii

In aceasta lucrare se determina experimental indicele de refractie al unui lichid, prin masurarea distantei focale a sistemului optic obtinut prin inversarea unei lentile in acel lichid. De asemenea, se analizeaza precizia metodei in functie de erorile care apar in determinarea imaginii unui obiect punctiform datorita aberatiilor lentilelor.

2. Teoria lucrarii

Indicele de refractie absolut n al unui mediu este raportul dintre viteza de propagare c a luminii in vid si viteza de propagare v a luminii in mediul considerat:

.

Indicele de refractie relativ reprezinta raportul dintre indicele de refractie absolut al mediului 2 si indicele de refractie absolut al mediului 1. Valoarea indicelui de refractie depinde de natura mediului respectiv, de lungimea de unda a luminii care se propaga prin acel mediu, de temperatura si de directia de propagare in cazul mediilor anizotrope.

2. 1. Formarea imaginii prin refractie pe suprafete sferice (dioptrul sferic)

Un obiect luminos punctiform S aflat intr-un mediu cu indicele de refractie , formeaza in mediul al doilea cu indicele de refractie o zona luminoasa de o anumita largime care, in aproximatie paraxiala devine un punct imagine (fig. 1).

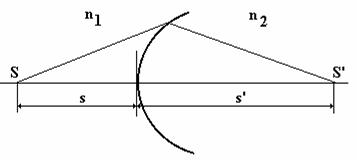
Fig. 1

Daca este raza de curbura a suprafetei care separa cele doua medii, pozitiile obiectului, respectiv imaginii sunt legate prin relatia

, (1)

unde s si sunt distantele definite in Fig. 1. Imaginea este virtuala atunci cand este negativ si reala cand este pozitiv.

2. 2. Formarea imaginii printr-o lentila

Consideram lentila ca fiind formata din doi dioptri sferici de raze si , iar indicele de refractie al materialului lentilei este . Daca lentila se afla intr-un mediu cu indice de refractie (aer), refractia la suprafata primului dioptru produce imaginea obiectului punctiform , aflat la distanta s, in punctul , aflat la distanta de varful dioptrului. Relatia (1) devine

(2)

Imaginea obtinuta localizata la distanta de suprafata celui de-al doilea dioptru sferic devine obiect pentru acesta iar pozitia imaginii finale este data de relatia

(3)

Din relatiile (2) si (3) se obtine:

, (4)

unde este distanta focala a lentilei.

Relatia (4) este adevarata numai in cazul in care dimensiunile lentilei sunt mici in comparatie cu razele de curbura si, deci, cu distanta focala a lentilei iar punctul obiect este foarte aproape de axa optica a sistemului. In caz contrar, imaginea este afectata de aparitia unei aberatii geometrice datorita formei sferice a suprafetei optice utilizate si care are ca efect faptul ca unui obiect punctiform ii corespunde o zona spatiala si nu o imagine punctiforma.

2. 3. Aberatiile lentilelor

In aproximatia gaussiana care presupune fascicule inguste, invecinate cu axa sistemului optic, imaginea unui obiect este buna daca indeplineste trei conditii, si anume, daca este: stigmatica, plana si ortoscopica.

Imaginea stigmatica este o imagine precisa, in care fiecarui punct-obiect ii corespunde un punct imagine.

Imaginea plana este atunci cand fiecarui obiect-plan, perpendicular pe axa optica ii corespunde o imagine plana, de asemenea perpendiculara pe axa optica.

Imaginea ortoscopica este imaginea nedeformata, asemenea obiectului, indiferent de locul considerat in planul imagine. Orice abatere de la stigmatism, planeitate sau ortoscopie se numeste aberatie. In cele ce urmeaza a fost aleasa una din clasificarile posibile ale aberatiilor in cazul lentilelor.

Aberatiile lentilelor:

- fascicul           - fascicul axial: Aberatia de sfericitate

larg - fascicul inclinat: Coma

1. geometrice

(radiatii monocromatice,

indice de refractie constant)         - obiect punctiform extraaxial:

- fascicul Astigmatism

inclinat Curbura campului imagine

- obiect plan perpendicular pe ax:

Distorsiune

2. cromatice

(radiatii policromatice, indicele de refractie creste monoton cu scaderea lungimii de unda)

2. 4. Principiul metodei de determinare a indicelui de refractie al unui lichid

Distanta focala a unui sistem de lentile subtiri se poate calcula cu ajutorul relatiei:

, (5)

unde este distanta focala a fiecarei lentile din sistem.

Daca o lentila biconvexa de distanta focala este introdusa intr-o cuva cu lichid de indice de refractie , se formeaza un sistem de lentile a carui distanta focala este

. (6)

Exprimand in functie de distanta focala a lentilei cu indicele de refractie se obtine expresia

. (7)

Determinarea distantei focale a sistemului de lentile va permite calculul indicelui de refractie al lichidului.

Precizia metodei poate fi mult mai marita daca obiectul este plasat in apropierea focarului lentilei. Intr-adevar, din relatia (4) obtinem

(8)

si

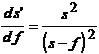^. (9)

Deci, plasand obiectul luminos in apropierea focarului termenul devine foarte mic si foarte mare. O variatie foarte mica a distantei focale va produce o variatie sensibila a pozitiei imaginii.

Aberatiile geometrice si cromatice ale lentilei conduc la existenta unei erori in determinarea distantei la care se formeaza imaginea. Daca presupunem ca marimea acestei erori este , atunci eroarea in determinarea distantei focale va fi data de relatia

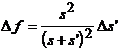, (10)

si eroarea relativa de determinare a distantei focale a lentilei este:

. (11)

Minimul erorii relative este dat de minimul functiei .

3. Descrierea instalatiei experimentale

Instalatia experimentala este prezentata in figura 2, unde elementele constituente reprezinta:

A - sursa de lumina

B - lentila

C - orificiu cu fir reticular

D - cuva cu lentila

E - firul galben cu diafragma de diferite marimi

F - ecran de vizualizare a imaginii.

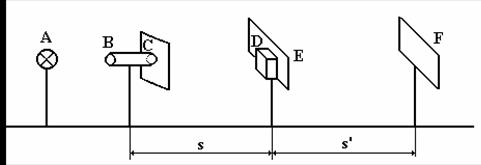
Fig. 2

4. Modul de lucru

4. 1. Folosind bancul optic din figura 2 se gasesc distantele si pentru care imaginea obiectului (firul reticular) apare clar pe ecran, atunci cand cuva este fara apa.

4. 2. Se umple cuva cu apa si se gasesc noile distante s si pentru care se obtine imaginea clara a firului reticular pe ecran.

4. 3. Se modifica pozitia ecranului, determinandu-se (intervalul in care imaginea firului reticular pe ecran poate fi considerata suficient de clara).

5. Indicatii privind prelucrarea datelor experimentale

Cu ajutorul datelor experimentale obtinute la punctul 4 al lucrarii:

5. 1. se verifica experimental formula lentilelor, stiind ca distanta focala a lentilei de sticla este 4 cm;

5. 2. se calculeaza indicele de refractie al apei determinand distanta focala a sistemului de lentile format prin umplerea cuvei cu apa;

5. 3. se determina abaterea standard asupra valorii medii a indicelui de refractie al apei;

5. 4. se calculeaza eroarea relativa de determinare a distantei focale a lentilei.

6. Intrebari

1. De ce s-a utilizat filtru galben si nu lumina alba ?

2. De ce nu s-a folosit ca obiect chiar filamentul becului ?

3. Cum poate fi imbunatatita metoda de determinare a indicelui de refractie ?