ELEMENTE DE TERMODINAMICA - Postulatele termodinamicii

ELEMENTE DE TERMODINAMICA

1.1.     INTRODUCERE

Corpurile macroscopice sunt formate din atomi si molecule, constituenti microscopici, ce se afla in continua miscare, numita miscare de agitatie termica.

Descoperirea masinii cu vapori (J. Watt 1770) a condus in secolul XIX la studiul relatiilor dintre fenomenele calorice si cele mecanice, deci la studiul conditiilor de transformare a caldurii in lucru mecanic. Din acest studiu se naste termodinamica, care studiaza problemele fundamentale ale sistemelor fizice la scara macroscopica, stabilind relatii cantitative intre marimile direct observabile, cum ar fi presiunea, volumul, temperatura, fara a lua in considerare structura interna.

Rapid termodinamica a depasit cadrul pentru care fusese creata initial si evolutia sa a fost foarte rapida. Astfel in 1850 s-au enuntat primele doua principii ale termodinamicii, primul de catre R. Mayer, care generalizeaza conceptul de energie, si al doilea, sub diverse forme, de catre S. Carnot, R. Clausius si J. Thomson, principiu care introduce entropia.

Termodinamica moderna are doua directii principale de actiune: termodinamica fenomenologica si cea statistica. Termodinamica fenomenologica introduce o serie de notiuni si concepte fundamentale fara a tine seama de structura interna a corpurilori. Termodinamica statistica porneste de la structura microscopica de atomi si molecule, constituenti aflati intr-o perpetua miscare dezordonata. Parametrii microscopici, cum ar fi: masa, viteza, energia medie a constituentilor, determina parametrii macroscopici amintiti mai sus. Avand in vedere ca un sistem fizic este constituit dintr-un numar foarte mare de constituenti microscopici nu se poate vorbi decat de o anumita probabilitate de realizare a unei stari microscopice, stabilite pe baza teoriei probabilitatilor.

1.1.1.             Notiuni fundamentale

Vom numi sistem termodinamic o regiune a universului delimitata astfel ca obiectele macroscopice continute in ea sa interactioneze cu mediul extern ca un intreg.

Un sistem termodinamic se numeste izolat, daca nu schimba nici energie nici substanta cu exteriorul. Un sistem termodinamic va fi numit inchis daca nu schimba substanta cu exteriorul (pot exista schimburi energetice).

Ansamblul proprietatilor unui sistem termodinamic la un anumit moment, poarta numele de stare. Legat de notiunea de stare a unui sistem se introduce si notiunea de functie de stare. Aceasta reprezinta o marime ce depinde de grupul complet al parametrilor ce definesc starea sistemului.

Daca parametrii ce definesc starea sistemului nu variaza in timp starea se numeste stationara. Daca in plus nu exista fluxuri externe care sa implice transport de substanta, starea se numeste de echilibru termodinamic.

In general, pentru descrierea unei stari termodinamice se utilizeaza un numar minim de parametrii independenti. Acesti parametri pot fi: externi (campul gravitational) cand depind de coordonatele corpurilor exterioare sistemului, sau interni (presiunea) cand depind atat de coordonatele corpurilor externe sistemului cat si de valorile medii ale coordonatelor si vitezelor constituientilor sistemului.

Parametrii pot fi de asemenea: mecanici (volum, presiune) si termodinamici (temperatura, energie interna).

Din punct de vedere al aplicatiilor ce vor urma este interesanta clasificarea parametrilor in extensivi ce depind de marimea sistemului (volum, numar de particule) si intensivi care nu depind de marimea sistemului (presiune, temperatura). In cele ce urmeaza vom defini mai precis notiunile introduse.

O marime X, asociata unui sistem, este extensiva daca putem defini o densitate volumica x_v=d X/ dV, unde dX este cantitatea din marimea X continuta in elementul de volum dV. Cantitatea X continuta in sistemul de volum V este atunci:

Variatia X, intre doua momente t₁ si t₂ a marimii extensive a unui sistem, delimitat printr-o suprafata S, comporta doua contributii:

- prima provine din schimbul cu mediul exterior. Este contributia X_p primita de sistem. Daca X_p >0 marimea este efectiv primita de sistem, iar daca X_p<0 marimea este furnizata mediului exterior.

- a doua, X_prod , este produsa de sistem. Daca X_prod >0 are loc aparitia marimii, iar daca X_prod are loc disparitia marimii respective. In concluzie:

X=X_p+ X_prod

Referitor la marimile extensive se poate introduce relatia:

(1.1)

unde este vectorul curent volumic al marimii X si este productia marimii X pe unitatea de volum si unitatea de timp. Relatia (1.1) se numeste ecuatia de continuitate relativa la marimea extensiva X.

O marime este conservativa daca ea nu poate fi nici creata si nici distrusa, indiferent de evolutia sistemului.

Atunci cand parametrii sistemului variaza in timp, in sistemul considerat are loc un proces. Dupa natura starilor intermediare procesele termodinamice pot fi: cuasistatice si nestatice. Un proces este numit cvasistatic daca evolutia in timp a parametrilor sistemului este atat de lenta incat toate starile intermediare sa poata fi considerate stari de echilibru. Daca parametrii sistemului evolueaza rapid, astfel ca starile intermediare sa nu poata fi caracterizate termodinamic, procesul este nestatic.

Revenirea spontana a sistemului in starea de echilibru atunci cand actiunea ce a produs iesirea sa din aceasta stare inceteaza, se numeste proces de relaxare. Timpul in care are loc aceasta revenire la starea de echilibru se numeste timp de relaxare.

O alta clasificare imparte procesele termodinamice in reversibile (sensul desfasurarii sale poate fi inversat.) si ireversibile (sensul procesului nu poate fi inversat). Orice proces reversibil este cuasistatic.

1.1.2. Postulatele termodinamicii

In termodinamica se introduce urmatorul principiu (principiul general al termodinamicii):

Un sistem termodinamic izolat evolueaza spre starea de echilibru pe care o atinge fara a o putea depasi, atat timp cat parametrii externi sunt mentinuti constanti.

Principiul de mai sus fixeaza si limitele de aplicabilitate ale termodinamicii. Termodinamica este aplicabila unor sisteme care au un numar mare de elemente, dar nu infinit.

Principiul zero al termodinamicii (tranzitivitatea echilibrului termodinamic).

Consideram doua sisteme A si B separate printr-un perete adiabatic (nu permite schimbul de caldura). Daca cele doua sisteme sunt puse in contact cu un al treilea sistem C, sistemele A si C precum si B si C evolueaza spre o noua stare de echilibru comuna. Separand sistemele A si B de sistemul C si punandu-le in contact termic se constata ca cele doua sisteme sunt in echilibru termic. Prin urmare echilibrul termodinamic este tranzitiv.

O consecinta importanta a acestui principiu este aceea ca starea de echilibru a unui sistem este determinata nu numai de catre parametrii externi ci si de un parametru intern, acelasi pentru toate punctele sistemului, parametru ce a fost numit temperatura. Temperatura este deci o functie de stare a echilibrului termodinamic. Deci starea echilibru a unui sistem este functie de parametrii externi si de temperatura.

O formulare echivalenta a principiului zero al termodinamicii este urmatoarea:

Toti parametrii interni ai sistemului sunt functii de parametrii externi si de temperatura.

Din principiul zero al termodinamicii se poate deduce ca temperetura unui sistem in echilibru termodinamic este o functie de parametrii externi si interni:

unde prin A_i si respectiv a_i am notat parametrii externi si respectiv interni. O relatie de acest tip se numeste ecuatie termica de stare.

Deducerea proprietatilor macroscopice din cele microscopice se simplifica pentru un sistem cu o structura microscopica mai simpla, cum este gazul perfect sau ideal. Acest sistem are urmatoarele proprietati esentiale:

sistemul este format dintr-un numar foarte mare de constituenti de aceeasi natura (atomi, molecule) care se misca complet dezordonat;

ciocnirea intre constituenti cat si cu peretii incintei este perfect elastica, deci viteza in modul inainte si dupa ciocnire are aceeasi valoare;

dimensiunile constituentilor sunt mici in comparatie cu distanta dintre ei, acestia fiind punctiformi si pot avea numai o miscare de translatie nu si de rotatie;

distanta dintre constituenti este suficient de mare incat interactiunile dintre acestia sa fie neglijabile, adica energia potentiala U = 0;

distributia vitezelor constituentilor nu se modifica in timp, aceasta inseamna ca numarul moleculelor care au o anumita valoare a vitezei este intotdeauna aceasi.

Energia unui gaz monoatomic perfect, aflat in repaus din punct de vedere macroscopic, este data de suma energiilor cinetice al particulelor constituente. Aceasta energie se numeste energie inerna:

Cum moleculele unui gaz perfect sunt identice putem spune ca suma reprezinta de N ori valoarea medie a patratului vitezelor particulelor:

unde este viteza patratica medie. Se obtine astfel:

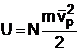(1.2)

Pornind de la relatia (1.2) se poate defini temperatura cinetica T a unui gaz perfect monoatomic prin relatia:

(1.3)

unde k_B este constanta Boltzmann (k_B=1,38 10^-23 J/K).

Miscarea unei molecule este caracterizata in mod univoc de un numar de f parametri independenti numiti grade de libertate. Miscarile pot fi, insa, limitate de un numar l de restrictii numite legaturi, astfel ca, pentru un sistem format din N molecule, numarul de grade de libertate f se va micsora, fiind dat de formula: f 3N − l

Teorema de echipartitie a energiei dupa gradele de libertate stabileste ca fiecarui grad de libertate al moleculei unui gaz ii corespunde o energie medie

(1.4)

Astfel energia interna a gazului (suma tuturor tipurilor de energie pe care le poseda toate moleculele gazului, precum si energia de interactiune a acestora cu eventualele campuri exterioare) este:

(1.5)

Se poate introduce presiunea exercitata de un fluid ca forta ce actioneaza pe unitatea de suprafata. Pentru un gaz, interpretarea microscopica data de Bernoulli in 1873, conduce la concluzia ca originea presiunii unui gaz asupra unui perete este ciocnirea moleculelor gazului de peretele respectiv. S-a aratat ca valoarea presiunii unui gaz poate fi exprimata prin relatia:

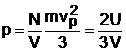(1.6)

unde V este volumul ocupat de gaz.

Introducand relatia (1.5) in (1.6) si inlocuind n_v=N/V, se obtine ecuatia de stare a gazului perfect, ecuatie ce leaga presiunea, volumul si temperatura:

(1.7)

sau exprimand in functie de numarul de moli si de constanta R obtinem:

p V=n R T (1.8)

unde n=N/N_A, N_A fiind numarul lui Avogadro si R= N_Ak_B =8,314 J /K mol.

Pornind de la ecuatia de stare se pot regasi legile simple ale gazului ideal, pe care le vom reaminti in continuare.

1. Legea lui R. Boyle si E. Mariotte : pentru aceeasi masa de gaz la temperatura constanta, produsul p V dintre presiune si volum este constant.

2. Legea lui Avogadro : volume egale de gaze perfecte aflate in aceeasi conditii de presiune si temperatura, contin acelasi numar de moli.

3. Legea lui L. Gay-Lussac : La presiune constanta, volumul ocupat de o cantitate data de gaz perfect este proportional cu temperatura absoluta.

4. Legea lui J. Charles : la volum constant, presiunea unei cantitati determinate de gaz perfect este proportionala cu temperatura absoluta.

5. Legea lui Dalton : considerand un amestec de doua gaze perfecte intr-un volum V si la aceeasi temperatura T, putem scrie : p₁V=n₁RT si p₂V=n₂RT. Daca admitem ca intre molecule nu exista interactiune, ansamblul formeaza tot un gaz perfect pentru care pV=(n₁+n₂) RT. Rezulta deci :

(1.9)

relatie ce reprezinta legea lui Dalton.

6. Prima lege a lui Joule : energia interna a unui gaz perfect nu depinde decat de temperatura sa.

Pentru concentratii mici, gazele reale satisfac proprietatile gazului ideal. Cand concentratiile cresc, nu mai este permisa neglijarea interactiunilor care se manifesta la distante mari fata de dimensiunile moleculelor si nici neglijarea volumului propriu al moleculelor.

J. D. van der Walls a dedus o noua ecuatie de stare, care ia in considerare factorii enumerati. Se considera ca moleculele au o forma sferica rigida cu diametrul d. Daca reprezinta volumul molar al gazului ideal, atunci, in cazul gazului real volumul se va micsora, devenind (v-b) unde b reprezinta volumul propriu al moleculelor. In consecinta presiunea va creste, deoarece o reducere a volumului conduce la cresterea numarului de ciocniri a moleculelor cu peretii.

Introducand factorii de corectie aupra presiunii si volumului, ecuatia de stare pentru un mol de gaz se va scrie:

(1.10)

unde a si b reprezinta constante dependente de natura gazului care se determina experimental. Corectia constitue o presiune suplimentara ce apare datorita interactiunii dintre molecule. In cazul gazului ideal, izotermele (pV=const.) sunt hiperbole echilaterale. Pentru gazul van der Waals presiunea variaza cu volumul dupa legea:

(1.11)

Cand volumul molar v descreste, presiunea creste. Cum descreste mai rapid, la o temperatura suficient de joasa, presiunea trece printr-un maxim. Cand volumul v descreste mai departe, presiunea trece printr-un minim, apoi creste nelimitat.

Cu cresterea temperaturii punctele de maxim si de minim sunt tot mai putin evidentiate si mai aproape de punctul inflexiune care se afla intre ele. La o anumita temperatura , numita temperatura critica, ele coincid intr-un punct de inflexiune, numit punct critic. Pentru izotermele van der Waals nu mai prezinta puncte de inflexiune si tind catre comportarea de tip hiperbola a izotermelor gazului real.