
|
|
|
ELEMENTE DE TEORIA STABILITATII FLUIDELOR
Problema stabilitatii miscarilor fluidelor s-a pus practic in paralel cu aceea a mecanicii fluidelor. Experientele lui G. Hagen (1839) si J. Poisenille (1841), ca si cele ale lui O. Reynolds (1883) reprezinta punctul de plecare al studiilor legate de stabilitatea miscarii. Printre precursori mai mentionam pe H. Helmholtz (1848) care analizeaza suprafetele de discontinuitate ale vitezei in miscari stratificate si Tyndal (1867) care studiaza instabilitatea de tip Helmholtz la frontiera unui jet de aer circular.
Cel care a pus bazele problemei clasice a stabilitatii hidrodinamice sub actiunea unor perturbatii mici a fost J.W. Strutt (Lord Rayleigh) in 1880. In 1895, O. Reynolds analizeaza transferul de energie, punand bazele unei a doua metode (cea energetica) in studiul stabilitatii miscarii. In anii 1907 - 1908, McF. Orr si A. Sommerfeld au dedus pentru miscari paralele, ecuatia care le poarta numele, pentru perturbatii de forma:
![]() (1)
(1)
denumite unde transversale Tollmien - Schlichting, dupa numele celor care au utilizat primii asemenea forme de perturbatii in studiul stabilitatii. Succese remarcabile in studiul stabilitatii miscarilor la mici perturbatii se datoresc lui G.I. Taylor (1923), W. Heisenberg (1924) in analiza curgerii plane Poisenille. Pentru stabilitatea miscarii in stratul limita mentionam cercetarile lui L. Prandtl (1921), O. Tiejens (1925), W. Tallmien (1929).
In lucrarile elaborate de Chandrashekhar, S.(1961), Drazin, P.G. (1981), Josep, D.D. (1976), Li, W.H, Lam, S.H. (1964), Shaw, M. (1964), Staniukovici, K.P. (1960) sunt dezvoltate studii privind teoria clasica a stabilitatii hidrodinamice.
2 Teoreme de stabilitate. Criterii de stabilitate
Pentru sistemele liniare, studiul stabilitatii miscarii se refera la studiul semnului radacinilor ecuatiei caracteristice atasata ecuatiilor diferentiale ale miscarii perturbate [31, 49]:
![]() (46)
(46)
In
ipoteza ![]() , conditia necesara, dar nu si
suficienta, ca ecuatia algebrica (46) sa aiba
radacini reale negative sau radacini complex conjugate cu
parti reale negative ( conditii de stabilitate a
miscarii), este ca toti coeficientii
, conditia necesara, dar nu si
suficienta, ca ecuatia algebrica (46) sa aiba
radacini reale negative sau radacini complex conjugate cu
parti reale negative ( conditii de stabilitate a
miscarii), este ca toti coeficientii ![]() sa fie pozitivi.
sa fie pozitivi.
2.1 Criteriul de stabilitate Routh - Hurwitz
Presupunand
conditia ![]() , (k = 0, 1,., n) in (1) criteriul Routh-Hurwitz are
urmatorul enunt: conditia necesara si suficienta
ca ecuatia caracteristica (1) sa aiba radacini
reale negative sau complex conjugate cu partile reale negative, este
ca toti determinantii Hurwitz Dk,
, (k = 0, 1,., n) in (1) criteriul Routh-Hurwitz are
urmatorul enunt: conditia necesara si suficienta
ca ecuatia caracteristica (1) sa aiba radacini
reale negative sau complex conjugate cu partile reale negative, este
ca toti determinantii Hurwitz Dk, ![]() , formati cu coeficientii ecuatiei
caracteristice sa fie pozitivi, adica [31, 49
, formati cu coeficientii ecuatiei
caracteristice sa fie pozitivi, adica [31, 49
![]() ;
; 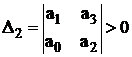 ,
,
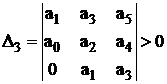 , . . .,
, . . ., 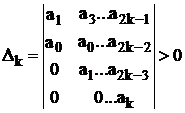 (47)
(47)
Pentru ecuatii caracteristice de gradul trei avem conditiile
![]() ,
, ![]() ,
, ![]() (48)
(48)
iar pentru cele de gradul patru:
![]() ;
; ![]() ,
,
![]() ;
; ![]() (49)
(49)
In cazul sistemelor cu ![]() , calculele devin
laborioase, fapt pentru care se recomanda metode geometrice legate de
criteriul de stabilitate Mihailov.
, calculele devin
laborioase, fapt pentru care se recomanda metode geometrice legate de
criteriul de stabilitate Mihailov.
2.2 Criteriul de stabilitate Mihailov
![]() ,
, ![]() .
.
Enuntul criteriului: pentru ca toate
radacinile ecuatiei caracteristice (46) sa aiba parte
reala negativa, este necesar si suficient ca la variatia
continua a lui y de la zero la ![]() , vectorul
, vectorul ![]() , reprezentat cu originea in originea axelor (
, reprezentat cu originea in originea axelor (![]() ), sa se roteasca in sens trigonometric cu unghiul
), sa se roteasca in sens trigonometric cu unghiul ![]() .
.
2.3 Metoda Liapunov. Functia lui Liapunov
Se
considera cazul sistemelor cu doua grade de libertate. Studiul
stabilitatii miscarii se face cu ajutorul unei functii
reale 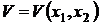 - denumita
functia lui Liapunov, definita intr-o vecinatate a pozitiei
de echilibru (
- denumita
functia lui Liapunov, definita intr-o vecinatate a pozitiei
de echilibru (![]() ,
,![]() ), cu
), cu
![]() ,
, ![]() ,
, ![]() mic si pozitiv,
care are urmatoarele proprietati:
mic si pozitiv,
care are urmatoarele proprietati:
1) Derivata totala a lui ![]() in punctul de echilibru
(
in punctul de echilibru
( ![]() ,
,![]() ) este nula,
) este nula,
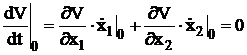 . (51)
. (51)
2) Daca ![]() este pozitiv
definita atunci graficul lui
este pozitiv
definita atunci graficul lui ![]() este o curba
inchisa ce contine originea coordonatelor.
este o curba
inchisa ce contine originea coordonatelor.
Daca ![]() , atunci graficul lui
, atunci graficul lui ![]() este dispus in
interiorul curbei
este dispus in
interiorul curbei ![]() si graficele nu
au puncte comune.
si graficele nu
au puncte comune.
2.4 Teorema lui Liapunov
Daca ecuatiilor diferentiale
ale miscarii perturbate se ataseaza o functie ![]() , definita ca semn ( plus sau minus), cu proprietatea
, definita ca semn ( plus sau minus), cu proprietatea ![]() definita ca semn,
dar de semn opus lui
definita ca semn,
dar de semn opus lui ![]() sau
sau ![]() , atunci miscarea neperturbata este stabila.
, atunci miscarea neperturbata este stabila.
Daca in enuntul teoremei lui Liapunov se
renunta la conditia ![]() ,atunci miscarea neperturbata este asimptotic
stabila.
,atunci miscarea neperturbata este asimptotic
stabila.
2.7 Ecuatiile primei aproximari pentru sisteme autonome
Sistemului dinamic autonom
![]() ,
,
![]() , (56)
, (56)
i se asociaza sistemul liniar
![]()
![]() (57)
(57)
denumit sistemul ecuatiilor primei aproximari, care, in multe situatii, da indicatii exacte asupra stabilitatii miscarii neperturbate. In acest sens se utilizeaza doua teoreme ale lui Liapunov:
(I)
Daca partile reale ale
tuturor radacinilor ecuatiei caracteristice atasata
sistemului primei aproximari (57) sunt negative, atunci solutia
nula a sistemului autonom (56)
(miscarea neperturbata) este asomptotic stabila, indiferent de
forma termenilor neliniari ![]() ,
, ![]() ;
;
(II)
Daca cel putin una din partile reale ale unei
radacini a ecuatiei caracteristice atasata sistemului
primei aproximari (57), este pozitiva, atunci solutia nula
a sistemului autonom (56) (miscarea neperturbata) este
nestabila, indiferent de forma termenilor neliniari![]() ,
, ![]() .
.
2.8 Stabilitate absoluta. Criteriul lui V.M. Popov
Se presupune ca ecuatiile diferentiale ale miscarii perturbate au forma:
![]() ,
,
![]() , (58)
, (58)
unde ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() , si
, si ![]() sunt constante.
sunt constante.
Fie ![]() functie
neliniara pentru care solutia
nula a sistemului (58) este stabila (miscarea
neperturbata este stabila). In virtutea continuitatii,
aceasta solutie va fi stabila pentru o multime de
functii ale caror grafice sunt dispuse in vecinatatea graficului
functiei
functie
neliniara pentru care solutia
nula a sistemului (58) este stabila (miscarea
neperturbata este stabila). In virtutea continuitatii,
aceasta solutie va fi stabila pentru o multime de
functii ale caror grafice sunt dispuse in vecinatatea graficului
functiei ![]() (fig. 1). Graficele
tuturor acestor functii in planul
(fig. 1). Graficele
tuturor acestor functii in planul ![]() se afla intre
doua drepte:
se afla intre
doua drepte:
![]() ,
,![]() , cu
, cu ![]() .
.
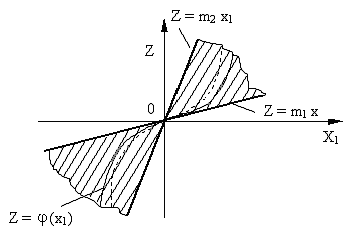
Fig. 1 Graficul ![]() in domeniul de stabilitate
in domeniul de stabilitate
3 Stabilitatea unei miscari laminare cunoscute
Sa consideram ca avem o anumita
miscare laminara si ca dorim sa stim daca aceasta
miscare este stabila sau nu. Miscarea considerata,
denumita miscare de baza, va fi caracterizata printr-un
camp de viteze ![]() si presiuni
si presiuni ![]() va satisface sistemul
de ecuatii (68) si (69) cu conditii initiale si la
limita corespunzatoare, respectiv:
va satisface sistemul
de ecuatii (68) si (69) cu conditii initiale si la
limita corespunzatoare, respectiv:
![]() ,
(71)
,
(71)
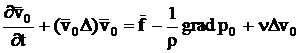 (72)
(72)
![]() , (73)
, (73) ![]() , (74)
, (74)
unde relatiile (73), (74 reprezinta formal conditiile initiale si respectiv la limita, (e) reprezentand o suprafata solida la care fluidul adera, adica fluidul sa aiba viteza suprafetei pe aceasta.
Presupunem o miscare perturbata caracterizata prin viteze si presiuni diferite:
![]() .. (75)
.. (75)
Miscarea de baza poate fi perturbata prin mecanisme diferite, dintre care mentionam:
- frontierele solide se pot deplasa sau modifica (oscilatii sau deformatii);
- injectie de fluid;
- conditii la infinit variabile sau variatia conditiilor la limita.
Din punctul de vedere al stabilitatii in sensul lui Liapunov intereseaza in primul rand posibilitatea de modificare a miscarii datorita modificarii conditiilor initiale (6). Se va studia miscarea (8) care rezulta din modificarea conditiilor initiale prin impunerea unor perturbatii initiale. In aceste conditii miscarea este caracterizata de urmatoarele ecuatii si conditii:
![]() (76)
(76)
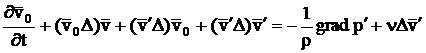 (77)
(77)
![]() (78)
(78)
![]() . (79)
. (79)
Problema determinarii miscarii
perturbate revine la a gasi ![]() din sistemul (76) (79), unde
din sistemul (76) (79), unde ![]() si
si ![]() sunt cunoscute.
sunt cunoscute.
Formularea matematica a conditiilor de stabilitate, in sensul lui Liapunov, este urmatoarea:
"miscarea este stabila daca pentru un numar pozitiv e>0 exista un alt numar pozitiv d > 0, eventual depinzand de e, astfel incat:
![]() (80)
(80)
cand:
![]() (81)
(81)
sau altfel notat:
![]() (81
(81
unde cu ![]() s-a notat norma unui camp scalar sau
vectorial, definita prin:
s-a notat norma unui camp scalar sau
vectorial, definita prin:
![]() (82)
(82)
in tot domeniul miscarii D.
Conditia de stabilitate asimptotica, in sensul lui Liapunov va fi:
![]() cand
cand ![]() (83)
(83)
Daca nu se indeplinesc conditiile (81) (83) atunci miscarea va fi instabila.
2 Miscari paralele de baza si perturbate
Miscarile paralele reprezinta o clasa de miscari fara forte de inertie. Asemenea miscari se pot realiza intr-un strat de fluid de grosime constanta marginit de suprafete solide plane si paralele, miscari realizate fie prin deplasarea suprafetelor cu o viteza relativa una fata de alta (miscari de tip Couette), fie datorita unui gradient de presiune (miscari de tip Poisenille), fie prin combinarea celor doua miscari precedente [7, 16, 31, 49, 89, 109].
Fie x, z coordonatele carteziene care definesc un plan paralel cu suprafetele solide si fie y coordonata normala pe aceasta. Miscarea de baza paralela stationara este caracterizata prin componentele vitezei in directiile x si z:
![]() (94)
(94)
In aceste conditii, ecuatiile Navier-Stokes (5) se scrie sub forma:
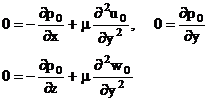 (95)
(95)
Ecuatia de continuitate si forma vectoriala a ecuatiilor
Navier-Stokes in marimi adimensionale
Ecuatia de continuitate si forma vectoriala a ecuatiilor Navier-Stokes se pot scrie in marimi adimensionale:
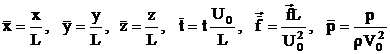 (101)
(101)
unde L este o valoare caracteristica pentru lungimi, iar U0 pentru viteze. Se mai noteaza:
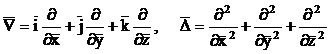 (102)
(102)
iar sistemul (99), (100) se scrie sub forma adimensionala:
![]() (103)
(103)
![]() (104)
(104)
unde:
![]() este numarul Reynolds. (105)
este numarul Reynolds. (105)
Miscarea perturbata
Se considera o miscare de baza paralela peste care se suprapun perturbatiile u , v , w , p . N marimi adimensionale, cu notatii fara bare,
Perturbatiile vor satisface sistemul:
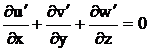 (106)
(106)
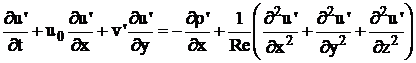 (107)
(107) 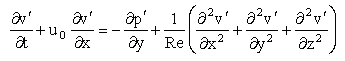 (108)
(108)
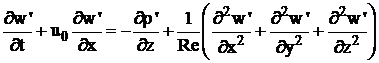 . (109)
. (109)
Pe cele doua suprafete solide plane (y = 0,1) perturbatiile vitezei se considera nule.
Sistemul (106) (109) admite solutii de forma:
![]() (110)
(110)
![]() (111)
(111)
![]() (112)
(112)
![]() , (113)
, (113)
unde functiile
amplitudine ![]() sunt marimi complexe; a b si c sunt de asemeni marimi complexe.
sunt marimi complexe; a b si c sunt de asemeni marimi complexe.
Notam cu D = d/dy, D2 = d2/d2y, introducem relatiile (110) (113) in ecuatiile sistemului (106) (109) si deducem sistemul:
![]() , (114)
, (114)
![]() , (115)
, (115)
![]() , (116)
, (116)
![]() , (117)
, (117)
cu mentiunea ca pe
suprafetele solide plane amplitudinile ![]() sunt nule.
sunt nule.
C.C. Lin transforma sistemul (114) . (117) intr-un sistem omogen de sase ecuatii de ordinul intai cu sase necunoscute, cuprinse in matricea coloana (X):
![]() . (118)
. (118)
Forma matriceala a sistemului omogen (114) (117) este:
![]() , (119)
, (119)
unde ![]() , A fiind
matricea patrata:
, A fiind
matricea patrata:
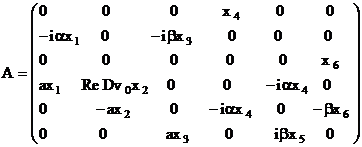 (120)
(120)
unde: ![]() . Pe
suprafetele solide plane ce delimiteaza fluidul avem:
. Pe
suprafetele solide plane ce delimiteaza fluidul avem:
x1 = x2 = x3 = 0.
Caracterizare a stabilitatii dupa H.B. Squire
O prima caracterizare a stabilitatii unei miscari de baza paralela si plana se obtine prin urmarirea evolutiei unor perturbatii bidimensionale.
Este valabila astfel teorema lui Squire:
"pentru o miscare paralela
bidimensionala caracterizata printr-o distributie de viteze ![]() cel mai mic numar
Raynolds critic apare pentru cazul unor perturbatii bidimensionale care se
propaga in aceeasi directie x cu vitezele din miscarea de
baza".
cel mai mic numar
Raynolds critic apare pentru cazul unor perturbatii bidimensionale care se
propaga in aceeasi directie x cu vitezele din miscarea de
baza".
Ecuatia Orr-Sommerfeld
Se adopta perturbatiile de forma:
![]() , (125)
, (125)
![]() , (126)
, (126)
![]() , (127)
, (127)
denumite undele transversale Tallmien-Schlichting.
Pentru t finit fronturile de unda sunt suprafete cilindrice cu generatoarele paralele cu axa Oz, perpendiculare pe planul miscarii de baza.
Pentru determinarea perturbatiilor (125) (127),
avem de rezolvat sistemul de trei ecuatii cu necunoscutele ![]() :
:
![]() , (128)
, (128)
![]() , (129)
, (129)
![]() , (130)
, (130)
cu conditiile la
limita u = 0, v = 0 pe cele
doua suprafete frontiera, sau sistemul de patru ecuatii cu
patru necunoscute dedus din (114) (117) cu ![]() .
.
Sistemul (128) (130) este liniar, fapt care permite
eliminarea a doua din cele trei necunoscute (![]() ), forma cea mai simpla fiind:
), forma cea mai simpla fiind:
![]() , (131)
, (131)
cunoscuta sub numele de ecuatia Orr-Sommerfeld.
6.1 Problema nevascoasa
Unele rezultate se pot deduce studiind problema nevascoasa cu inlocuirea profilelor de viteze cu unele liniare pe portiuni. Se considera trei tipuri de variatii liniare [7, 16, 31, 49, 89, 109]:
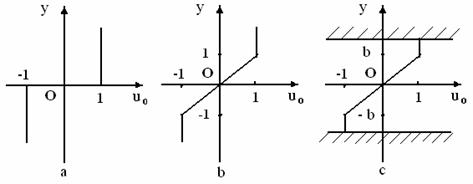
Fig. 2 Miscari de baza cu viteze liniare pe portiuni
Cazul
(a) aproximeaza miscarea in prezenta unui strat de vartejuri,
distributia din (b) inlocuieste un strat de forfecare de grosime
finita in fluid nelimitat iar cel din (c) aproximeaza un strat de
forfecare marginit de doua suprafete de fluid limitat. Se impune
deducerea unei conditii de racordare pentru punctele in care u0
sau ![]() prezinta o
discontinuitate.
prezinta o
discontinuitate.
Prima conditie de racordare:
![]() . (150)
. (150)
A doua conditie de racordare se deduce din
aspectul fizic de inexistenta a unui salt de presiune, scriind
relatia (137) pentru ![]() sub forma:
sub forma:
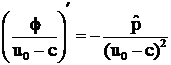 , (151)
, (151)
Miscarea
este instabila sub forma unor unde stationare ce cresc
proportional cu ![]() .
.
Pentru cazul din fig. 2.b,
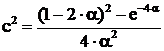 (155) Din
(155) Din
![]() obtinem
solutia
obtinem
solutia ![]() , iar pentru
, iar pentru ![]() rezulta ci > 0 ceea ce conduce la instabilitate. Gradul maxim de
amplificare
rezulta ci > 0 ceea ce conduce la instabilitate. Gradul maxim de
amplificare ![]() se
se
obtine ![]() .
.
In cazul variatiei din fig.2.c, deoarece c2 este o functie monoton crescatoare cu a, rezulta ca miscarea este instabila pentru b<1/
6.2 Problema vascoasa
Studiul conditiilor in care o miscare isi poate pierde stabilitatea, respectiv determinarea unui numar Reynolds critic, se face numai cu considerarea efectului vascozitatii. Se considera o miscare de baza paralela plana, pentru care este valabila ecuatia completa Orr-Sommerfeld (136). Aceasta ecuatie fiind de gradul patru si liniara, pentru constructia solutiei generale este suficient sa cunoastem patru solutii liniar independente, notate f1 f2 f3 f4, iar solutia generala a ecuatiei (136) va fi:
![]() , (158)
, (158)
Conditia ca sistemul omogen (162) sa aiba solutii nenule este ca determinantul sistemului sa se anuleze:
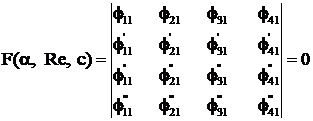 , (163)
, (163)
care reprezinta frontiera
de stabilitate, deoarece putem deduce din aceasta perechile de valori ![]() , Re pentru care ci = 0.
, Re pentru care ci = 0.
7 Instabilitatea termica
Mecanismul prin care se produce variatia densitatii este cel termic ca urmare a dilatarii unui fluid sub efectul incalzirii.
Instabilitatea termica apare in situatiile in care un lichid este incalzit in partea sa de jos. Cazul cel mai cercetat este un strat de lichid orizontal aflat pe o suprafata solida mai calda, cealalta suprafata de deasupra stratului de lichid, poate fi solida dar mai rece, sau poate fi o suprafata libera, in contact cu atmosfera, de asemenea mai rece. Efectul de tip Arhimede conduce la o forta verticala care modifica echilibrul static, invingand si efectele stabilizatoare ale vascozitatii si conductibilitatii termice [7, 16, 31, 49, 89, 109].
Rayleigh a formulat o teorie a instabilitatii convective a unui strat de lichid intre doua placi plane orizontale pentru fluide, denumite model Boussinesq, pentru care densitatea acestora variaza putin cu temperatura. Rayleigh a aratat ca instablitatea apare la depasirea unei valori critice a numarului Rayleigh (Ra):
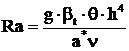 , (171)
, (171)
8 Ecuatiile generale pentru perturbatii
Se
analizeaza un fluid Boussinesq (densitate aproape constanta), aflat
in repaus care umple spatiul cuprins intre doua plane orizontale z =
0 si z = h, cu temperaturile T = ![]() si respectiv
si respectiv ![]() . Starea de baza a fluidului este caracterizata
prin:
. Starea de baza a fluidului este caracterizata
prin:
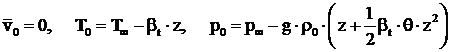 , (179)
, (179)
in domeniul ![]() , unde:
, unde:
![]() .
(180)
.
(180)
De mentionat ca variatia liniara a
temperaturii cu inaltimea z este o consecinta directa
a ecuatiei energiei (177), deoarece din ![]() , rezulta
, rezulta ![]() , iar instabilitatea apare numai daca
, iar instabilitatea apare numai daca ![]() .
.
Se considera ca peste starea de baza caracterizata prin relatiile (175), (176), (177), (179) apar perturbatii mici de forma:
![]() , (181)
, (181)
care vor satisface sistemul:
![]() , (182)
, (182)
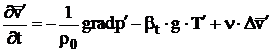 (183)
(183)
![]() (184)
(184)