Determinarea distantei focale prin metoda BESSEL

Determinarea distantei focale prin metoda BESSEL

1.   Scopul lucrarii:

Scopul acestei lucrari este prezentarea metodei Bessel si, implicit, determinarea distantei focale a unei lentile.

2.   Teoria lucrarii

Lentile optice subtiri

Descrierea lentilelor optice subtiri:

Prin lentila optica se intelege materialul transparent si omogen (de obicei sticla), separat de mediul exterior (de obicei aerul) prin doi dioptri (sferici sau combinatii de dioptri sferici si plani).

Sectiunile transversale tipice ale lentilelor folosite in practica, impreuna cu simbolizarea lor grafica in schemele optice, sunt indicate in figura 4.1, a, b.

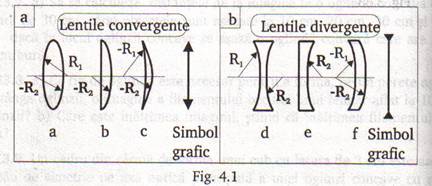
Lentilele din figura 4.1, a se numesc lentile convergente (positive), iar cele din figura 4.1, b poarta denumirea de lentile divergente (negative).

Din punct de vedere constructiv, lentilele convergente sunt mai groase in regiunea centrala, iar lentilele divergente sunt mai groase la margini.

Lentilele convergente pot fi biconvexe (a),  plan - convexe (b) si meniscuri convex - concave (c), iar lentilele divergente pot fi biconcave (d), plan - concave (e) si meniscuri concave - convexe (f).

Lentilele biconvexe cu razele de curbura egale se numesc echiconvexe, iar lentilele biconcave cu razele de curbura egale se numesc chiconcave.

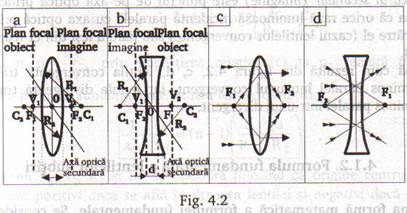
Elementele principale ale unei lentile sunt urmatoarele (fig4.2, a):

a)     Centrul optic, O, al lentilei

b)     Razele de curbura, R1 si R2, ale dioptrilor (potrivit conventiei de semen, R1>0 si R2<0, adica raza R1 este pozitiva, iar raza R2 este negativa).

c)     Centrele de curbura, C1 si C2, ale celor doi dioptri sferici.

d)     Axa optica principala, reprezentata de orice dreapta ce trece prin centrele de curbura C1 si C2. In cazul in care unul din dioptri este plan, axa optica principala este dreapta care trece prin centrul de curbura al dioptrului sferic si este perpendiculara pe dioptrul plan.

e)     Axa optica secundara, reprezentata de orice dreapta care trece prin centrul optic O, exceptand dreapta ce trece si prin centrele de curbura.

f)      Grosimea lentilei, d. Daca grosimea d (masurata pe axa optica principala) este neglijabila in raport cu razele de curbura R1 si R2 ale dioptrilor sferici, atunci lentila se numeste lentila subtire. In aceasta aproximatie se considera ca varfurile V1 si V2 ale dioptrilor se confunda cu centrul optic O al lentilei.

g)     Focarul primar (obiect) F1 si focarul secundar (imagine) F2 ale lentilei si distantele focale F1O, respective F2O. Planul care trece prin focarul F1 si este perpendicular pe axa optica principala se numeste plan focal - obiect, iar planul care trece prin focarul - imagine F2 se numeste plan focal - imagine.

La lentilele divergente (fig.4.2, b) focarele au semnificatii opuse cu focarele lentilei convergente, F2 fiind in stanga lentilei si F1 in dreapta ei.

Conform figurii 4.2, c,d:

focarul primar (obiect) este punctual de pe axa optica principala ce are proprietatea ca orice raza luminoasa care vine de la el (cazul lentilelor convergente) sau care se indreapta catre el (cazul lentilelor divergente) se deplaseaza, dupa refractie, parallel cu axa optica principala a lentilei.

focarul secundar (imagine) este punctual de pe axa optica principlala ce are proprietatea ca orice raza luminoasa incidenta paralela cu axa optica principala este refractata catre el (cazul lentilelor convergente) sau pare a iesi din el (cazul lentilelor divergente).

Dupa cum rezulta din figura4.2, c, d, lentila convergenta transforma un fascicul luminos paralel intr-unul convergent, iar lentila divergenta transforma un fascicul luminos parallel intr-unul divergent.

Formula fundamentala a lentilelor subtiri

Prima forma matematica a formulei fundamentale. Se considera o lentila subtire cu indicele de refractie n2 si se studiaza refractia in lentila ca doua refractii succesive pe doi dioptri sferici (fig.4.3).

Punctul - obiect A se afla in mediul cu indicele de refractie n₁, la distanta │x₁│ de lentila.

Primul dioptru (de raza +R₁) formeaza imaginea lui A in punctul A₁, ce apartine mediului cu indicele de refractie n₂ (al materialului lentilei) si se afla pe axa optica principala la distanta a de lentila. Pentru acest punct, A₁, relatia punctelor conjugate, cunoscuta de la studiul dioptrului sferic,   , se scrie: (a)

Pentru al doilea dioptru (de raza -R₂), punctul - obiect A₁ se afla in mediul cu indicele de refractie n₂ si imaginea sa, A₂ (identica cu imaginea finala data de lentila), se afla in mediul cu indicele de refractie  n₁, la distanta x₂ fata de lentila. Prin urmare, pentru al doilea dioptru, relatia punctelor conjugate se scrie: (b)

Adunanad relatiile (a) si (b) se obtine: sau

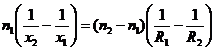
Intrucat , prin impartirea relatiei de mai sus la n₁ rezulta prima forma matematica a formulei fundamentale pentru lentile subtiri: 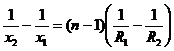(1)

Termenii x₁, x₂, R₁ si R₂ se masoara folosind ca origine centrul optic O al lentilei; ei sunt pozitivi daca se afla in dreapta lentilei si negativi daca se gasesc in stanga lentilei.

A doua forma matematica a formulei fundamentale. Din expresia (1) se obtin urmatoarele relatii pentru distantele focale:

- pentru x₁=∞:

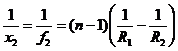  sau ;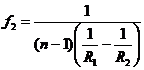

- pentru x₂=∞:

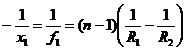  sau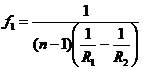

Notand: 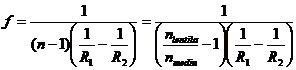(2)

se constata ca f = f₂ = -f₁, adica focarele sunt asezate simetric de o parte si de alta a lentilei. Relatia (2) se numeste ecuatia constructorului de lentile.

La lentilele divergente, asezarea focarelor si semnificatia lor sunt inverse decat in cazul lentilelor convergente. Prin urmare, la lentilele convergente, distanta focala este pozitiva (f>0), iar la lentilele divergente, distanta focala este negativa (f<0).

Cu aceste date se observa ca relatia (1) se mai poate scrie: (3)rezultand a doua forma matematica a formulei fundamentale pentru lentile subtiri, in care valorile numerice se vor introduce cu semnul minus pentru x₁ (daca obiectul luminos este situat in stanga lentilei) si pentru distanta focala f a lentilei divergente, respectiv cu distanta focala f pozitiva la lentilele convergente.

Din relatia (3) se deduc formulele necesare rezolvarii problemelor:

, , (4)

Imaginea va fi reala daca x₁ si x₂ au semne contrare, respectiv virtuala daca x₁ si x₂ au acelasi semn.

Examinand relatia (2) se constata ca proprietatea unei lentile de a fi convergenta sau divergenta depinde de:

forma geometrica (prin razele de curbura, R₁, R₂)

natura materialului (prin indicele de refractie al lentilei, n_lentila)

mediul in care este plasata (prin indicele de refractie al mediului n_mediu)

Altfel spus, aceeasi lentila poate fi convergenta daca se afla intr-un mediu in care sau poate fi divergenta intr-un alt mediu in care .

Distanta focala va fi : .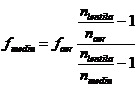

3.   Materiale experimentale necesare

bara metalica pe care se fixeaza aparatele

lentila, lumanare, ecran - prevazute cu cleste pentru fixare pe bara

linie gradata milimetric

4.   Modul de lucru

Se aseaza pe stativ lumanarea, lentila si ecranul astfel incat lentila sa fie intre lumanare si ecran. Distanta dintre lumanare si ecran (L) ramane constanta iar lentila este mutata de-a lungul barei pana se poate observa pe ecran o imagine clara a obiectului. Se muta lentila succesiv si se inregistreaza valorile (d). Apoi distanta L se modifica si se repeta mutarile succesive ale lentilei pentru obtinerea imaginii clare pe ecran.

5.   Culegerea datelor experimentale

=

1. mm

2. mm

3. = mm (eliminam valoarea de 673mm deoarece este mult diferita de celelalte valori inregistrate)

4. = mm

5. = mm  (eliminam valoarea de 649mm deoarece este mult diferita de celelalte valori inregistrate)

6.   Prelucrarea datelor

f =

1. f = mm

2. f = mm

3. f = mm

4. f = mm

5. f = mm

=

= mm

ε = │ - f_n│

1. ε = │54,079 - 54,027│= 0,052 mm

2. ε = │54,079 - 54,262│= 0,183 mm

3. ε = │54,079 - 54,115│= 0,036 mm

4. ε = │54,079 - 54,161│= 0,082 mm

5. ε = │54,079 - 53,831│= 0,248 mm

ε = mm

Deci valoarea f = ± ε = 54,079 ± 0,1202

7.   Surse de erori

Erorile ce survin in timpul experimentului determina valori fluctuante. Ele pot fi datorate ustensilelor folosite sau pot fi erori umane. Forma pe ecran a unei imagini aparent clara, dar care, in urma unor miscari ulterioare ale lentilei, ar putea deveni mult mai precisa este o eroare evidenta datorata atat aparatelor de laborator cat si capacitatii reduse de distingere a informatiilor luminoase de catre ochiul uman.

Lumina lumanarii are o calitate redusa variind ca intensitate si raspandind razele luminoase sferic, spre deosebire de un laser, spre exemplu, care are fascicul luminos focalizat intr-un punct. O alta sursa de erori poate fi calitatea ecranului deoarece poate avea suprafata denivelata sau inchisa la culoare, ceea ce duce la reflexii difuze si la absorbtia razelor de lumina. Calitatea redusa a lentilei poate fi o sursa de eroare datorita depunerii particulelor de praf care conduc la o oarecare opacifiere a instrumentului optic impiedicand razele de lumina si dand senzatia unei imagini neclare. In timpul masuratorii, fixarea neprecisa a dispozitivelor pe bara metalica poate duce la alunecarea acestora si la modificari majore ale datelor experimentale.

Erori umane majore, pe langa calcule inexacte apar si in cazul masuratorilor cu rigla, fractiuni de milimetri, care nu pot fi inregistrate de ochiul uman, conduc la erori. Pentru distingerea clara a imaginii a fost necesara stingerea luminii in laborator, dar ochiul uman are nevoie de 30 de minute pentru a se acomoda si pentru a putea percepe corect semnalul luminos in intuneric, iar executantul experimentului nu a avut la dispozitie acest interval de timp si de aceea distingerea imaginii a fost relativ inexacta. Unii executanti pot avea probleme de vedere (miopie, hipermetropie) ce necesita corectare prin lentile biconvexe sau biconcave, ceea ce duce la erori deoarece lumina ajunge pe retina dupa ce trece prin acest nou dioptru suferind reflexii si absorbtii si implicit se creaza senzatia unei imagini neclare.

Caracterul complex al luminii si existenta undelor electro-magnetice conduc la intensitati diferite si, implicit, la fluctuatie claritatii imaginii. Faptul ca optica geometrica opereaza cu numeroase conventii si conditii ideale conduce la erori.

8.   Metode de imbunatatire

Sunt greu de gasit mijloace de remediere a acestor erori, fiind vorba de surse de erori datorate limitelor umane de perceptie sau de calcul sau ustensilelor de laborator care ar trebui inlocuite cu unele mult mai performante, caz in care este nevoie de substantiale resurse financiare. O metoda de remediere a erorilor este imbunatatirea lentilei prin fabricarea ei din sticla organica (stiplex), material cu o transparenta sporita. Ecranul trebuie sa fie complet alb, cu o putere mare de reflexie. Sursa de lumina difuza si variata pe care o reprezinta lumanarea trebuie inlocuita cu una de tip laser, cu fascicul luminos focalizat. Este necesar, de asemenea, un computer, atat pentru calcule, cat si pentru masuratori. Trebuie mentinuta o intensitate constanta a sursei de lumina si perfectionata masurarea conturului imagini (care sa tinda la un minim). Experimentul trebuie realizat intr-o incapere complet izolata, eventual in vid, iar indicarea valorilor trebuie realizata prin marcaj electronic.

Distanta focala a lentilei ar putea fi masurata si prin alte modalitati alternative, de o mai mare precizie, care sa opereze la nivel molecular al lentilei supusa unor anumite conditii de temperatura si presiune, utilizand spectre in infrarosu si RMN sau substante chimice optic active.