Cercetari in domeniul arderii difuzive a combustibililor gazosi

CERCETARI IN DOMENIUL ARDERII DIFUZIVE A COMBUSTIBILILOR GAZOSI

Pe plan mondial se face puternic simtita ascensiunea turbinelor cu gaze, ca urmare a dezvoltarii tehnologiei de obtinere a unor materiale rezistente la temperaturi inalte, a unor arzatoare perfectionate cu productie redusa de noxe si a sistemelor de racire eficienta a pieselor aflate in zona temperaturilor inalte. Exista o preocupare majora de informare si corelare a cercetarilor europene in cadrul unor programe internationale de tip FP V si FP VI la care a aderat si Romania, prin care se doreste implementarea acestor sisteme moderne de producere a energiei electrice si termice cu un grad ridicat de eficienta si in conditii de maxima protectie a mediului [4, 20, 35, 65, 70, 114].

1.1.1 Ecuatiile fundamentale pentru substantele simple

Pentru substantele individuale aflate intr-o anumita faza, caldurile molare izobare se aproximeaza in functie de temperatura prin expresii polinomiale de forma [4, 20, 35, 65, 70, 114]:

, (1.1)

sau prin combinatii liniare ale unor functii cu :

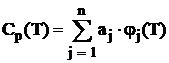, (1.2)

Utilizand derivatele entalpiei H si ale entropiei S in raport cu temperatura la presiune constanta:

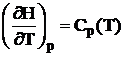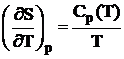; , (1.3)

Notand temperatura cu T si inlocuind relatiile (1.12) si (1.13) in (1.6) si (1.7) obtinem:

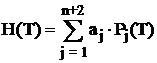, (1.18)

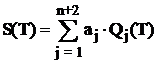. (1.19)

1.1.2 Echilibrul chimic

Echilibrul chimic pentru amestecuri de gaze care reactioneaza se defineste in termodinamica chimica pe baza principiului al doilea al termodinamicii, cu ajutorul potentialelor chimice.

Principiul al doilea al termodinamicii se poate exprima sub forma

TdS  dH - Vdp,

de unde rezulta, pentru un sistem in care au loc procese la presiune si temperatura constanta:

dG_p,T  0, (1.25)

unde: G = H - TS este entalpia libera, sau energia libera Gibbs. Prin urmare, pot avea loc numai procesele insotite de scaderea energiei libere Gibbs; cand energia libera Gibbs atinge valoarea minima, care se mentine in continuare constanta, sistemul se afla la echilibru chimic.

Pentru un amestec de j substante, fiecare in cantitatile v_i moli, diferentiala totala dG este in general

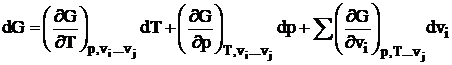, (1.26)

unde:

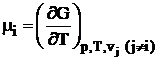- potentiale chimice ale componentilor i.

1.1.3 Suprafata de reactie

Ecuatia suprafetei de reactie in flacara difuiziva pentru procesul adiabatic se poate obtine prin rezolvarea ecuatiei [4, 20, 35, 65, 70, 114]:

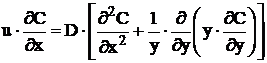(1.39)

in care 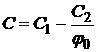,-sunt concentratii, iar reprezinta cantitatea de moli de oxigen care reactioneaza cu un mol de gaze combustibile,cu urmatoarele conditii la limita:

pentru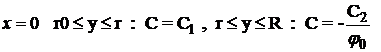

si 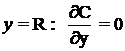(1.40)

Integrarea ecuatiei (1.39) permite determinarea interdependentei dintre concentratiile si in tot spatiul flacarii. Din conservarea entalpiei totale in orice punct al spatiului flacarii se obtine relatia:

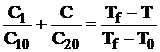, (1.41)

In cazul camerei de ardere cilindrice, miscare axial simetrica, din (1.45) cu conditiile (1.40), se obtine solutia:

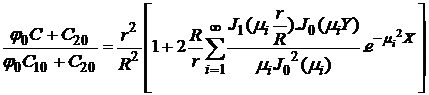, (1.46)

in care reprezinta radacinile ecuatiei , iar si sunt functiile Bessel de ordinul zero si unu.

1.3.1 Calculul parametrilor de stare in vecinatatea punctului Chapman- Jouguet superior (CJs)

In fig. 1.3 se reprezinta variatia presiunii si entropiei, in vecinatatea punctului Chapman-Jouguet superior:

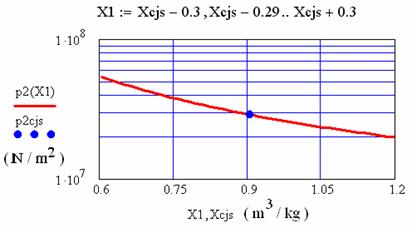
Fig. 1.3 Variatia presiunii in vecinatatea punctului Chapman-Jouguet superior

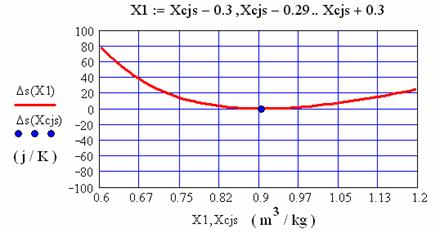
Fig. 1.4 Variatia entropiei in vecinatatea punctului Chapman-Jouguet superior

1.4 Difuzia moleculara unidimensionala nestationara in gaze

Difuzia pura sau moleculara se caracterizeaza prin diminuarea gradientilor de concentratie existenti in limitele unei faze oarecare si se produce prin migrarea atomilor sau moleculelor in lipsa curentilor de convectie.

Difuzia in regim stationar are loc in cazul in care intre doua puncte se mentine o diferenta constanta de concentratie, fenomenul fiind descris de prima lege a lui Fick [4, 20, 35, 65, 70, 114]:

[kmoli/m²s] , (1.51)

unde J este fluxul de difuzie (J = const.), D [m²/s] - coeficientul de difuzie, C - concentratia substantei care difuzeaza (molecule/m), - gradientul de concentratie.

Difuzia in regim nestationar se caracterizeaza prin variatia in timp a fluxului de difuzie si este descrisa de legea a doua a lui Fick

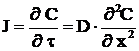. (1.52)

Pe baza teoriei cinetice a gazelor se deduce relatia :

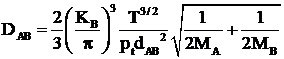[m/s²] , (1.53)

unde D_AB este coeficientul de difuzie a gazelor A si B care difuzeaza , K_B este constanta lui Boltzmann (K_B = 1,38 10 ^{- 9}) [J/molec*K], d_AB - diametrul mediu al moleculelor (d_AB = (d_A + d_B) / 2    [m]) , M_A,M_B - mase moleculare [Kg/mol] , p_t - presiunea totala [N/m²], T - temperatura [K] .

1.5 Stabilizatori de flacara

1.5.1 Scheme de tip Helmholtz

Metoda hodografica a lui S.A.Ciaplighin este aplicabila la problemele de tip Helmholtz si Kirchoff, probleme care pun in evidenta o marime specifica miscarilor care se studiaza si anume viteza caracteristica. Aceasta marime se considera a fi viteza de pe liniile libere, care are o valoare constanta, conform teoriei miscarilor cu linii de discontinuitate, pentru viteze. Teoria de mai sus a fost imaginata, pentru a se indeparta paradoxul lui D'Alembert, care consta in afirmarea lipsei de rezistenta la inaintare a unui corp care se misca intr-un fluid.

Teoria lui Helmholtz, reluata si de Kirchhoff, conduce la valori prea mici pentru rezistenta ce o incearca un solid in miscarea sa prin mediul fluid; acest lucru nu este surprinzator deoarece teoria aceasta neglijeaza complet efectele turbionare care se produc in spatele obstacolului, pe care singura vascozitatea le poate explica si admite doar existenta unei zone in care fluidul este antrenat cu obstacolul.

Teoria lui Helmholtz a fost dezvoltata prin metoda lui Levi-Civita care exprima solutia nedefinita a problemei ca o functionala de una sau mai multe functii q(s), intim legate de forma obstacolului si a peretilor solizi, dar a carei determinare cere rezolvarea unor ecuatii functionale neliniare. A doua problema pe care o pune teoria lui Helmholtz, anume, determinarea miscarii care corespunde unor pereti dati si nu construiti, dupa ce s-au dat functiile q(s), peretii fiind definiti prin ecuatia lor intrinseca, cere rezolvarea ecuatiilor functionale amintite. Astfel ipoteza lui Helmholtz revine la a neglija fenomenele turbionare foarte complicate care se intampla in aceasta regiune si a considera acolo fluidul in repaus, deci legat de obstacol (fig. 1.10)

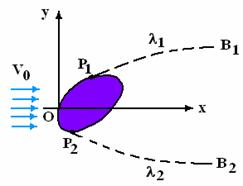
Fig. 1.10 Modelul lui Helmholtz

Se formeaza astfel in spatele obstacolului o regiune cu fluid imobil, pe care experienta o confirma pentru numerele lui Reynoltz foarte mari, iar traiectoriile particulelor fluide () detasate de pe frontiera obstacolului nu se vor mai intalni in spatele acestuia, ci se vor intinde la infinit aval, cu directii asimptotice paralele cu directia vitezei a fluidului, la infinit amonte (directia generala de miscare a curentului).

1.5.4 Modelul Cheng - Kovity

Modelul Cheng si Kovitz, pentru stabilizarea flacarii la spatele obstacolului, este aratat in fig. 1.18.

Vartejul de gaze calde, recirculate la spatele obstacolului, se compune din doi curenti: unul de acelasi sens cu curentul principal in contact cu acest curent, celalalt curgand in sens contrar in apropierea axei sistemului, cu cei doi curenti mentionati [4, 20, 35, 65, 70, 114].

Pentru efectuarea calculelor se presupune ca flacara laminara este ancorata in punctul P la distanta x_i de marginea A a obstacolului. Pentru ca in punctul P sa poata sa ia nastere si sa se mentina un front de flacara, este necesar ca aportul de caldura preluata de la frontul de flacara de gazele vartejului pe distanta PS, la care se adauga caldura degajata prin reactiile de ardere din interiorul vartejului, sa fie suficienta sa compenseze pierderile de caldura spre exterior si caldura transmisa pentru aprinderea amestecului combustibil proaspat pe distanta AP.

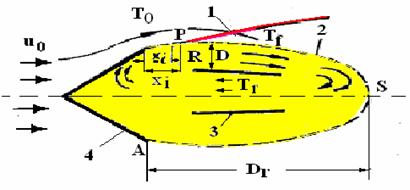
Fig. 1.18 Modelul Cheng si Kovitz pentru calculul distantei

de acrosare a fla­carii x_i , la spatele obsta­colului:

1 - frontul de flacara; 2 - linie de separatie intre zona de curgere

si de recirculatie; 3 - linie de stagnare; 4 - obstacol V.

Din ecuatia de bilant de caldura bazata pe ipotezele de mai sus rezul­ta, relatia:

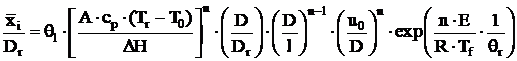(1.89)

in care: exponentul n = 3/2 4/3; este distanta medie de la marginea obstacolului A (fig.1.18) pana la centrul de aprindere P; D_r - lungimea arcului AS; - constanta adimensionala; c_p - caldura specifica la presiune constanta a amestecului combustibil proaspat; T_f, T_r, T₀ - tempe­ratura zonei flacarii, zonei de recirculatie si amestecului combustibil proaspat: - caldura de ardere, in J g^-1; E - energia de acti­vare, in J ∙ mol^-1; R - constanta universala a gazelor; A - factorul de frecventa in expresia vitezei de reactie; - viteza curentului in amonte de obstacol, in cm ∙ s^-1; D - distanta intre linia de separatie 2 si linia de stagnare 3 (fig. 1.18), in cm; l - lungimea efectiva (cm) a placii plate a obstacolului care defineste conditiile de frecare inainte de zona de stagnare din spatele obstacolului).

1.6 Determinarea vitezei de rupere a flacarii turbulente de difuziune

Daca se noteaza cu viteza curentului pe axa jetului, conditia de stabilitate a flacarii este:

.                         (1.91)

Daca se considera pentru expresia data de Williams si Bollinger,

,                 (1.92)

valabila pentru Re = 3 00080000), in care: este viteza maxima a scarii laminare, in cm s^-1; d ₀ - diametrul gurii arzatorului, in cm, iar pentru u_m expresia data de Abramovici.

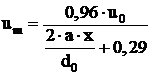, (1.93)

in care: este viteza curentului in gura arzatorului; x - distanta de la gura arzatorului pana la sectiunea de calcul a jetului (fig.8.38), si daca se inlocuiesc in ecuatia (8.28) rezulta: 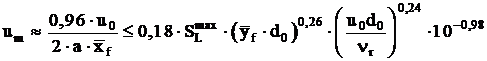(1.94)

unde: , este lungimea raportata a flacarii pana la sectiunea la care se realizeaza egalitatea C_m = C_s , adica concentratia de combustibil gazos pe axa jetului este egala cu concentratia stoichiometrica a amestecului com­bustibil, ( depinde numai de natura combustibilului gazos); - diametrul raportat al zonei de amestecare a jetului in sectiunea transversala in care concentratia pe axa jetului C_m = C_s ( depinde numai de natura combustibilului gazos); n_s - vascozitatea cinematica a amestecului combustibil - aer la ruperea flacarii, in ; a - coeficientul de structura al jetului (a 0,07) ; d₀ - diametrul, in mm; , in m s^-1.

1.7 Determinarea lungimii de desprindere a flacarii turbulente de difuziune

Pentru a calcula variatia concentratiei C in lungul jetului, poate   fi adoptata o relatie de forma:

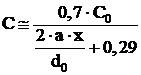, (1.102)

in care C₀ este concentratia de combustibil gazos in gura arzatorului.

Pentru M_a = M_g, rezulta:

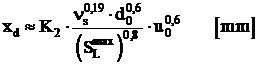, (1.104)

iar pentru cazul , rezulta:

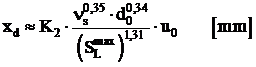, (1.105)

unde d₀ este dat in mm.