Densitatea sarcinii electrice

Densitatea sarcinii electrice

Sarcina electrica q este o marime globala, care descrie starea de electrizare la nivelul intregului corp. Se constata, experimental, ca -in general- sarcina electrica nu se repartizeaza uniform, in toate punctele unui corp. In unele cazuri, la nivel global, sarcina electrica a unui corp poate fi nula, corpul fiind considerat -in ansamblul sau- ca fiind neutru din punctul de vedere al electrizarii. Chiar si in aceasta situatie, in unele punctele -din interiorul corpului sau dupa suprafata lui- se poate ca starea locala de electrizare sa fie diferita de zero.

De aceea, s-au introdus doua marimi derivate care sa descrie local (in fiecare punct al corpului) starea de electrizare. Acestea sunt: densitatea de volum a sarcinii electrice si densitatea de suprafata a sarcinii electrice, care sunt functii scalare de punct, pozitive sau negative.

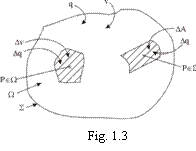Densitatea de volum a sarcinii electrice. Considerand un corp oarecare electrizat (asa ca cel reprezentat in figura  1.3) care ocupa domeniul Ω si are sarcina electrica globala q (pentru intregul corp , unde este suprafata ce delimiteaza corpul Ω), potrivit principiului localizarii starilor si actiunilor din Fizica, sarcina electrica q (care este o marime aditiva) se poate extinde oricum in si pe corpul , deci si pe portiuni finite oricat de mici in interiorul crpului sau/si pe suprafata lui ΔA, cu valori Δq care sunt fractiuni ale sarcinii globale q (fig. 1.3). In aceste conditii pentru orice punct din interiorul corpului (PIW) se poate defini o marime derivata care sa descrie cum se repartizeaza local, in interiorul corpului, sarcina electrica; aceasta marime se noteaza cu q_v (traditional cu r) si se defineste astfel:

(1.4)                   ,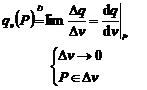

care, mai general, se mai poate scrie si sub forma sau . In expresia din definitia (1.4), densitatea de volum a sarcinii electrice q_v(P) apare ca o functie scalara de punct, calculata prin limita raportului dintre o "fractiune" de sarcina, din q, ce se afla in portiunea de volum si care contine punctul P in care se determina densitatea de volum a sarcinii electrice, astfel ca atunci cand punctul P este mentinut in permanenta in interiorul lui .

Asa cum este definita prin expresia (1.4), q_v(P) sau , constituie un camp scalar, pozitiv si/sau negativ, si anume acela al densitatii de volum a sarcinii electrice. Daca se spune ca volumul corpului este uniform electrizat .

Unitatea de masura a densitati de volum a sarcini electrice este coulombul pe metru la cub, cu simbolul C/m.

Ecuatia dimensionala a densitati de volum a sarcinii electrice este: [q] = [Q][L].

Densitatea de suprafata a sarcinii electrice. Considerandu-se tot figura 1.3 si principiile aratate in aliniatul anterior, se defineste si marimea de punct ce descrie  starea locala de electrizare a suprafetei unui corp, denumita densitate de suprafata a sarcini electrice, care se noteaza cu qsau (traditional cu ), si se defineste prin:

, (1.5)

care, mai general, se poate scrie si sub forma sau. In definitia (1.5), P este orice punct de pe suprafata , in jurul caruia se ia o portiune de suprafata ce contine puntul P considerat si are o sarcina electrica , ca fractiune a sarcinii electrice globale q a intregului corp . Limita din expresia (1.5), adica , se ia astfel incat in permanenta punctul P sa fie in interiorul lui , oricat de mica ar deveni.

Marimea derivata "densitatea de suprafata a sarcinii electrice" are valori scalare , negative sau pozitive, ce se exprima prin unitatea de masura coulomb pe metru  la patrat

Ecuatia dimensionala a densitati de suprafata a sarcini electrice este:

Sarcina electrica globala q a unui corp se poate calcula in functie de distributiile pe cu expresia evidenta (rezultata din definitiile 1.4 si 1.5):

. (1.6)