APLICAREA METODELOR NUMERICE IN STUDIUL ARDERII DIFUZIVE A COMBUSIBILILOR GAZOSI

1 Metoda modelarii fractiei de amestec/PDF (Probability Density Functions)

Metoda modelarii fractiei de amestec / PDF a fost dezvoltata pentru simularea flacarilor difuziv turbulente si a proceselor de reactie similare in care turbulenta furnizeaza o limitare a vitezei reactiei chimice. Pentru astfel de sisteme, metoda PDF ofera multe beneficii in raport cu formularea vitezei finite. Metoda fractiei de amestec permite modelarea formarii compusilor chimici intermediari, a efectelor disocierii, si permite luarea in considerare intr-un mod riguros a cuplajului dintre turbulenta si reactia chimica [5, 14, 35, 44, 67, 121].

Mecanismele de reactie, care pot fi necunoscute sau extrem de complexe, nu sunt definite explicit, in locul acestora, in sistemul reactant se utilizeaza:

reactia chimica infinit de rapida (stratul de flacara, sau conceptul “amestecat ars”);

calcule de echilibru chimic;

calcule de neechilibru (fasiile de flacara).

Metoda modelarii fractiei amestecului se bazeaza pe un set de ipoteze simplificatoare, iar starea termo - chimica instantanee a fluidului este raportata la o cantitate scalara ce se conserva in timpul procesului chimic, denumita fractia amestecului, . Pentru un sistem binar, constand din combustibil si oxidant, fractia amestecului poate fi scrisa in termenii participatiei masice elementare sub forma:

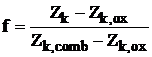(1)

unde este participatia masica elementara pentru un element k . Indicele inferior “ox” indica valoarea participatiei masice a elementului “ k ” la intrarea curentului de oxidant in domeniul de analiza, iar indicele inferior “comb”, indica valoarea participatiei masice a elementului “ k ”, la intrare in domeniul de analiza a curentului de combustibil. Pentru sisteme complexe combustibil-oxidant, fractia amestecului poate fi definita mai simplu ca participatie masica locala a combustibilului, unde prin “combustibil” se intelege intreg amestecul de substante ce joaca rol de combustibil pentru reactia de ardere in problema analizata. Astfel, in cazul in care curentul de combustibil contine CH₄ si CO, “participatia masica locala a combustibilului” este reprezentata de participatia masica a amestecului de combustibili (CH₄ si CO) si nu doar de participatia masica a CH₄. Daca curentul secundar (reprezentand un alt combustibil, alt oxidant sau un fluid nonreactant) este inclus in calcule, combustibilul si fractiile de amestec secundar sunt reprezentate de participatiile masice ale combustibilului si ale curentilor secundari. Suma tuturor celor trei fractii de amestec din sistem (combustibilul, curentul secundar si oxidantul) este totdeauna egala cu unitatea:

(2)

Aceasta indica, conform figurii 2 a, ca doar punctele din planul ABC in spatiul fractiei amestecului sunt valabile. In consecinta, cele doua fractii ale amestecului, si , nu pot varia independent: valorile lor sunt corecte doar daca ele vor fi situate in acelasi timp in interiorul triunghiului OBC din figura 2. b.

Fig. 2 Relatia dintre , si

1.4 Modele pentru abordarea echilibrului chimic in arderile

nepreamestecate

Abordarea pentru o singura fractie de amestec

Pentru a mentine timpul de calcul la minimum, majoritatea calculelor necesare pentru modelul arderii nepreamestecate, sunt realizate in afara Fluentului, prin procesarea calculelor chimiei si a integrarii PDF intr-un cod separat, numit prePDF. In figura 9 este ilustrat cum este impartit calculul intre preprocesor (prePDF) si rezolvitor (FLUENT). In prePDF, modelul chimiei (amestecat este ars, echilibrul chimic sau flacari laminare) este folosit impreuna cu forma asumata a PDF, pentru a realiza integrarea ecuatiilor (15), (17), si/sau (24). Aceste integrale sunt calculate cu prePDF si memorate in tabele care descriu variatia valorilor medii termochimice (temperatura, densitatea si fractiile masice ale speciilor) in functie de valorile , si .

De notat ca varianta fractiei de amestec este folosita pentru obtinerea de date sub forma de tabele, unde

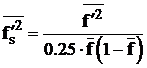                           (28)

Date sub forma de tabele pentru sisteme adiabate

Conceptul de tabela generata de prePDF,se refera la un sistem cu o singura fractie de amestec. Ea furnizeaza Fluent-ului valorile pentru si intr-un punct din domeniul de curgere, valorile mediate in timp ale fractiilor masice, densitatii si temperaturii (). Fluent foloseste ecuatia (28) pentru a calcula varianta medie a fractiei de amestec intrucat tabela fractiei de amestec contine datele corespunzatoare .

Tabela este rezultatul matematic al integrarii ecuatiei (17). Se calculeaza o tabela pentru fiecare scalar (fractia masica a speciilor, densitatea, temperatura). In sistemele adiabatice, unde entalpia instantanee este functie doar de fractia de amestec instantanee, se determina o tabela cu doua dimensiuni.

Fig. 9 Modul de calcul al programului FLUENT si prePDF

pentru o fractie de amestec

Pentru un sistem cu doua fractii de amestec, se vor determina valorile instantanee ale temperaturii, densitatii si a fractiilor masice ale speciilor (ecuatiile 10 sau 13) si se vor memora in tabelele corespunzatoare. Pentru cazul sistemului adiabatic cu doua fractii de amestec tabelele cuprind , si ca functie de fractia de amestec a combustibilului si de fractia secundara partiala (fig. 10).

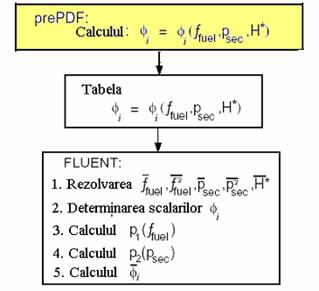
Fig. 10 Modul de calcul al programului FLUENT si prePDF

pentru doua fractii de amestec

2 Modelare numerica cu metoda volumului finit

2.1 Arhitectura configuratiei analizate

Se considera cazul a trei duze cu axele in acelasi plan (fig. 11). Diametrul duzelor este de 5 mm iar distanta dintre axe este de 10 cm. Prin duze curge gaz cu viteza de 20 m/s. Duzele sunt pozitionate in curent de aer cu viteza de 1 m/s. Distributia vitezelor pe sectiunile de intrare a gazului si a aerului se considera constanta.

Pentru studiul curgerii se considera un domeniu cilindric cu baza eliptica, cu dimensiunile prezentate in figura 12.

Fig. 11 Domeniu cilindric Fig. 12 Geometria domeniului cilindric

2.2 Discretizarea domeniului si tabelele fractiilor de amestec

Domeniul s-a discretizat cu elemente tetraedrale. In figura 13 se prezinta fetele celulelor pe planele de simetrie si pe sectiunile de intrare.

Fig. 13 Discretizarea domeniului (fetele elementelor pe planele de simetrie,

pe intrarile in domeniu si pe pereti)

Tabelele calculate pentru temperatura, densitate, fractii molare ale speciilor sunt prezentate in figurile 14-20.

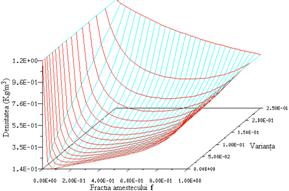
Fig. 14 Tabela PDF - temperatura. Fig. 15 Tabela PDF - densitatea.

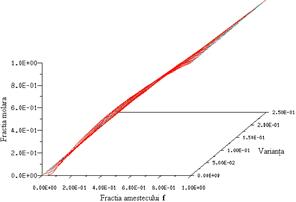
Fig. 16 Tabela PDF - fractia molara CH₄ Fig. 17 Tabela PDF - fractia molara O₂

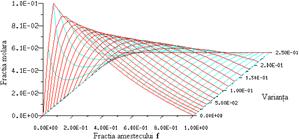
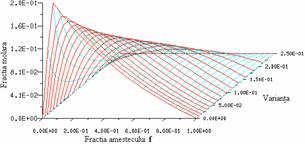
Fig. 18   Tabela PDF - fractia molara CO₂ Fig. 19 Tabela PDF - fractia molara H₂O

2.3 Rezultate obtinute prin modelare cu metoda volumului finit

In urma calculelor numerice, a rezultat o variatie a campului vitezelor pe cele doua plane de simetrie, prezentate in figura 21 si 22 si o variatie a campului temperaturilor prezentate in figura 23 si 24.

In figurile 25 – 32 sunt prezentate campurile de fractii masice ale speciilor , , si , pe cele doua plane de simetrie ale domeniului.

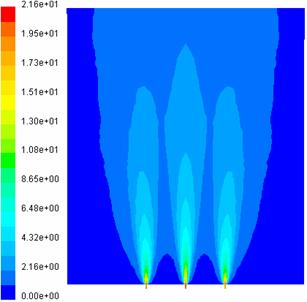
Fig. 21 Campul de Fig. 22 Campul de

viteze pe planul de simetrie 1 viteze pe planul de simetrie 2

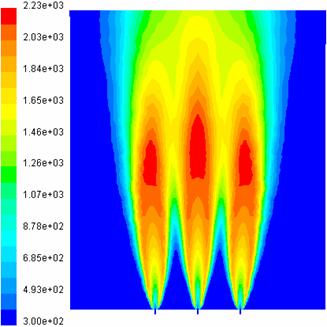
Fig. 23 Campul de temperaturi Fig. 24 Campul de temperaturi

pe planul de simetrie 1 pe planul de simetrie 2

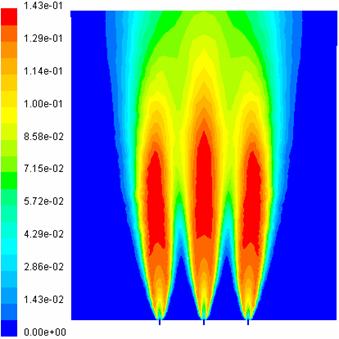
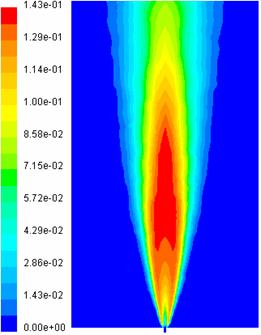
Fig. 27 Campul de fractii masice Fig. 28 Campul de fractii masice

de CO₂ pe planul de simetrie 1 de CO₂ pe planul de simetrie 2

2.4 Grafice ale variatiei vitezelor si temperaturilor

In figura 33 sunt prezentate variatiile vitezei dupa axa duzei centrale (cu negru) si dupa axa unei duze laterale (cu rosu). Considerand trei directii orizontale aflate in planul axelor celor trei duze, in figura 34 sunt prezentate variatiile vitezei dupa cele trei directii. Ordonata este masurata din dreptul axei duzei centrale.

Fig. 33 Variatia vitezelor dupa Fig. 35 Variatia temperaturilor

axele duzei centrale si lateraledupa axele duzei centrale si laterale