
|
|
|
Scopul lucrarii: prezentarea schemei bloc, a terminologiei si a criteriilor de stabilitate specifice circuitelor cu reactie, exemplificarea acestora folosind scheme de oscilatoare elementare.
Prezentarea lucrarii
Un sistem cu reactie (feedback) se caracterizeaza prin faptul ca legatura intrare-iesire este bidirectionala: semnalul de la intrare circula spre iesire parcurgand o asa-numita cale directa, iar semnalul de la iesire este recirculat spre intrare parcurgand o cale inversa, denumita cale de reactie. Schema-bloc a unui astfel de circuit se prezinta in Fig.1:
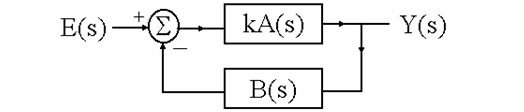
1 Figura 1
Blocul notat cu kA(s) se numeste amplificator pe calea directa, iar cel notat cu B(s) se numeste amplificator pe calea de reactie. Reactia se considera negativa daca semnalul recirculat de la iesirea circuitului spre intrare tinde sa micsoreze semnalul total aplicat intrarii amplificatorului de baza, (k>0). In caz contrar, reactia se considera pozitiva (k<0).
Functia de transfer a circuitului, denumita functie de transfer in bucla inchisa, se calculeaza cu formula de mai jos (considerand reactia negativa):
![]()
1
Marimea kA(s)B(s) se numeste functie de transfer in bucla deschisa a circuitului cu reactie.
Studiul stabilitatii unui circuit cu reactie se poate efectua utilizand criteriul general de stabilitate a unui circuit liniar, criteriul Routh-Hurwitz. Totusi, tinand cont de forma particulara a functiei de transfer a circuitului s-au elaborat si criterii specifice, care folosesc urmatorul principiu: studiind functia de transfer in bucla deschisa a circuitului se trag concluzii privind stabilitatea circuitului in bucla inchisa. Este un principiu extrem de util in practica, deoarece in cazul unui sistem cu reactie instabil, inchiderea buclei poate deveni periculoasa, putand conduce la distrugerea circuitului.
Dintre criteriile de stabilitate specifice circuitelor cu reactie mentionam:
- Criteriul Nyquist: Un sistem cu reactie este stabil daca hodograful functiei de transfer in bucla deschisa inconjoara punctul (-1,0) de P ori in sens trigonometric (sens invers acelor de ceasornic).
Exista cateva marimi de interes care se definesc in contextul utilizarii acestui criteriu:
Z: numarul de zerouri din semiplanul drept ale functiei 1+kA(s)B(s) (care reprezinta, in acelasi timp, poli ai functiei de transfer in bucla inchisa);
P: numarul de poli din semiplanul drept ai functiei de transfer in bucla deschisa kA(s)B(s);
N: numarul de inconjururi pe care le efectueaza hodograful functiei de transfer in bucla deschisa in jurul punctului (-1,0). N se considera pozitiv daca inconjurul se efectueaza in sens orar si negativ daca se efectueaza in sens trigonometric.
Criteriul Nyquist presupune utilizarea formulei Z=N+P si pentru ca sistemul in bucla inchisa sa fie stabil este necesar ca Z=0.
Dupa cum stim, hodograful unei functii complexe se traseaza intr-un sistem de coordonate reprezentat de partea sa reala, respectiv partea sa imaginara. Semnificatia unui punct de pe hodograf este urmatoarea: daca unim originea cu punctul respectiv, lungimea vectorului este egala cu modulul functiei de transfer in bucla deschisa, iar unghiul format de vectorul respectiv cu axa absciselor este egal cu argumentul functiei de transfer in bucla deschisa in dreptul unei anumite frecvente.
- Locul radacinilor: Un sistem cu reactie este stabil daca locul geometric descris de solutiile ecuatiei: 1+kA(s)B(s)=0 pentru diverse valori ale lui k (grafic care este denumit locul radacinilor) nu are portiuni cuprinse in semiplanul drept.
Acest grafic se traseaza aplicand un set de reguli foarte simple, dintre care enumeram:
- locul radacinilor pleaca din polii si se termina in zerourile functiei de transfer in bucla deschisa;
- portiunile din locul radacinilor aflate pe axa absciselor se gasesc la stanga unui numar impar se singularitati (poli sau zerouri);
- portiunile din locul radacinilor aflate pe axa absciselor si cuprinse intre 2 singularitati de acelasi fel se desprind de pe axa sub un unghi de 90
- ramurile spre care portiuni din locul radacinilor tind asimptotic formeaza cu axa absciselor unghiuri care se calculeaza cu relatia:
![]()
2
in care P si Z reprezinta numarul de poli, respectiv de zerouri finite ale functiei de transfer in bucla deschisa.
Observatie: P si Z au alta semnificatie decat la criteriul Nyquist!
- asimptotele se intersecteaza intr-un punct plasat intotdeauna pe axa reala, denumit centru de greutate, a carui abscisa se calculeaza cu formula:
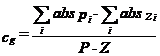
3
Semnificatia unui punct de pe locul radacinilor este urmatoarea: coordonatele acestuia reprezinta valoarea (reala sau complexa) a unei solutii a ecuatiei 1+kA(s)B(s)=0 pentru o valoare particulara a parametrului k. Acesta este motivul pentru care se spune ca locul radacinilor este gradat in valori ale lui k (in sensul ca in loc sa precizam coordonatele in planul complex ale unui punct de pe grafic putem indica valoarea lui k pentru care punctul respectiv este solutie a ecuatiei mai sus mentionate).
- Criteriul Barkhausen: Un sistem cu reactie este stabil in bucla inchisa daca modulul functiei de transfer in bucla deschisa este subunitar in dreptul frecventei la care faza acesteia este 180
Se definesc urmatoarele marimi:
- rezerva de amplitudine: diferenta dintre 1 si modulul functiei de transfer in bucla deschisa in dreptul frecventei la care argumentul acestei functii este 180
- rezerva de faza: diferenta dintre argumentul functiei de transfer in bucla deschisa in dreptul frecventei la care modulul acestei functii este 1 si unghiul de 180
Pentru ca sistemul sa fie stabil in bucla inchisa rezerva de amplitudine trebuie sa fie pozitiva (tipic 6-10 dB), respectiv rezerva de faza sa fie pozitiva (tipic 45 -60 ). Procesul prin care se asigura aceste valori (si implicit stabilitatea circuitului) se numeste compensare.
Modul de lucru:
1. Se realizeaza circuitul din Fig.2, cu R=1,5 kΩ, C=33nF, R1=1,5kΩ:
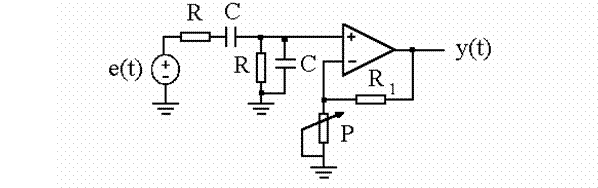
2 Figura 2
- calculati functia de transfer a circuitului, considerand amplificatorul operational ideal.
Aplicam la intrare semnal armonic de la generator. Semnalul de la iesirea circuitului se aplica pe intrarea Y a osciloscopului, iar semnalul de la generator pe intrarea X. Pe ecran va apare o figura Lissajous de forma unei elipse. Se modifica frecventa semnalului pana cand elipsa degenereaza intr-o linie dreapta cu panta pozitiva.
- care este valoarea defazajului intrare-iesire in acest moment?
Fara a mai modifica frecventa se modifica pozitia cursorului potentiometrului pana cand modulul functiei de transfer (amplificarea) devine egal cu 1.
2. In acest moment se indeparteaza generatorul si se realizeaza conexiunea directa intre intrare si iesire. Introducand baza de timp se poate observa pe ecran o oscilatie a carei frecventa se va masura.
- care este frecventa teoretica de oscilatie?
Modificand cursorul potentiometrului se observa ca intr-un sens oscilatia dispare, iar in celalalt sens se mentine, dar iesirea amplificatorului operational intra rapid in saturatie. In acelasi timp, frecventa oscilatiei se modifica.
- care este explicatia modificarii frecventei de oscilatie?
- ce ar trebui sa facem pentru ca oscilatia sa fie armonica (iesirea amplificatorului operational sa nu ajunga in saturatie)?
- care este valoarea minima a amplificarii conexiunii de amplificator neinversor pentru ca regimul oscilant sa se amorseze?
3. Se repeta experimentul in cazul circuitului din Fig.3:
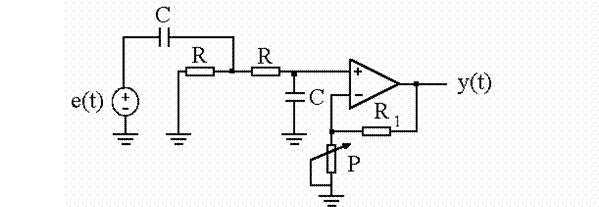
3 Figura 3
- calculati functia de transfer a circuitului, considerand amplificatorul operational ideal.
- care este frecventa teoretica de oscilatie?
Intrebari suplimentare:
1. Propuneti o functie de transfer care sa corespunda unui sistem instabil in bucla inchisa, fapt justificat de aplicarea criteriului Nyquist si care sa se dovedeasca stabil aplicand criteriul Barkhausen.
2. In ce conditii un sistem instabil in bucla deschisa este stabil in bucla inchisa?
3. Cum trebuie sa fie caracteristica de frecventa a unui circuit selectiv plasat in bucla de reactie a unui amplificator neselectiv pentru ca stabilitatea frecventei sa fie buna?
4. Modelati amplificarea amplificatorului operational cu o functie de transfer de ordinul I, de forma: A(s)=A0ω0/s+ω0. Cum se modifica functiile de transfer in bucla deschisa ale circuitelor studiate? Studiati stabilitatea in bucla inchisa a circuitelor cu reactie de mai inainte.