|
|
|
Teoreme ale circuitelor de curent aternativ
Ecuatiile circuitului echivalent cu surse si impedante complexe sunt similare ecuatiilor unui circuit liniar de curent continuu (vezi paragraful 4.7.1). Din acest motiv enunturile teoremelor sunt asemanatoare cu cele din paragraful 2.8 si demonstratiile nu vor fi reluate.
1. Teoremele impedantelor echivalente
Legarea in serie a impedantelor:
. Deoarece Zes = Res + jXes si Zk = Rk + jXk rezulta 
si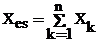 
Legarea in paralel a
impedantelor: 
, deci 
si 
2. Teorema superpozitiei
Fie un circuit de c.a. cu mai multe surse: E1, , El Is,l+1,,Ism. Orice curent (sau tensiune) din circuit se poate scrie ca o suma a curentilor (tensiunilor) din aceeasi latura produsi de fiecare sursa independenta separat, celelalte surse independente fiind pasivizate.
De
exemplu 
unde I1k este curentul produs in latura 1 de sursa independenta din
latura k, celelalte surse independente fiind pasivizate.
Teorema este o consecinta a caracterului liniar al ecuatiilor circuitului. Sursele comandate nu se pasivizeaza.
3. Teoremele generatoarelor echivalente
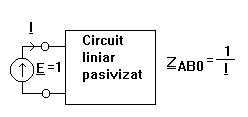
Generatorul echivalent de tensiune al unui dipol Fie un dipol liniar cu bornele A si B.
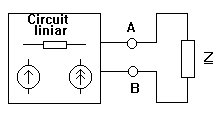
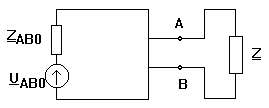
Oricat de complicat ar fi acest circuit el se poate echivala cu un circuit format dintr-o sursa de tensiune UAB0 in serie cu o impedanta ZAB0 unde UAB0 este tensiunea de mers in gol masurata la bornele A si B (impedanta Z fiind scoasa din circuit) si ZAB0 este impedanta echivalenta intre
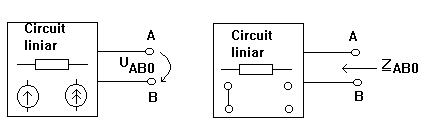
bornele A si B a circuitului pasivizat (sursele comandate nu se pasivizeaza).
Daca circuitul pasivizat este o combinatie serie - paralel de impedante atunci determinarea lui ZAB0 se poate face cu regulile din paragraful 4.7.1. Daca circuitul contine surse comandate sau nu este un circuit serie - paralel, atunci se conecteaza intre A si B o sursa independenta de tensiune de valoare 1V ( sau o sursa independenta de curent de valoare 1A) si ZAB0 rezulta in urma determinarii lui I sau U.
Aplicatie.
Sa se calculeze 
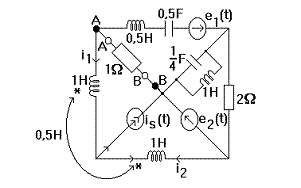
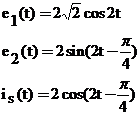
Bobinele cuplate avand un nod comun se poate sparge cuplajul. Prin
pasivizare si calculand impedantele echivalente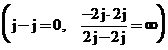 
circuitul capata o
forma mai simpla. Se conec- teaza intre A si B o sursa de tensiune cu 
si rezulta
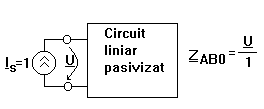
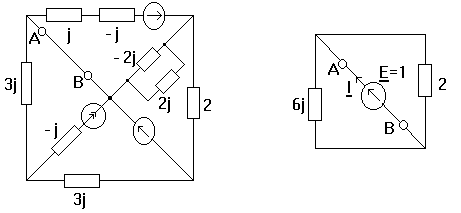
Generatorul echivalent de curent al unui dipol Fie un dipol liniar cu bornele A si B
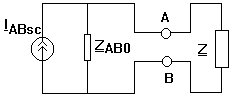
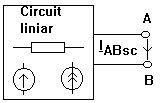
Oricat de complicat ar fi acest circuit el se poate echivala cu un circuit format dintr-o sursa de curent IABsc in paralel cu o impedanta ZAB0 unde curentul IABsc corespunde scurtcircuitului intre bornele A si B.
Daca in schemele echivalente ale diportilor rezistivi liniari (vezi paragraful 2.4.3.3.) se inlocuiesc rezistentele cu impedante si conductantele cu admitante se obtin schemele echivalente ale diportilor de c.a
4. Teorema transferului maxim de putere activa
Se considera o sursa de tensiune electromotoare E si de impedanta interna Zi, la bornele careia se leaga o impedanta Z. Se pune problema urmatoare: ce relatie trebuie sa existe intre Zi si ZAB astfel incat pentru un E dat puterea activa absorbita de Z sa fie maxima.
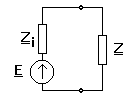
Fie Zi = Ri + jXi si Z = R + jX . Curentul din circuit este 
si deci puterea activa
absorbita de Z este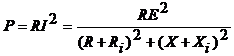 
Se observa ca functia P(R,X) are
un maxim in raport cu X pentru X= -Xi . Valoarea acestui maxim este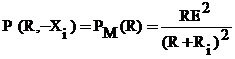 
. Maximul functiei 
are loc pentru R=Ri (vezi
teorema transferului de putere in curent continuu - paragraful 2.4.4.). Rezulta
ca puterea activa absorbita de sarcina
este maxima daca Z = Zi (teorema transferului maxim de putere
activa).
Daca Z = Zi puterea activa Pd cedata de sursa este consumata in cantitati egale de R si Ri deci randamentul circuitului este h=P/ Pd=0,5.
Observatii
i) daca R si/sau X atunci h 1 dar P 0
ii) daca in loc de sursa de tensiune avem o sursa de curent cu parametrii Is si Zi impedanta de sarcina Z absoarbe puterea activa maxima tot daca Z = Zi
ii) deoarece generatoarele de curent alternativ au o impedanta interna inductiva, rezulta ca pentru a absorbi o putere activa maxima sarcina trebuie sa aiba un caracter capacitiv.
