|
|
|
Generalitati. Elemente de mecanica actionarilor
1.1Structura generala a unui Sistem Electric de Actionare Comanda si Reglare
Structura subsistemului electromecanic al unui sistem de actionare electrica cuprinde urmatoarele elemente:
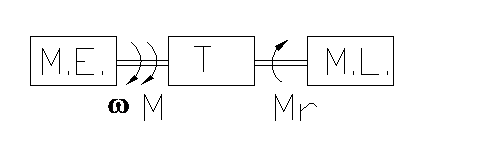
Fig. 1
ME- motorul electric de antrenare, de toate elementele aferente, care transforma energia electrica in energie mecanica;
T- transmisie mecanica- avand rolul adaptarii parametrilor energiei mecanice furnizate de motor la cerintele de actionare ale ML;
ML- masina de lucru.
In functie de procesul tehnologic, ML impune anumite cerinte sistemului de actionare ca:
- natura miscarii - rotatie - continua
- alternativa
- pas cu pas
- translatie- continua
- alternativa
- pas cu pas
- reversibilitatea sensului miscarii;
- reglarea modulului (marimii) miscarii;
- anumite caracteristici de pornire-oprire (inertiala sau cu franare);
- o numita caracteristica
mecanica (
Alegerea corecta a ME si a T se face tinand cont de aceste cerinte, anumite cerinte fiind realizate de ME, iar altele de catre transmisia mecanica T.
Daca ME poate realiza toate cerintele de actionare, T poate lipsi, dar atunci schema electrica trebuie conceputa ca atare.
Prin Sistem de Actionare Electrica (SAE) intelegem ansamblul de dispozitive care transforma energia electrica primita de la retea in energie mecanica si asigura controlul pe cale electrica a energiei mecanice astfel obtinute.
Partile principale ale unui SAE sunt:
- subsistemul de forta - alcatuit din unu sau mai multe motoare electrice si aparatajul electric aferent (aparataj de forta);
- subsistemul de comanda - care modeleaza energia mecanica dezvoltata de motor in concordanta cu cerintele tehnologice ale ML.
Cele mai complexe SAE sunt cele de comanda si reglare.
Structura unui Sistem de Actionare Comanda si Reglare evoluat este urmatoarea:
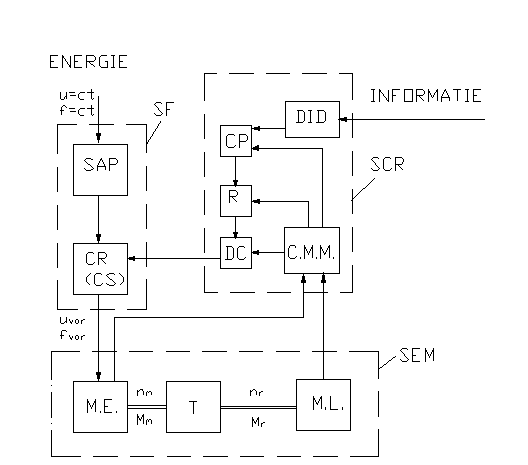
Fig. 2
SF - subsistem de forta (U,I mari);
SAP - subsistem de alimentare si protectie - care realizeaza functiile de conectare -deconectare si de protectie;
CR (CS) - convertizor rotativ (static) - care converteste
parametrii 
, 
in 
, 
;
SCR - subsistem de comanda si reglare;
DID - dispozitiv de introducere a datelor (programarea parametrilor de actionare);
CP - calculator de proces - pentru procesarea informatiei in cadrul sistemului de comanda;
R - regulator - pentru stabilirea caracteristicii de reglare;
DC - dispozitiv de comanda a convertizorului;
CMM - convertorul marimilor masurate - prin care se supravegheaza sistemul in
vederea reglarii parametrilor de actionare.
SEM - subsistemul electromecanic.
1.2. Elemente de mecanica sistemelor de actionare
Indiferent de tipul motorului utilizat, acesta este caracterizat de o
anumita dependenta intre viteza unghiulara 
si momentul
dezvoltat 
, aceasta reprezentand caracteristica mecanica
a motorului: 
.
Daca: 
, unde este momentul motor,
iar 
- momentul rezistent, atunci
dependenta reprezinta caracteristica
mecanica statica (in regim stationar).
Caracteristicile mecanice ale motorului constituie unul din criteriile de baza pentru alegerea acestora, ele aratand daca motorul raspunde cerintelor de pornire, de variatie a vitezei cu sarcina, de comportare la socurile de sarcina impuse de masina de lucru, etc.
Caracteristica mecanica naturala corespunde functionarii motorului in
conditiile pentru care a fost proiectat. Ea se obtine prin
alimentarea motorului la tensiunea nominala 
, la frecventa nominala 
, fara rezistente sau impedante
suplimentare incluse in circuitul inductor sau indus, folosind conexiunile
normale. Ea este unica.
Caracteristicile mecanice artificiale - se obtin cand cel putin un parametru de lucru variaza fata de valoarea nominala; rezulta o infinitate de caracteristici care, in functie de parametrul care se modifica, pot fi:
- reostatice
- de tensiune
- de flux
- de frecventa
Dupa forma curbei caracteristice (legea de variatie
), caracteristicile mecanice statice ale motoarelor pot fi de trei feluri.
a) Caracteristica mecanica
rigida (curba 1, Fig.3), sau de tip sincron, caracterizata
prin 
, indiferent de sarcina (in limitele de
functionare).
Fig. 3
Panta curbei:
Ea se exprima in 
prin relatia:
Se considera caracteristici rigide pentru: 
.
Puterea motorului este proportionala cu sarcina:
Ea apare la motoarele sincrone si la cele pas cu pas.
b) Caracteristica mecanica statica semirigida (curba 2, Fig. 3), sau de tip derivatie avand ca puncte caracteristice:
- 
- punct de
functionare in gol ideal 
.
- 
- punct nominal de
functionare 
, 
(variatie
mica).
Caracteristica este o dreapta inclinata cu panta:
, avand valori in intervalul 
.
Se intalneste la:
- motorul de curent continuu cu excitatie independenta sau derivatie;
- motorul asincron trifazat;
- motorul Diesel.
Deoarece variaza
putin cu , puterea poate fi considerata proportionala
cu cuplul:
c) Caracteristica mecanica statica elastica (curba 3, Fig. 3) sau de tip serie.
Turatia scade neliniar cu cresterea sarcinii.
In general se accepta o variatie de forma:
-
hiperbolica: 
-
parabolica: 
Pentru variatia hiperbolica se poate scrie:
, unde 
si 
si rezulta 
pentru care:
- panta 
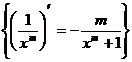
- puterea 
Pentru variatia parabolica se poate scrie:
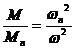, de unde rezulta
pentru care:
- panta 
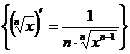
- puterea 
, deci puterea este variabila.
Caracteristica serie se intalneste la:
- motoarele de curent continuu cu excitatie serie;
- motoarele de curent alternativ cu excitatie serie;
- motorul cu aprindere prin scanteie.
Deoarece marea majoritate a motoarelor sunt rotative, se va considera mai intai acest caz (Fig. 4):
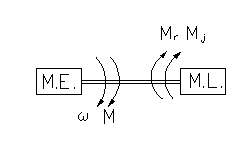
Fig. 4
Considerand
(variabila), energia
cinetica a maselor in miscarea de rotatie se calculeaza
cu formula:
, 
- moment de inertie
Puterea dinamica ( variatia in timp a 
) este:
, de unde 
, in care 
este cuplul dinamic
(inertial).
Ecuatia fundamentala de miscare este data de ecuatia de echilibru a cuplurilor
motor si rezistent 
, rezulta:
,
unde este cuplul rezistent
static din partea masinii de lucru.
In cazul general
, deci momentul de inertie variaza in timp (prin
redistribuirea maselor), sau cu viteza
unghiulara, sau cu unghiul de pozitie 
.
Daca:
, rezulta:
,
deci ecuatia fundamentala capata forma:
,
cu urmatoarele cazuri particulare:
a)
daca , rezulta 
, pentru care se obtine
ecuatia fundamentala in
regim static.
b)
dacacreste, 
, se obtine 
, rezulta faza si cuplu de accelerare.
c)
daca scade, 
, se obtine 
, rezulta faza si cuplu de franare.
a) Cuplul
static rezistent poate fi de
natura:
- reactiva - se opune intotdeauna miscarii, derivat din: - forte de aschiere;
- frecari;
- deformatii plastice.
- potentiala - pastreaza sensul independent de sensul de deplasare, care determina fie accelerare fie franare, derivat din: - campul gravitational (greutati proprii);
- deformatii elastice.
b) Momentul de inertie se calculeaza cu relatia:
, unde 
- distanta de la
centrul de masa la axa de rotatie.
Daca
nu apar redistribuiri de masa, atunci 
, unde 
reprezinta momentul
de gravitatie (sau momentul de volant), indicat in cataloagele
masinilor electrice.
c) Durata procesului tranzitoriu
Procesul este tranzitoriu atat timp cat viteza variaza. Orice proces tranzitoriu este delimitat de doua regimuri stationare.
Presupunand si 
, ecuatia fundamentala are forma:
Daca:
la 
avem 
(regimul
stationar 1),
iar la 
avem 
(regimul
stationar 2),
atunci durata tranzitiei se calculeaza cu relatia:
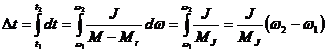
La pornire:
, rezulta 
- timpul de
accelerare
La franare:
, rezulta 
- timpul de
tranzitie
La oprire: 
, rezulta 
- timpul de franare
Deci, durata proceselor
tranzitorii este cu atat mai mare cu cat 
este mai mic si
invers.
In cazul miscarii liniare (de translatie), considerand marimile echivalente:
(forta) 
(viteza liniara)
(masa) 
(deplasarea liniara)
se obtine ecuatia fundamentala de miscare, de forma:
,
unde 
(
-acceleratia liniara)
1.4. Raportarea cuplurilor rezistente statice si a momentelor de inertie la acelasi arbore
Ecuatia fundamentala de miscare s-a
dedus in ipoteza ca toate componentele sistemului au aceeasi
viteza unghiulara. In realitate, datorita transmisiei 
, componentele sistemului au viteze unghiulare diferite. De
aceea este necesara raportarea cuplurilor rezistente statice si a
momentelor de inertie la acelasi arbore.
Aceasta presupune determinarea unor marimi echivalente care sa aiba acelasi efect ca si marimile reale. De obicei raportarea se face la arborele masinii electrice.
Pentru raportare se aplica principiul conservarii energiei: puterea dezvoltata de marimile raportate trebuie sa fie egala cu puterea ceruta de marimile reale, tinandu-se seama si de pierderi.
1.4.1.Raportarea miscarilor de rotatie la miscarea de rotatie
Fie
o transmisie cu roti dintate avand 
arbori (inclusiv
arborele 
si al 
).
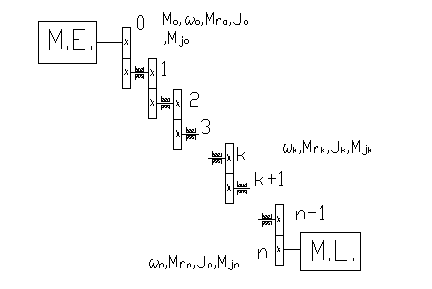
Fig.5
Lucrul mecanic elementar (in
intervalul de timp 
) la arborele k poate fi scris:
, unde
dAkr' - lucrul
mecanic elementar pentru invingerea cuplului static rezistent 
;
dAkj' - lucrul
mecanic elementar pentru invingerea cuplului dinamic 
.
Daca tinem cont de randamentul transmisiei intre motor si arborele k: hk<1, atunci lucrul mecanic elementar dezvoltat de motor pe arborele k devine:
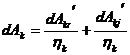
Considerand intreaga transmisie, lucrul mecanic elementar dezvoltat de motor in intervalul de timp dt pe toti arborii va fi:
,
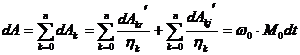unde: M0- cuplul la arborele motor
Dar: 
si 
.
Daca: 
rezulta 
si deci 
.
Inlocuind, expresia dA devine:
, din care rezulta
Deoarece raportul de
transmitere al miscarii de la arborele motor pana la arborele k
este: 
deci 
, rezulta 
astfel ca relatia devine:
Notand : 
si 
, ecuatia fundamentala de miscare se poate
scrie sub forma:
, in care
- momentul rezistent
static redus la arborele motorului;
- momentul
de inertie redus la arborele motorului.
1.4.2. Raportarea miscarii de translatie la miscarea de rotatie
Este necesara cand antrenarea se realizeaza de la un motor rotativ, dar masina de lucru are organe mobile in miscare de translatie.
Se considera organul
mobil de masa m deplasandu-se cu viteza liniara 
. Reducerea la axul
motorului presupune considerarea unui corp fictiv de moment de inertie si viteza
unghiulara , care are aceeasi energie cinetica.
Deci:
de unde rezulta 
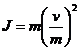
Tinand cont si de randament relatia devine:
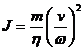
Pentru p corpuri in miscare de translatie, se obtine:
.
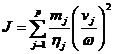Pentru p corpuri in translatie si n+1 corpuri in rotatie:
.
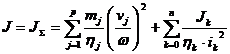Sunt mai rare cazurile cand este necesara raportarea rotatiei la translatie sau a translatiei la translatie, care se realizeaza pe baza principiilor prezentate mai sus.
Observatie: Momentul
axial de inertie are un rol
foarte important in procesele tranzitorii ale sistemului de actionare. El
are doua componente:
momentul
axial de inertie intern al motorului electric - 
(momentul de
inertie al rotorului);
momentul
de inertie extern, datorat celorlalte elemente (de la masina de
lucru, transmisie) reduse la axul motorului - 
.
Factorul
de inertie , 
, al unui sistem de actionare (ML-T-ME) se
defineste prin relatia:
1.5. Stabilitatea statica a sistemelor de actionare (SAE)
Functionarea
in regim permanent (stationar) a unui SAE este caracterizata de
inegalitatea dintre cuplul motor si cel rezistent redus la arborele motor:
Aceasta egalitate se
realizeaza cand , caz in care 
.
Regimul
permanent are caracteristic un punct de functionare (A), care
corespunde intersectiei caracteristicii mecanice a motorului cu caracteristica
mecanica a masinii de lucru 
.
In functie de forma acestor caracteristici, el poate fi un punct stabil sau instabil de functionare.
Un
SAE functioneaza stabil
intr-un punct A, corespunzator unui regim permanent, daca atunci cand apare o perturbatie
mica si cu variatie lenta, fie din partea ME fie din partea
ML, ansamblul ME-T-ML intra intr-un regim tranzitoriu (de variabila)
si se stabilizeaza la o noua valoare intr-un alt punct A2 corespunzator
unui nou regim permanent.
Perturbatiile se pot datora variatiei:
cuplului rezistent Mr;
tensiunii de alimentare;
frecventei.
Daca
la aparitia unei perturbatii, nu tinde spre o
noua valoare stationara, sau sufera oscilatii
neamortizate in jurul valorii anterioare, functionarea in punctul
respectiv este instabila.
Daca perturbatiile au o variatie lenta, se vorbeste despre o stabilitate (sau instabilitate) statica.
Fie caracteristica
motorului si caracteristica masinii de lucru (fig. 6) la
intersectia carora se obtine punctul static de
functionare A1(ω1,M1) pentru
care 
, 
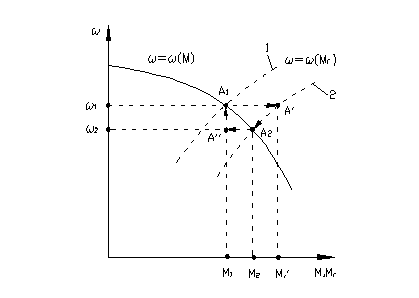
Fig. 6
Presupunand o perturbatie din partea masinii de lucru, care trece de la caracteristica 1 la caracteristica 2, caracteristica motorului ramanand aceeasi, punctul de functionare se muta din A1 in A' pentru care M1<M'r.
Momentul dinamic
, deci ω
scade pana in punctul de fuctionare A2(ω2,M2)
pentru care avem din nou M2=Mr2, deci un nou regim
stationar la 
.
La
disparitia perturbatiei, se revine in punctul A1 pe
traseul A2-A''-A1 in care avem din nou regimul
stationar initial 
. Se spune ca
functionarea SAE este stabila in punctele A1 si A2.
Sa presupunem un alt caz in care caracteristica motorului are panta pozitiva, reprezentata in fig.7.
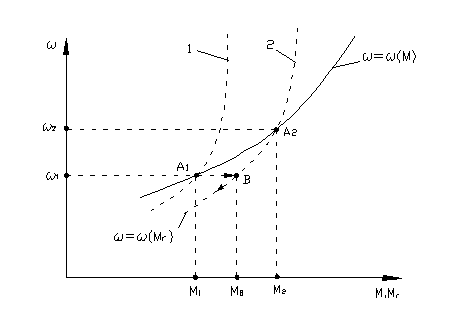
Fig. 7
La aparitia unei perturbatii la masina de lucru (trecerea de la caracteristica 1 la caracteristica 2) punctul de functionare se muta din A1(ω1,M1) in B(ω1,MB).
Deoarece:
M1-MB<0, va scadea, deci
punctul de functionare din B coboara pe curba 2 fara a mai
intersecta din nou caracteristica motoare, deci nu se mai atinge un nou regim
stationar. Ca sa se ajunga in A2 ar trebui ca turatia
sa creasca, lucru imposibil deoarece MB <M2, deci va scadea
pana la oprirea miscarii. In acest caz functionarea este
instabila!
Explicatia este
urmatoarea: la scaderea vitezei, cuplul motor scade mai repede decat cel
rezistent pe curba 2, astfel ca scade si mai mult
pana la oprire; nu mai este posibila egalitatea M=Mr, deci atingerea
unui nou regim permanent.
Din punct de vedere matematic un regim stabil de functionare respecta conditia:
, adica in punctul A panta curbei motorului trebuie
sa fie mai mica decat panta caracteristicii masinii de lucru.
Asadar, vom avea:
- punct
stabil, pentru 
- punct
instabil, pentru 
Pentru
, conditia de stabilitate devine 
deci caracteristica
motorului trebuie sa fie cazatoare.
Observatie:
Daca 
si 
rezulta 
, sau daca perturbatiile au variatii rapide in
timp, este necesar un studiu de stabilitate dinamica.
