
|
|
|
FILTRE ANALOGICE REALIZATE CU COMPONENTE DISCRETE (FILTRE DE TIP K-CT SI DERIVATE "m")
Un filtru analogic poate fi privit ca un cuadripol (doua borne de intrare si doua de iesire) alcatuit din diferite elemente de circuit, care are un comportament diferit fata de semnalele cu diferite frecvente. Cand spunem comportament, diferit ne referim la modul in care filtrul actioneaza asupra marimii (amplitudinii) semnalelor cu diferite frecvente, sau asupra marimii (amplitudinii) componentelor din spectrul de frecvente al semnalului de la intrare. In functie de modul in care filtrele actioneaza asupra semnalelor aplicate la intrare, ele pot fi clasificate in:
filtre "trece-jos" ("taie-sus"), care lasa semnalele cu frecvente pana la o anumita valoare (frecventa de taiere) sa treaca neatenuate, sau atenuate foarte putin, iar pe cele cu frecvente superioare frecventei de taiere le atenueaza foarte puternic.
filtre "trece-sus" ("taie jos"), care sunt complementare filtrelor "trece-jos". Ele atenueaza drastic semnalele cu frecvente mai mici decat frecventa de taiere si lasa sa treaca neatenuate, sau atenuate foarte putin, semnalele cu frecvente superioare frecventei de taiere.
filtre "trece-banda" care lasa sa treaca neatenuate, sau atenuate foarte putin, semnalele cu frecvente cuprinse intr-un anumit domeniu de frecvente, numit banda de trecere, si atenueaza drastic semnalele cu frecvente aflate in afara benzii de trecere.
filtre "opreste-banda", care sunt complementarele filtrelor "trece banda". Ele atenueaza drastic semnalele cu frecvente cuprinse intr-un anumit domeniu de frecvente, numit banda de taiere si lasa sa treaca neatenuate, sau atenuate foarte putin, semnalele cu frecvente aflate in afara benzii de taiere.
In functie de componenta constructiva a filtrelor analogice ele pot fi clasificate in.
filtre pasive, alcatuite numai din elemente pasive de circuit (rezistori, bobine, condensatori). Consecinta unei astfel de structuri este aceea ca amplitudinea semnalului de la iesirea filtrului nu poate fi mai mare decat amplitudinea semnalului de la intrarea lui. Cu alte cuvinte, valoarea maxima a functiei de transfer nu poate fi supraunitara.
filtre active, care reprezinta o combinatie de filtre pasive si elemente active de circuit (de cele mai multe ori, amplificatoare operationale). Prezenta elementelor active (si a eventualelor circuite de reactie) asigura, pe de o parte o amplificare a semnalelor cu frecvente aflate in banda de trecere si pe de alta, o imbunatatire a caracteristicilor filtrului.
Filtre pasive
Cele mai simple filtre pasive sunt cele construite doar din doua elemente: rezistor + condensator sau rezistor + bobina, conectate ca in Fig.1. Ele se mai numesc si celule elementare de filtrare sau filtre de ordinul 1, putand fi doar de tipul "trece-jos" sau "trece-sus", in functie de pozitia celor doua elemente in circuitul care reprezinta filtrul. Sa observam ca rezistorul este prezent in toate cele patru combinatii posibile de filtre. Filtrele in care bobina, respectiv condensatorul, ocupa aceeasi pozitie in circuit sunt complementare: daca unul este de tip "trece-jos", celalalt este de tip "trece-sus". Fiind circuite de tip cuadrupol, comportamentul filtrelor poate fi caracterizat cu ajutorul diagramelor Bode: caracteristica de transfer in tensiune si caracteristica de faza. Prima ne da informatii despre tipul filtrului, iar cea de a doua ne spune care este defazajul semnalului de la iesire fata de semnalul aplicat la intrare.
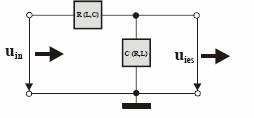
Fig.1
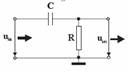
Modalitatea de calcul a parametrilor caracteristici ai unui filtru elementar este foarte simpla, mai ales atunci cand elemntele de circuit se considera ca fiind ideale. Vom exemplifica pe un filtru RC, a carui schema este prezentata in Fig.2. Pentru simplificarea si mai mult a calculelor, vom considera ca filtrul lucreaza in conditiile cele mai bune: in domeniul util de frecvente, impedanta filtrului este mult mai mare decat impedanta de iesire a sursei de semnal si mult mai mica decat impedanta sarcinii pe care el debiteaza energie.
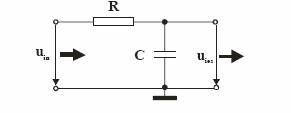
Fig.2
Aplicand medoda de calcul cu marimi complexe, functia de transfer in tensiune va avea expresia:
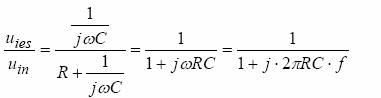 (1)
(1)
iar modulul ei:
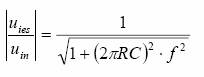 (2)
(2)
Din expresia
(2) se vede imediat ca daca 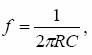 atunci
atunci 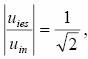 ,
ceea ce inseamna o atenuare cu 3 dB a semnalului de iesire
fata de semnalul de intrare. Vom "boteza" aceasta
frecventa particulara cu fT (frecventa
de taiere), relatia (2) putand fi acum scrisa:
,
ceea ce inseamna o atenuare cu 3 dB a semnalului de iesire
fata de semnalul de intrare. Vom "boteza" aceasta
frecventa particulara cu fT (frecventa
de taiere), relatia (2) putand fi acum scrisa: 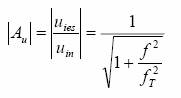 (3)
(3)
Reprezentarea grafica a functiei de transfer (3) a filtrului este prezentata in Fig.3a. Ea "ne spune" ca este vorba despre un filtru "trece-jos", care lasa sa treaca prin el semnalele cu frevnete mai mici decat fT si atenueaza foarte mult semnalele cu frecvente mai mari.
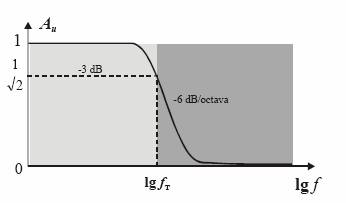
Fig.3a
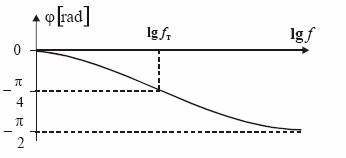
Fig.3b
Pentru a vedea cum actioneaza filtrul asupra fazei semnalului, vom rationaliza expresia functiei de transfer astfel incat ea sa poata fi scrisa sub forma Re + jIm:
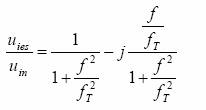 (4)
(4)
Astfel, defazajul semnalului de iesire fata de cel de intrare va avea expresia:
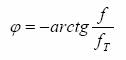 (5)
(5)
Din reprezentarea grafica a caracteristicii de faza (Fig.3b) se poate observa ca, pe tot domeniul de frecvente, tensiunea de iesire este defazata in urma tensiunii de intrare. Rezultatul acesta putea fi prevazut si fara calculul functiei de transfer, observand ca tensiunea de iesire este chiar tensiunea de la bornele condensatorului, care, pentru a se incarca pana la o anumita valoare a tensiunii, are nevoie de un interval de timp finit, determinat de capacitatea sa si de valoarea rezistentei prin care se incarca.
Si comportarea filtrului la limitele domeniului de frecvente poate fi analizata fara cunoasterea formei analitice a functiei de transfer, cunoscand comportarea elementelor reactive de circuit (in cazul de fata un condensator) in curent continuu si la frecvente foarte mari. Astfel:
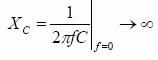 in curent continuu condensatorul poate fi
inlocuit cu o intrerupere ⇒
in curent continuu condensatorul poate fi
inlocuit cu o intrerupere ⇒
si
![]() la frecvente
foarte mari condensatorul poate fi inlocuit cu un scurcircuit ⇒
la frecvente
foarte mari condensatorul poate fi inlocuit cu un scurcircuit ⇒
Tinand seama de aceste doua adevaruri, pot fi desenate schemele echivalente ale filtrului din Fig.2 la limita curentului continuu si la limita frecventelor foarte inalte (Fig.4).
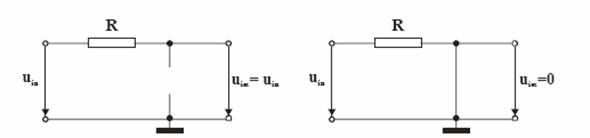
la limita curentului continuu si frecvente mici la limita frecventelor foarte mari
Fig.4
Se vede imediat ca la limita curentului continuu si la frecvente mici (probabil pina la o anumita valoare) semnalul trece spre iesire, pentru ca la frecvente mari sa fie puternic atenuat (chiar pana la 0).
Este evident ca aceasta este o metoda aplicabila doar pentru o evaluare calitativa a comportarii unui circuit continand elemente reactive (condensatori, bobine) la cele doua extreme ale valorii frecventei. Ce se intampla insa intre aceste aceste extreme poate fi prezis doar pe baza analizei functiei de transfer. In cazul analizat mai sus filtrul contine doar doua elemente de circuit si modulul functiei de transfer este monoton descrescator odata cu cresterea frecventei. Daca circuitul reprezentand filtrul are trei componente sau mai multe, este posibil ca pe intreg domeniul de frecvente functia de transfer sa aiba mai multe maxime si/sau minime si chiar sa ia de mai multe ori valoarea zero. In aceste situatii se vorbeste despre polii si zerourile functiei de transfer.
In Tabelul 1 sunt prezentate valorile modulului functiei de transfer (3) pentru cateva valori particulare ale frecventei.
Tabelul1
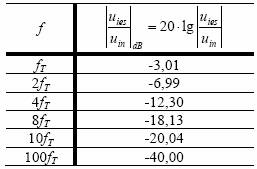
Dupa cum se poate observa, pentru frecventa mai mari decat 2fT, la fiecare dublare a frecventei atenuarea semnalului de iesire creste cu aproximativ 6dB. De asemenea, pentru frecvente mai mari decat 10fT, la fiecare multiplicare cu 10 a frecventei atenuarea semnalului de iesire creste cu masura pantei functiei de transfer in vecinatatea frecventei de taiere. Alaturi de tipul de filtru si de frecventa de taiere, panta filtrului este o alta caracteristica a lui. Astfel, despre filtrul elementar RC analizat anterior se spune ca are o panta de - 6 dB/octava sau - 20 dB/decada.
Similar cu analiza filtrului RC pot fi analizate si celelalte filtre simple. Sinteza comportarii celor patru filtre elementare de ordinul I este prezentata in Tabelul 2.
Tabelul 2
SCHEMA
Au
ϕ[rad]
DIAGRAME BODE
filtru RC "trece-jos"
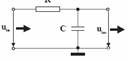
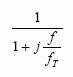
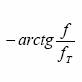

filtru CR "trece-sus"
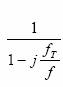
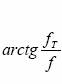

filtru RL "trece-sus"
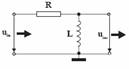
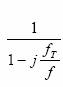
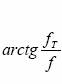

filtru LR "trece-jos"
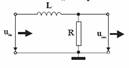
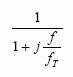
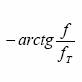

Observatie. In toate cazurile au fost neglijate elementele parazite: pierderile in dielectricul condensatorului, rezistenta de pierderi a conductorului bobinei si capacitatile dintre spirele bobinei. Caracteristicile filtrului vor suferi modificari mai mari sau mai mici in functie de ponderea acestor elemente intr-un caz concret.
Se observa ca din combinatiile posibile de cate doua elemente pe care s-a analizat mai sus lipseste combinatia LC (bobina + condensator). Acest caz trebuie tratat separat deoarece, fiind vorba de doua elemente de circuit reactive si complementare, orice combinatie a lor (serie sau paralel) reprezinta un circuit rezonant, cu un comportament particular la frecventa de rezonanta. Dintre cele doua combinatii vom analiza mai detaliat doar circuitul LC paralel din trei motive: a) este cel mai utilizat; b) este mai greu de calculat si c) la frecvente ridicate, o simpla bobina reprezinta ea insasi un circuit rezonant. In general, filtrele LC se folosesc in domeniul frecventelor inalte si foarte inalte (sute de kilohertzi sau mai mari).
Filtre drivate m
Filtre de tip K-ct prezinta doua inconveniente:
impedanta variaza cu frecventa
atenuarea in afara benzii nu este suficienta pentru diferite aplicatii.
Filtrele cu structura m - derivate se obtin din filtre de tip K-ct, astfel obtinandu-se:
a) minimizarea impedantei
b) atenuarea in afara benzii, mica.
Pentru circuitul considerat:
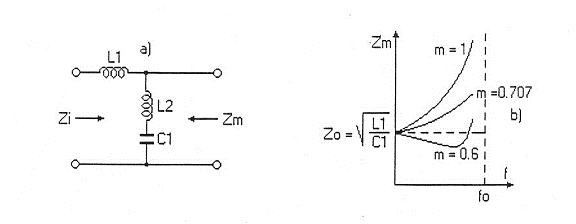
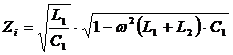
![]()
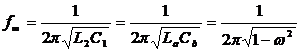
S-a
definit frecventa ![]() pentru un filtru
derivat " m" , T.J.
pentru un filtru
derivat " m" , T.J.
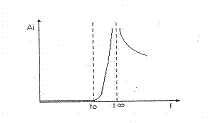
Variatia atenuarii pentru un filtru derivat "m"'
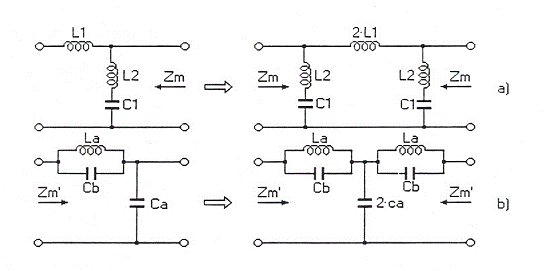 Sunt
prezentate in continuare structuri de filtre derivate "m"
Sunt
prezentate in continuare structuri de filtre derivate "m"
Fitre derivate "m"
sectine ᴦ sectiune ![]()
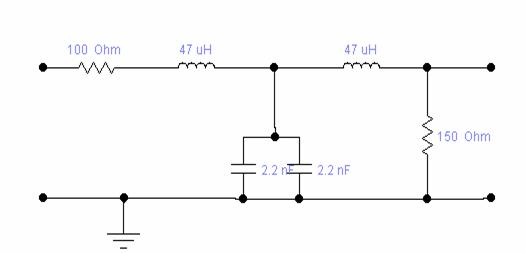
Modul de lucru
Aparate necesare: - generator de semnal
- osciloscop
- sursa de alimentare
f [kHz]
V0
V0/Vref
20logV0/Vref
100
400
450
800
900
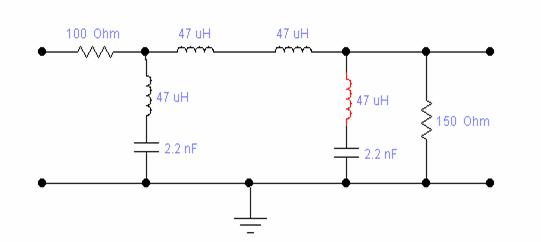
f [kHz]
V0
V0/Vref
20logV0/Vref
100
400
450
800
900
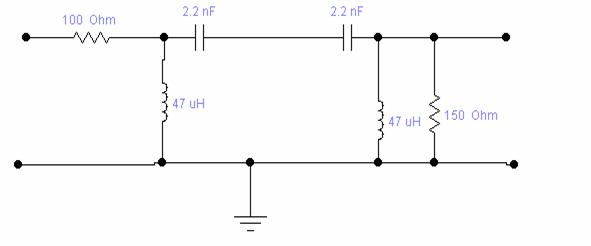
f [kHz]
V0
V0/Vref
20logV0/Vref
1000
600
590
200
100
Rgen
= 500 ![]()
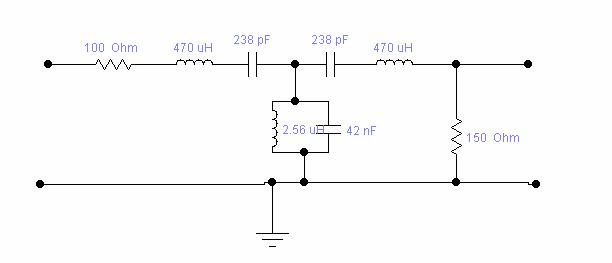
f [kHz]
V0
V0/Vref
20logV0/Vref
350
360
690
700
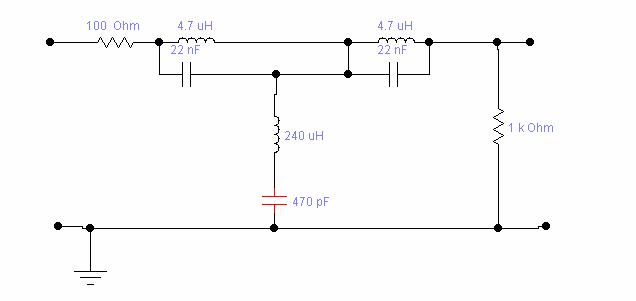
f [kHz]
V0
V0/Vref
20logV0/Vref
350
360
690
700
1000
1