|
|
|
Caracterizarea materialelor conductoare
Conductoarele sunt materiale la care conductivitatea
electrica, 
, depaseste valoarea de 108 (Wm)-1. Ele se pot clasifica dupa mai multe criterii.
Dupa tipul de purtatori de sarcina:
cu conductivitate electronica;
cu conductivitate ionica.
Din prima categorie fac parte metalele, grafitul etc., iar din a doua electrolitii (solutii ale acizilor, hidratilor si sarurilor etc.). Conductivitatea celor din urma este mult mai mica decat a primelor.
Dupa starea de agregare:
conductoare solide;
conductoare lichide - metale topite si electroliti;
conductoare gazoase - gaze in stare de plasma.
Dupa valoarea conductivitatii si dependenta ei de temperatura:
conductoare obisnuite;
supraconductoare.
Modelul clasic al cnductiei in metale se bazeaza pe conceptul de nor electronic format din electroni liberi care se misca haotic printre atomi in volumul de material, fara un sens anume. Concentratia de electroni liberi este de ordinul 1022 cm-3, de acelasi ordin cu cea a atomilor. Daca dintr-un motiv oarecare apare o concentratie locala de sarcina electrica diferita de cea din vecinatate, atunci in foarte scurt timp, de ordinul 10-17 10-18s, ea se uniformizeaza si concentratia devine constanta. Prin urmare, metalele se caracterizeaza prin neutralitate electrica in orice volum de material. Miscarea haotica a electronilor este de natura termica si viteza termica este de ordinul 105 107m/s.
Prin aplicarea unui camp electric E asupra materialului conductor, apare o miscare dirijata a electronilor in sens opus campului, numita viteza de drift:
(2.1)
unde factorul 
se numeste
mobilitatea electronului.
La inceput miscarea electronilor este uniform accelerata, dar in scurt timp se ajunge la viteza de saturatie egala cu viteza de drift. Limitarea vitezei dirijate este produsa de ciocnirile electronilor mobili cu atomii ficsi ai retelei cristaline a metalului. Modelarea matematica a conductiei este descrisa in continuare.
Forta electrostatica produsa de campul E determina o acceleratie a electronilor:
(2.2)
unde 
este masa electronului iar 
sarcina sa electrica.
Viteza maxima atinsa in momentul unei ciocniri este:
(2.3)
Viteza medie (viteza de drift) este:
(2.4)
Din (2.1) si din (2.4) se obtine mobilitatea electronilor:
(2.5)
Densitatea de curent de conductie este:
(2.6)
unde 
este versorul
directiei campului electric iar 
concentratia de
electroni liberi.
Conductivitaea electrica (respectiv
rezistivitatea, 
) este:
(2.7)
Valoarea medie a
timpului dintre doua ciocniri se poate considera, intr-o prima
aproximatie, ca timp de relaxare, 
. Atunci se poate defini conductivitatea astfel:
(2.8)
O descriere mai precisa a fenomenului conductiei in metale precum
si dependenta lui de temperatura se
gasesc in [1].
Din cauza agitatiei termice a atomilor, distanta medie dintre doua ciocniri succesive scade, timpul mediu de relaxare scade, viteza de drift si conductivitatea scad. Cresterea rezistivitatii cu temperatura se poate exprima simplu printr-o relatie de forma:
(2.9)
Unde 
este rezistivitatea la temperatura T0 iar 
Rezistivitatea catorva metale la temperatura obisnuita (300K) este data in tabelul urmator.
Tabelul 2.1
|
Metal |
Na |
Cu |
Ag |
Ca |
Al |
Cr |
W |
Fe |
Ni |
Pt |
|
r[10-8Wm] |
4.75 |
1.70 |
1.61 |
3.60 |
2.74 |
12.9 |
5.3 |
9.8 |
7.0 |
10.4 |
Dependenta rezistivitatii de temperatura ese mai complexa decat ecuatia (2.9) si se poate evidentia grafic in fig. 2.1.
Se pot evidentia 5 zone de dependenta a rezistivitatii cu temperatura.
Zona I este zona de supraconductibilitate specifica temperaturilor foarte coborate. Unele metale au zona de supraconductibilitate continua pana la 0K (linia punctata) altele, cele supraconductoare au rezistivitate practic nula incepand de la o temperatura TC.
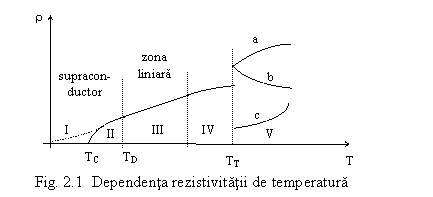
Zona
II se caracterizeaza printr-o
crestere rapida a rezistivitatii cu temperatura
(proportionala cu T5), dupa care urmeaza o
zona liniara specifica temperaturilor obisnuite, in care
este valabila ecuatia (2.9). Ea incepe in punctul TD
(temperatura Debye) si reprezinta acea temperatura la care
vibratiile mecanice (fononii) au frecventa maxima 
. Valoarea sa este data de ecuatia:
(2.10)
Unde h este constanta lui Plank iar k constanta lui Boltzman.
In zona a IV-a se constata o dependenta mai redusa de temperatura, pentru ca in zona V sa apara un salt al rezistivitatii corespunzator temperaturii de topire a metalului.
