
|
|
|
Rezonanta dipolilor
1. Definitii si exemple
Exista doua definitii ale rezonantei: prima se foloseste in electroenergetica, a doua se utilizeaza la circuitele electronice.
Definitia 1 Un dipol de c.a. este la rezonanta daca absoarbe pe la borne o putere reactiva nula,
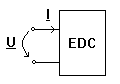
adica Qabs=UI sinj = 0.
Deci la rezonanta defazajul j dintre U si I este nul (sinj = 0 T j = 0). Daca impedanta echivalenta la bornele dipolului este Z=R+jX, Q=XI =0 TX = 0 deci la rezonanta reactanta echivalenta este nula si dipolul are o comportare rezistiva la borne.
Definitia 2 a) Se considera la bornele dipolului o sursa de tensiune cu pulsatie variabila si valoare efectiva constanta.. Pulsatiile de rezonanta sunt cele pentru care I(w) are maxime si minime.
Exemplu
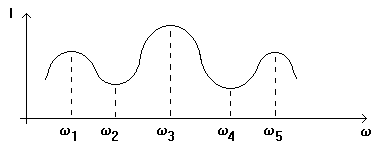
- dipolul este la rezonanta pentru pulsatiile w1 w2 w3 w4 w5
- in cazul maximelor de curent (w1 w3 w5 ) avem rezonanta de tensiune,
- in cazul minimelor de curent (w2 w4) avem rezonanta de curent.
Se observa ca deoarece I = Y U si U = ct, curba Y (w) are aceeasi alura cu I (w
b) Se considera la bornele dipolului o sursa de curent cu pulsatie variabila si valoare efectiva constanta.. Pulsatiile de rezonanta sunt cele pentru care U(w) are maxime si minime.
Exemplu
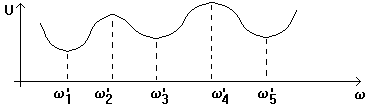
- dipolul este la rezonanta pentru pulsatiile w'1 w'2 w'3 w'4, w'5
- in cazul minimelor de tensiune (w'1 w'3 w'5) avem rezonanta de tensiune,
- in cazul maximelor de tensiune (w'2 w'4) avem rezonanta de curent.
Deoarece U = Z I si I = ct, curba Z(w) are aceeasi alura cu U(w
Observatii
i) cele doua definitii ale rezonantei nu duc in general la aceleasi pulsatii de rezonanta
ii) rezonanta de tensiune are loc la pulsatiile pentru care Y(w) are maxime locale si deci Z(w)=1/ Y(w) are minime locale
iii) rezonanta de curent are loc la pulsatiile pentru care Y(w) are minime locale si deci Z(w)=1/ Y(w) are maxime locale.
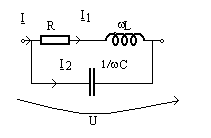
Exemple. a)
![]()
Se
calculeaza puterea aparenta complexa S = UI* si se anuleaza
puterea reactiva obtinandu-se pulsatiile de rezonanta dupa definitia 1: 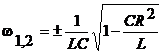
![]() ; se observa ca daca R 0
; se observa ca daca R 0
atunci w2 ![]() . Se calculeaza minimele si maximele lui I(w)
respectiv ale lui Z(w
. Se calculeaza minimele si maximele lui I(w)
respectiv ale lui Z(w
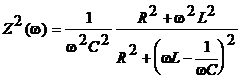 si
si ![]() are solutiile
are solutiile 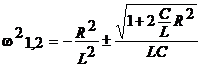
(daca R 0
atunci w2 ![]() ). Pulsatiile de rezonanta obtinute dupa cele doua definitii
nu sunt aceleasi.
). Pulsatiile de rezonanta obtinute dupa cele doua definitii
nu sunt aceleasi.
b) Impedanta complexa a
circuitului RLC serie este ![]() . Rezulta
. Rezulta
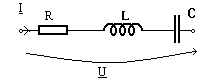
![]() . Dupa prima definitie, pulsatia de rezonanta corespunde lui
X=0 deci
. Dupa prima definitie, pulsatia de rezonanta corespunde lui
X=0 deci ![]() . Dupa a doua definitie, se calculeaza
. Dupa a doua definitie, se calculeaza ![]() si se obtine aceeasi
valoare pentru w0 . Daca U=ct in raport cu w,
la rezonanta I ia valoarea maxima deoarece Z ia valoarea minima Z(w0)=R.. Pentru acest circuit Uc(w0)=|Xc|I= UL(w0)=|XL|I si Uc(w0)= -UL(w0) deci U(w0)=UR(w0) +UC(w0) + UL(w0)=UR(w0). Este posibil ca la rezonanta
si in jurul pulsatiei de rezonanta UC si UL sa aiba
valori mai mari decat tensiunea U a sursei de alimentare. Se noteaza cu
si se obtine aceeasi
valoare pentru w0 . Daca U=ct in raport cu w,
la rezonanta I ia valoarea maxima deoarece Z ia valoarea minima Z(w0)=R.. Pentru acest circuit Uc(w0)=|Xc|I= UL(w0)=|XL|I si Uc(w0)= -UL(w0) deci U(w0)=UR(w0) +UC(w0) + UL(w0)=UR(w0). Este posibil ca la rezonanta
si in jurul pulsatiei de rezonanta UC si UL sa aiba
valori mai mari decat tensiunea U a sursei de alimentare. Se noteaza cu 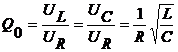 factorul de calitate
al circuitului unde UL, UC, UR se considera la
rezonanta. Daca Q0 >1 (
factorul de calitate
al circuitului unde UL, UC, UR se considera la
rezonanta. Daca Q0 >1 (![]() ), tensiunea bobinei si cea a condensatorului depasesc
tensiunea sursei de alimentare.
), tensiunea bobinei si cea a condensatorului depasesc
tensiunea sursei de alimentare.
c) Circuitul RLC
paralel are propietati selective in frecventa duale celui RLC serie. 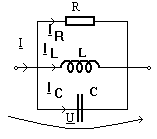
Utilizand ambele
definitii se obtine aceeasi pulsatie de rezonanta a acesui circuit ![]() . La rezonanta
. La rezonanta 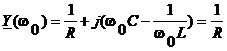 deci Y are valoarea
minima. Daca U=ct in raport cu w, la rezonanta I ia valoarea
minima deoarece I=YU. Pentru acest circuit Ic w0)=U/|Xc|= IL(w0)=U/|XL| si Ic w0)= -IL(w0) deci I(w0)=IR(w0) +IC(w0) + IL(w0)=IR(w0). Este posibil ca la rezonanta
si in jurul pulsatiei de rezonanta IC si IL sa aiba
valori mai mari decat curentul I prin sursa de alimentare. Se noteaza cu Q0
factorul de calitate
deci Y are valoarea
minima. Daca U=ct in raport cu w, la rezonanta I ia valoarea
minima deoarece I=YU. Pentru acest circuit Ic w0)=U/|Xc|= IL(w0)=U/|XL| si Ic w0)= -IL(w0) deci I(w0)=IR(w0) +IC(w0) + IL(w0)=IR(w0). Este posibil ca la rezonanta
si in jurul pulsatiei de rezonanta IC si IL sa aiba
valori mai mari decat curentul I prin sursa de alimentare. Se noteaza cu Q0
factorul de calitate 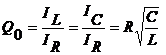 unde IL, IC,
IR se considera la rezonanta. Daca Q0 >1
(
unde IL, IC,
IR se considera la rezonanta. Daca Q0 >1
(![]() ),curentul bobinei si al condensatorului depasesc curentul
total.
),curentul bobinei si al condensatorului depasesc curentul
total.
2. Aplicatii tehnice ale rezonantei
a)Compensarea factorului de putere Presupunem ca avem o linie de transport al energiei electrice la capatul careia este conectat consumatorul inductiv (asa cum sunt majoritatea consumatorilor energetici) din figura a..
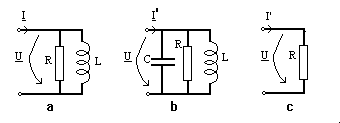
Curentul absorbit de
consumator este :![]() deci
deci 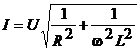 si cosj =
si cosj =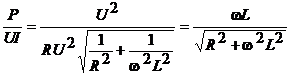 .
.
Se conecteaza un condensator in
paralel cu consumatorul astfel incat ![]() (circuitul b). In
acest caz avem un circuit RLC derivatie la rezonanta a carui impedanta de
intrare este Z=R si curentul absorbit de receptor este
(circuitul b). In
acest caz avem un circuit RLC derivatie la rezonanta a carui impedanta de
intrare este Z=R si curentul absorbit de receptor este ![]() . Puterea reactiva absorbita de consumatorul inductiv in
paralel cu condensatorul C este nula, si pierderile de putere activa pe linia
de transport (de rezistenta r ) vor fi minime : DP'linie = rI'2 < DPlinie=
rI2. In acest caz factorul de
putere cosj'=1 si avem o compensare
totala a factorului de putere.
. Puterea reactiva absorbita de consumatorul inductiv in
paralel cu condensatorul C este nula, si pierderile de putere activa pe linia
de transport (de rezistenta r ) vor fi minime : DP'linie = rI'2 < DPlinie=
rI2. In acest caz factorul de
putere cosj'=1 si avem o compensare
totala a factorului de putere.
Consumatorii industriali nu au tot
timpul aceiasi parametri (se opresc anumite utilaje, in anumite zile nu se
lucreaza, etc). Pentru a nu se ajunge la functionarea in regim capacitiv (care
produce efecte nedorite in sistem) mentinand pierderile de putere pe linie la un
nivel rezonabil se face o compensare
partiala a factorului de putere (de exemplu cosj'=0,92).
In acest caz calculul capacitatii condensatorului care se leaga in paralel cu
consumatorul inductiv se face astfel: diferenta intre puterea reactiva
absorbita de consumatorul necompensat Q=UIsinj si cea absorbita de
consumatorul compensat partial Q'=UIsinj' este absorbita de condensator
(QC=wCU2). Exprimand
puterile reactive in functie de puterea activa P absorbita de consumator (Q=Ptgj,
Q'=Ptgj') rezulta ![]() ; in acest calcul se considera ca U nu se modifica prin
conectarea condensatorului.
; in acest calcul se considera ca U nu se modifica prin
conectarea condensatorului.
b) Montaje Boucherot
Se considera cele doua circuite din figura de mai jos. Daca parametrii bobinei si condensatorului indeplinesc conditia de rezonanta (w2 LC = 1) atunci curentul prin impedanta Z are valoarea U/wL pentru primul circuit si UwC pentru al doilea circuit, deci este independent de valoarea lui Z .
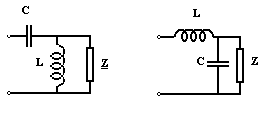
Aceasta proprietate se poate verifica foarte usor.
c)Circuite de rezistenta constanta
Impedanta de intrare intr-un astfel de circuit nu depinde de frecventa, desi circuitul contine si elemente reactive. Cele doua circuite din figura de mai jos au Z=R atunci cand parametrii
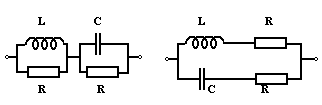
indeplinesc conditia: R2 = L/C. Verificarea acestei propietati este un exercitiu simplu.