Analiza circuitelor de cale fara joante cu extremitati de atenuare

Analiza circuitelor de cale fara joante cu extremitati de atenuare

In cadrul analizei circuitelor de cale fara joante izolante ca baza se foloseste teoria generala a circuitelor de cale dar se tine seama de cateva trasaturi specifice conditionate de lipsa joantelor izolante.

Analiza circuitelor de cale fara joante cu extremitati de atenuate se face in cele trei regimuri de lucru ale functionarii lor, urmarind transmisia curentului intre sursa de alimentare (emisie) si receptie (releu), in situatia cea mai defavorizabila (situatia limita) pentru fiecare regim in parte.

Regimul normal

Pentru circuitul de cale echilibrat, in regim normal , ecuatiile de transfer pentru linia de lungime l- , sunt:

chγ(l- shγ(l-

shγ(l- chγ(l-

Luand in consideratie si ecuatiile de transfer ale liniei de lungime cuplata cu bucla rezulta urmatoarele ecuatii de transfer pentru circuitul de cale de lungime l:

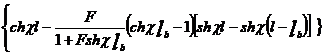
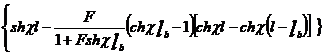
=sh

sh

fig II.3. Schema echivalenta a circuitului de cale cu extremitati de atenuare in regim normal

Linia electrica fiind infinit lunga in ambele extremitati ale circuitului de lungime l, rezulta:

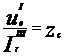
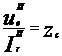
Pentru circuitul de cale echilibrat , aplicand semnalul de control dintr-un generator de tensiune rezulta urmatoarea expresie pentru admitanta de transfer in regim normal:

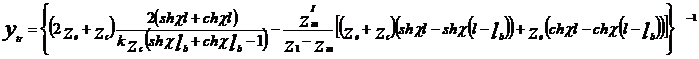
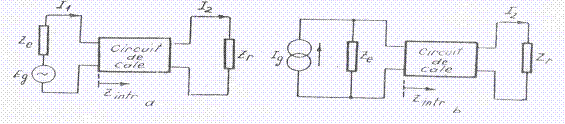
fig. II. 4 - Circuit de cale cu semnalul de control aplicat:

a - un generator de tensiune,

b - dintr-un generator de curent

In cazul aplicarii semnalului de control dintr-un generator de curent fig II.4 b functia de transfer in curent are expresia:

Pentru cazul , aproximand functiile hiperbolice cu primiii termeni ai dezvoltarii in serie, rezulta:

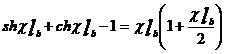
In aceste aproximatii admitanta de transfer in regim normal devine:

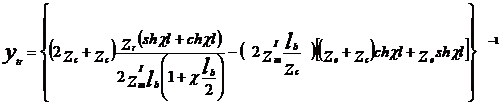
Rezulta pentru impedanta de intrare in circuitul de cale in regim normal urmatoarea expresie

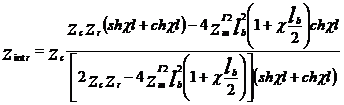
Regimul de sunt

In urmatoarea figura este prezentata achema echivalenta a circuitului de cale cu extremitati de atenuare excitat prin generator de tensiune, in prezenta unui sunt aflat la distanta W de extremitatea de receptie, in conditiile cele mai defavorabile din punct de vedere al valorii conductantelor traverselor ( , , ).

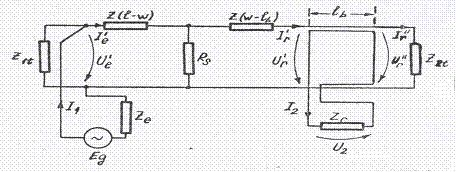
fig.II.5 - Schema echivalenta a circuitului de cale cu extremitati de atenuare, excitat din generatorul de tensiune, in regim de sunt

Impedantele si se datoresc fie impedantelor de intrare (finite pentru frecventa de lucru) a emitatoarelor si receptoarelor circuitelor de cale vecine, fie suntarii circuitelor de cale vecine catre vehiculele care le ocupa.

Pentru valorile specificate ale conductantelor transversale, in cazul circuitului de cale echilibrat, relatiile caracterizand linia cuplata cu bucla devin:

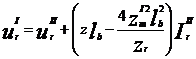
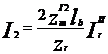
Expresia pentru admitanta de transfer a circuitelor de cale cu extremitati de atenuare in regim de sunt, cu semnal de control aplicat dintr-un generator de tensiune este urmatoarea:

+

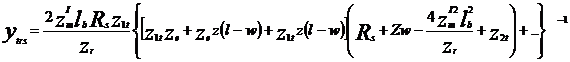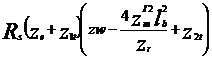
Din punct de vedere al valorilor impedantelor si (care pot varia prin schimbarea pozitiei vehiculului pe circuitelor de cale vecine) cazul critic, adica valoarea maxima a modulului admitantei de transfer, corespunde pentru:

circuitul de cale vecin cu extremitatea emisie liber;

circuitul de cale vecin cu extremitatea receptie ocupat cu un vehicul cu sunt perfect aflat la extremitatea buclei de cuplaj

In aceste conditii valoarea admitantei de transfer devine:

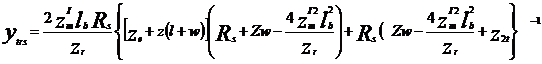
Pentru cazul aplicarii semnalului de control dintr-un generator de curent functia de transfer in curent rezulta

Cap III MODELAREA SI SIMULAREA CIRCUITELOR DE CALE FARA JOANTE

Circuitul de cale fara joante poate fi considerat ca fiind o linie multifilara avand doua conductoare active in prezenta solului.

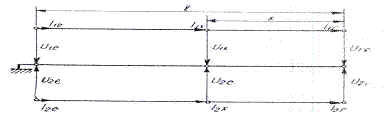
Fig. III. 1 Circuitul de cale fara joante privit ca linie de transmisie multifilara, cu doua conductoare active in prezenta solului.

Pentru frecventele uzuale de lucru ale circuitului de cale fara joante capacitatile specifice partiale sunt neglijabile. In aceste conditii ecuatiile telegrafistilor de ordinul unu pentru circuitul de cale se prezinta astfel:

Cunoscand constantele de integrare, se pot scrie relatiile ce definesc valorile tensiunilor si curentilor in orice punct al liniei functie de marimile de iesire. Astfel pentru se obtin marimile de intrare:

Aceste relatii pot fi scrise si sub forma matriciala:

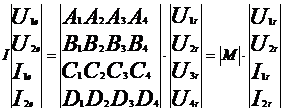
Relatiile de mai sus definesc un hexapol echivalent caii fara joante, caraterizat prin matricea |M|. Matricea |M|, functie de parametrii primari ai liniei si de lungime, stabileste o relatie biunivoca intre marimile de intrare si de iesire din linie, considerata ca hexapol. Dar, practic, nu intereseaza explicit valorile tensiunilor si curentilor in circuitele sina-pamant, ci valorile tensiunilor si curentilor in circuitul format din cele doua sine, la capatul caruia sunt conectate aparatele de emisie si receptie. Apare deci necesitatea determinarii parametrilor unui cuadripol echivalent circuitului de cale fara joante, care sa tina seama de caracterul specific de hexapol al caii.

Determinarea parametrilor cuadripolului echivalent

Schema echivalenta a circuitului de cale fara joante cuprinde hexapolul caii, intre punctul de emisie si cel de receptie, definit prin matricea |M|, admitantele reflectate din circuitul de cale adiacent capatului de receptie Ya, Yb, Yc, respectiv capatului de emisieYA, YB, YC , si aparatajul reprezentat printr-un generator de tensiune de impedanta interna, Ze si impedanta de intrare a receptorului Zr.

Intre punctele 1-1' si 2-2' circuitul de cale fara joante se prezinta ca un cuadripol de parametri A, B, C, D. Determinarea parametrilor presupune stabilirea unei relatii intre marimile de intrare, Ue, Ie, si marimile de iesire Ur, Ir, tinand seama de configuratia circuitului cuprins intre aceste puncte.

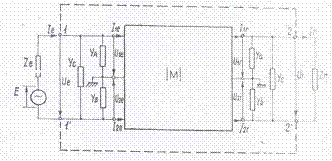
Fig. III.2 Schema echivalenta a circuitului de cale fara joante.

Relatiile de dependenta ce definesc cuadripolul echivalent sunt:

Coeficientii cuadripolului echivalent sunt:

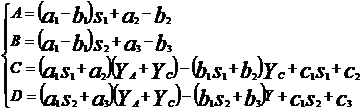
Aceste relatii reprezinta forma cea mai generala a coeficientilor cuadripolului caii, cu ajutorul carora se poate determina comportarea circuitului de cale fara joante in orice situatie existenta in exploatare. Particularizindu-le, de exemplu pentru cazul unui circuit de cale fara joante echilibrat, se obtin coeficientii cuadripolului caii:

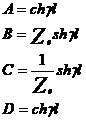
Unde impedanta caracteristica Zc si constanta de propagare γ au expresiile:

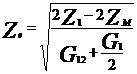
Utilizand cele doua fire ale caii drept conductoare electrice se pot transmite informatii intre blocuri ale instalatiei automatizate, sau prin cuplaj magnetic, catre vehicule, informatii tinand de siguranta circulatiei sau auxiliare (ultima functie fiind practic abandonata pentru instalatii noi).

Pentru studiul circuitelor de cale fara joante izolante ca baza se foloseste teoria generala a circuitelor de cale dar se tine seama de cateva trasaturi specifice conditionate de lipsa joantelor izolante.

Schema generala echivalenta a circuitului de cale fara joante izolante este prezentata in figura de mai jos.

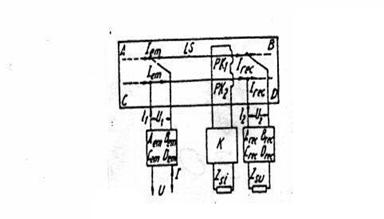
Fig.III. 3 Schema generala echivalenta a circuitului de cale fara joante izolante

Aceasta schema, la fel ca si schema circuitului de cale cu joante izolante este compusa din montajul in cascada a trei cuadripoli: Em, Rec si Ls. Cuadripolii Em si Rec inlocuiesc aparatura respectiva de alimentare si a capetelor de relee, iar cuadripolul Ls inlocuieste linia de cale ferata.

Acest cuadripol se deosebeste substantial de cuadripolul din schema cu joante izolante. Din cauza aceasta, pentru analiza si sinteza circuitelor de cale ferata fara joante izolante, este necesara deducerea ecuatiei pentru calculul coeficientilor cuadripolului, care substituie linia. In circuitele de cale nelimitate preluarea sarcinii se realizeaza atat ca tensiune respectiv curent. In cadrul preluarii sarcinei ca intensitate a curentului, releul de cale intra in functiune in contul fortei electromotoare, introdusa in linii de curenti I, I in bobinele de linie PK1 si PK2, asezate la sine. Pentru circuitele de cale de acest gen, o mare importanta o au problemele legate de asigurarea sensibilitatii la sunt prin aplicarea la circuitul de cale a doua sunturi de tren cu rezistenta diferita in ambele parti ale punctului de conectare a sarcinii.

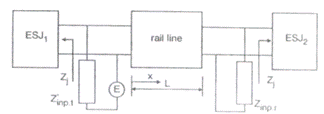
Fig. III..10 Modelul circuitului de cale fara joante

In figura de mai sus este reprezentat modelul circuitului de cale fara joante, unde Z'imp t si Z'imp r reprezinta valorire impedantei echipamentelor din capetele de emisie respective receptie ale circuitului de cale. Diferenta fata de celelalte tipuri de circuite de cale o reprezinta existenta joantelor electrice de separatie ESJ1 si ESJ2

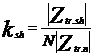
unde,

Impedanta de transfer a circuitului de cale este raportul dintre sursa de tensiune si curentii de la cele doua capete de receptie ale circuitului.

An, Bn, Cn, Dn, Ash, Bsh, Csh, Dsh sunt coeficientii celor doua capete de recetie ale circuitului atat in cazul cand acesta prezinta ocupat ( regim normal) cat si in situatia cand este ocupat ( regim de sunt).

Acesti coeficienti se determina folosind urmatoarele formule:

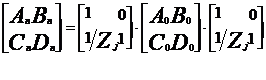
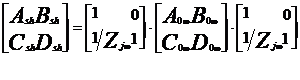
unde,

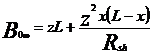
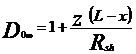
sunt constante caracteristice impedantei si propagarii in circuitul de cale in regim normal

Zj este impedanta de intrare in joanta electrica de separatie in cazul rezistentei de balast minime.

Z este impedanta sigura pentru lungime de 1 km

Rsh este rezistenta de sunt a trenului,

x este pozitia de sunt a trenului.

este impedanta de intrare in joanta electrica de separatie la valoarea rezistentei de balast de

N este coeficientul variatiei sursei de tensiune (1,5)

Conditia de detectare a trenului pe circuitul de cale este realizata cand

Conditia aceasta este necesara dar nu si suficienta in cazul cind trenul se afla in zona joantei electrice

Sensibilitatea la sunt din zona joantei electrice de separatie se verifica folosind conditia prezentata anterior.

Regimul de sunt are urmatorii coefienti:

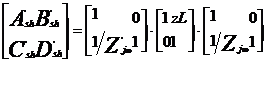
unde,

este impedanta de intrare in joanta, avand si suntul aflat la distanta x de locul de conectare ala echipamentului de transimie (capatul de emisie)

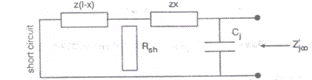
Fig . III.11 Impedanta de intrare in joanta electrica de separatie in cazul cand

Pentru reducerea atenuarii liniilor circuitului se folosesc condensatori de compensare. Valoarea optima kilometrica a condensatorilor de compensare se afla cu ajutorul formulei Heaviside .

In acest caz avem formula:

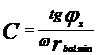
unde, este unghiul de faza al impedantei iar este frecventa unghiulara

Se folosesc diferite valori ale capacitatii condensatorilor montati intre firele caii. Astfel in Franta se folosesc condensatori de 40 montati la fiecare 100 m iar in Rusia se folosesc condensatori de aceeasi valoare dar se amplaseaza la distante de 250 m.

Modelul circuitului de cale compensat se prezinta in figura de mai jos:

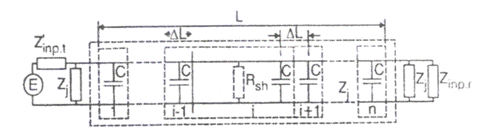
Fig. III.12 Circuitul de cale compensat

Pentru a clarifica influenta capacitatilor de compensare se foloseste un model complicat de circuit Intre capetele circuitului, se conecteaza o retea ce in elemente avind capacitatea C asezate in mijlocul firelor caii.

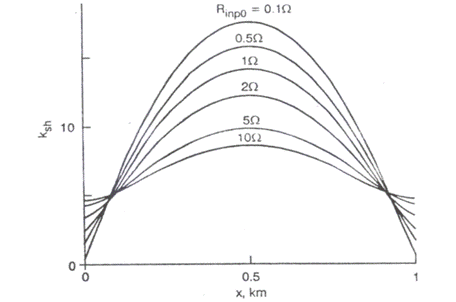
Fig. III.13. zona de sensibilitate a suntului

Exemple de aplicatii in cazul circuitelor de cale fara joante, necompensate

Circuite de cale fara joate, fara compensare

Se prezinta modelul matematic la care circuitul de cale are L=1 km, frecventa f=2300 Hz, Rsh=0,06Ω, r bal min=1Ω.km si l = 20 m, impedanta pe kilometru este

Capacitatea echivalenta necesara acordarii joantei este

Consideram impedanta de intrare si de iesire ca sunt egale si unghiul de faza fiind zero,

Rezultatele valorilor sensibilitatii la suntare si distributia acestora la capetele circuitului sunt prezentate in figura de mai jos

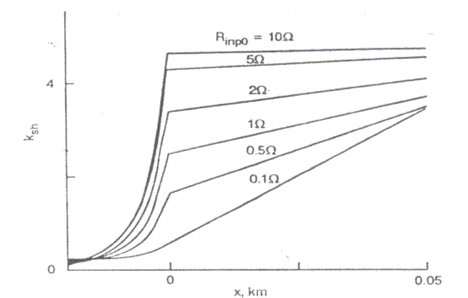
Fig . III.14 Sensibilutatea de suntzare in zona joantei

Formele de distributie a sensibilitatii la suntare a circuitelor de cale fara joante nu au diferente esentiale in zona de capat a acestora.

In partea de mijloc a circuitului sensibilitatea la suntare scade odata cu cresterea rezistentei la capete acestuia. Daca rezistentele la capete circuitului sunt egale, senibilitatea la suntare la punctele x=0 si x=L este la fel de scazuta cand intre capetele circuitului se aplica Rimp0.

Valoarea minima a sensibilitatii la suntare creste daca cresc valorile lui R inp0.

Sensibilitatea la suntare scade o data cu cresterea lungimii circuitelor de cale fara joante.

Circuite de cale fara joate, cu compensare

Evaluarea influentei condensatorilor de compensare se face utilizand urmatoarele valori:

f=2300Hz, L=1,5km, Rsh=0,06Ω, r bal min=1Ω.km si l = 20 m. Capacitatea kilometrica se calculeaza pentru condensatori avand C'=693μF. Pe fiecare kilometru sunt n condensatori de capacitate C, valoarea fiecarui condensator fiind C'/n

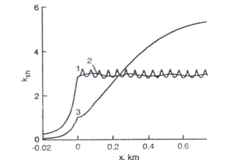
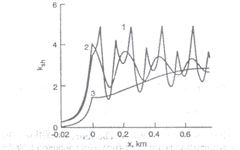
Curba 1 din figura de mai jos reprezinta distributia sensibilitatii la suntare calculata pentru

si trei valori diferite ale lui n.

Sensibilitatea la suntare a circuitului de cale fara joante cu compensare distribuita este inclusa pentru comparare (curba 2)

Curba 3 reprezinta sensibilitatea la suntare pentru circuitele necompensate.

Pentru studiu se prezinta prima parte a circuitului. Cea de-a doua parte este simetrica, se considera impedantele de inceput si de sfarsit ca fiind egale.

In figura de mai se observa efectul condensatorilor de compensare asupra sensibilitatii de suntare a circuitului de cale.

Sensibilitatea la suntare este este distribuita dupa o functie periodica complexa, cu perioade egale avand pasi de marime ΔL. Cand condensatoarele de compensare sunt mai putine se functioneaza cu oscilatii mai inalte.

Cand numarul condensatoarelor este destul mare, curba 1 coincide cu curba 2.

Mai multe condensatoare de compensare fac sa cresca sensibilitatea la sunt in apropierea capetelor circuitului si sa scada in zona centrala astfel incat se stabilizeaza sensibilitatea la sunt in intreg circuitul. Sensibilitatea la sunt in apropierea joantei este de asemenea sporita.

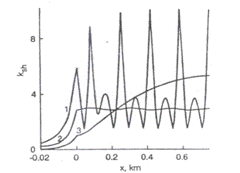
a.

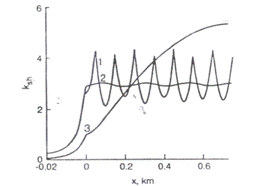
b.

c.

Fig. III.15 Distributia sensibilitatii la suntare in circuitele de cale compensate, pentru diferite numere de condensatori pe kilometru (a n = 6, Rinp0 = 2Ω, b n = 10, Rinp0 = 2Ω ,c n = 20, Rinp0 = 2Ω

Numarul de condensatoare pe kilometru este foarte important.

In figura de mai jos raportul Z tr.n/Z tr.n fata de n, unde Z tr.n este impedanta de transfer in regim normal de lucru cu compensare.

In aceasta figura se observ ca imbunatatirea atenuarii se realizeaza cu cel putin opt condensatori pe kilometru. Mai multi condesatori slabesc atenuarea dar crestera numarului n peste 10-15 duce la o ineficienta economica. Mai putin de opt condensatori pe kilometru duce la un efect negativ privind rara de atenuare

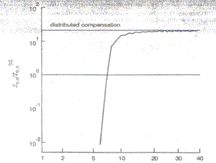
Fig. III. 16 Atenuarea in functie de numarul codensatorilor

a.

b.

c.

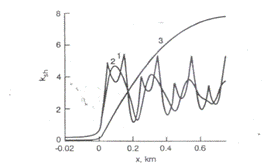
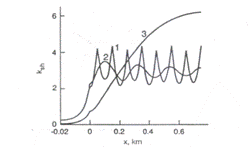
Fig. III.17 Distributia senibilitatii la sunt in circuitul de cale compensat pentru diferite valori ale rezistentei de intrare (a n = 10, Rinp0 = 0,1Ω, b n = 10, Rinp0 = 5Ω ,c n = 10, Rinp0 = ∞)

Influenta valorii rezistentei Rinp0 se poate compara cand curbele de sensibilitate pentru n=10 si patru valori ale Rinp0 sunt prezentate

Se observa usor ca efectul rezistentelor de la capete circuitele de cale cu compensare distribuita este mult mai scazut decat pentru circuitele de cale necompensate (curba 3).

Cand valorile Rinp0 sunt foarte mari sau foarte mici sunt indeplinite conditiile de aparitie ale curbei 2

Oscilatiile inalte semifica deteriorarea sensibilitatii la suntare pentru niste puncte din linie.

Pentru a preintampina acest lucru trebuie indeplinita conditia :

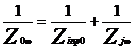
unde este impedanta caracteristica distribuita in linia ferata compensata pentru

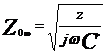
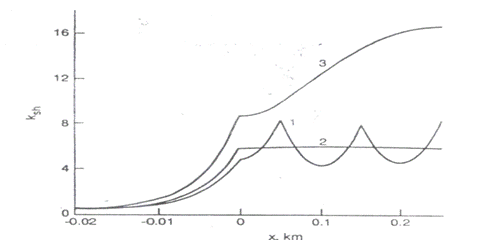
Fig. III. 18 Sensibilitatea la suntare pentru un circuit de cale compensat , scurt

In figura de mai sus sunt prezentate trei cube cu n=10 si Rinp0 = 2Ω dar cu lungimea L= 0,5 km.

Se poate observa ca sensibilitatea la sunt in cazul circuitului de cale compensat cu cinci condensatori avand 69,3 μF (curba 1) este mai mica decat in cazul circuitului necompensat (curba 3).

Se observa ca marimea pasilor ΔL ale curbei 1 sunt apropiatide curba 2 dar sensibilitatea la sunt este mai slaba decat la curba 3.

In zona joantei, sensibilitatea la suntare in cazul circuitului compensat este mai slaba decit in cazul circuitului necompensat.

Lungimea maxima a circuitelor de cale fara joante.

Capacitatea circuitului de-a sesiza suntul produs de tren la o anumita distanta nu numai in zona joantei este de baza in a determinarea lungimii maxime a circuitului de cale.

Toate rezultate obtinute pentru circuitele de cale compensate si necompensate arata ca in zona joantei electrice sensibilitatea la suntare are cele mai dificile conditii: scade odata cu cresterea lungimii circuitului.

Folosind algoritmul relatiilor fundamentale se determina lungimile maxime ale circuitelor de cale fara joante

Curba 1 - circuite de cale jara joante compensate

Curba 2 - circuite de cale fara joante cu compensate distribuita

Curba 3 - circuite de cale fara joante fara compensare.

Tabelul nr. 1 Lungimile maxime ale circuitului de cale fara joante (km)

Este obligatoriu ca la receptia circuitului de cale suntat, in cele mai defavorabile conditii, sa nu ajunga energie.

In determinarea lungimii admisibile a circuitului de cale fara joante este de baza indeplinirea conditiei ksf≥1 pentru punctual x = - l/2

In timpul calculelor lungimii circuitului de cale se creste gradual valoarea lui ksh. Daca ksh>1 lungimea circuitului de cale poate sa cresca.

Pentru ksf≥1 sunt indeplinite conditiile de obtinere a lungimii maxime a circuitului de cale fara joante.

Au fost facute calcule pentru cinci valori diferite ale rezistebtei de balast

Au fost determinate pentru fiecare din acestea , valorile condensatorilor de compensare, impedanta de intrare a echipamentelor la receptie Z imp0. Retultatele sunt prezentate in tabelul de mai sus

- Lungimea maxima a circuitului de cale fara joante depinde de valoarea minima a rezistentei de balast si de rezistenta la suntare facuta de tren.

- Pentru o valoare a rezistentei de balast accepata de mai multe administratii feroviare europene lungimea maxima a circuitelor de cale necompensate este mai mare decat in cazul celor compensate. Pentru aceste situatii compensatia se foloseste doar pentru a reduce rata atenuarii.

- In ceea ce priveste lungimea circuitelor de cale compensate, acestea sunt eficiente la valori nai mari ale rezistentei de balast ( rbal min). Aceasta este conditia pentru liniile de mare viteza unde rezistenta minima de balast acceptata este de In acest caz si valorile scazute ale sutului facut de catre tren, pot face ca lungimea circuitului de cale sa cresca semificativ. Cu compensarea nu se obtin rezultate bune si valori inalte ale rezistentei la sunt a trenului.

Lungimile maxime ale circuitelor de cale compensate pot fi determinate cu acuratete pentru sectoare de 100 m.

Incercarea de-a creste lungimea maxima a circuitelor de cale folosind valori de capacitati kilometrice diferite de conditia lui Heaviside duce la atenuari mari si rezultate foarte nesatisfacatoare.

In principiu metoda de verificare utilizata este folosirea de programe diferite de abordare.

De exemplu programul folosit pentru calculul sensibilitatii la suntare pe lungimea circuitului circuitului este diferit de programul folosit pentru zona joantei de separatie.

Punctul de coordonate x=0 este comun pentru doua programe si este bun pentru a detecta erorile.

Numarul de condensatoare de compensare pe sectoare kilometrice pentru tipul de circuit de cale JTC UM 71 este n= 10. In Rusia la circuitele de cale fara joante si rezistenta de intrare aechipamentelor este iar in Germania se utilizeaza cel mai mult si

Rata inalta de a atenuare a liniei pate fi redusa in situatia cand se folosesc condensatoare de compensare.

Pentru valori mari ale rezistentei minime de balast, compensarea duce la cresterea lungimii.

Distanta dinte condensatorii de compensasie nu trebuie sa fie mai mica de 100 m

CIRCUITUL CU ALIMENTARE MEDIANA

REGIMUL NORMAL

Circuitele cade cale fara joante cu alimentare mediana sunt prezentate in figura de mai jos unde este inversul ipmpedantei de intrare comuna emimisiei si respectiv sunt impedantele de intrare la capetele celor doua receptii.

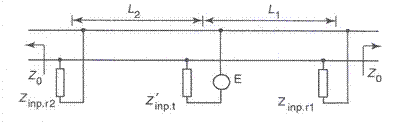
Fig III.19 Circuit de cale fara joante cu alimentare centrala

Cele doua sectiuni de cale cu lungimi L1 si L2 sunt alimentate de la o sursa de putere (E). Impedanta liniei este notata cu Z0 atit pentru sectorul din stinga cit si pentru cel din dreapa locului de amplasare a emisiei.

Pentru a studia sensibilitatea fata de sunt respectiv ruptura caii in sectiunea de lungime L1 se foloseste diagrama echivalenta a circuitului de cale nelimitat

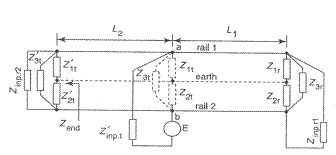
Fig. III.20 Diagrama echivalenta a circuitului de cale fara joante cu alimentare centrala

Impedantele de intrare a conductoarelor infinit lungi formate intre firu 1, firul 2 si pamat pot fi echivalate in notare astfel: si , impedanta de intrare a liniei infinit lungi dintre cele doua sine are expresia . In mod analog impedantele de intrare la punctul de emisie se noteaza , ,

In cazul circuitului de cale simetric se stabilesc urmatoarele ecuatii:

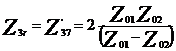
unde si sunt impedantele caracteristice liniei ferate permtru excitare in mod comun respectiv diferential.

Impedanta se poate determina in functie de care in functie de impedanta de intrarea a caii poate fi localizata in punctele a si b

unde,

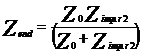iar este constanta de propagare in firele caii in cazul excitarii in mod diferential.

poate fi definit astfel:

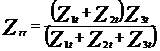
Expresia lui are urmatoarea forma:

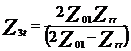
Utilizand transformarea in echivalarea diagramei circuitului de cale se deduc urmatoarele:

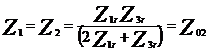
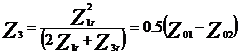
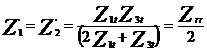
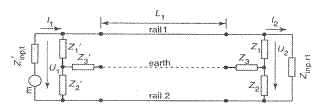
Fig. III.21 Diagrama de transformare echivalenta a circuitului de cale fara joante

Deoarece curentul nu este simetric intre firele caii rezulta ca impedantele si se pot reprezenta folosind ecuatiile in cazul regimului normal.

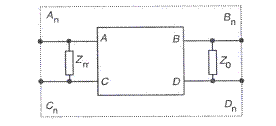
Fig. III. 22 Regimul normal la tipul de circui de cale cu doua receptii

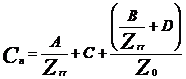
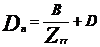
unde,

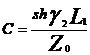
REGIMUL DE SUNT

Coeficientii circuitului de cale fara joante cu alimentare mediana (centrala) in prezenta suntului pozitionat in sectiunea de lujgime L1 pot fi determinati cu ajutorul diagramei circuitului echivalent din figura de mai jos. Se considera valoarea rezistentei de balast ca fiind infinita

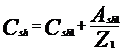
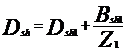
unde,

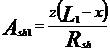
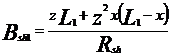
unde z este impedanta kilometrica a firelor caii.

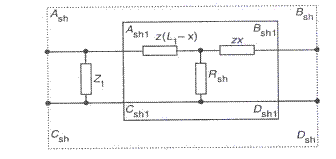
Fig. III.23 Regimul de sunt la tipul de circuit de cale cu doua receptii

Se defineste ca fiind raportul dintre amplitudinea curentului de la receptie inainte si dupa suntare si are urmatoarea expresie:

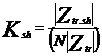
unde,

Regimul de sunt este realizat cand oricare ar fi x:

Regimul de sunt se studiaza pentru a se afla punctul cu sensibilitatea critica.

Distributia sensibilitatii critice a suntului la circuitele de cale fara joante se prezinta in figura de mai jos

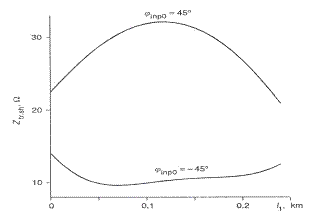
Fig. III.24 Distributia sensibilitatii critice a suntului la circuitele de cale fara joante

Valorile obtinute in cazul prezentat in figura de mai sunt sunt pentru un semnal de frecventa f'= 750Hz,

Coeficientul de dispersie la suprafata p=9.1 L1=L2=0,25 km si